Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-03T20:36:50.899Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification Theory for Valuations of Arbitrary Rank

Published online by Cambridge University Press:  20 November 2018

Murray A. Marshall
Murray A. Marshall*
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout, we consider a finite Galois extension L|K of non-archimedian valued fields which are maximally complete [2, Chapter 2], Let v denote the valuation on L and let L* denote the group of non-zero elements of L. We mayidentify the value group v(L*) of L with a subgroup of D, where D denotes the minimal divisible ordered group containing v(K*). We denote the residue field of L by 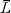, and will always assume that the field extension 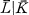is separable. The characteristic of 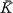will invariably be denoted by p ; much of what follows is trivial in case p = 0.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 4 , August 1974 , pp. 908 - 916
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Artin, E. and Tate, J., Class field theory (Benjamin, New York, 1967).Google Scholar
2. Schilling, O. F. G., The theory of valuations, Math. Surveys No. 4 (Amer. Math. Soc, Providence, 1950).Google Scholar
3. Sen, S., On automorphisms of local fields, Ann. of Math. 90 (1969), 33–46.Google Scholar