Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Campbell, James T
and
Jamison, James E
1991.
The analysis of composition operators on Lp and the Hopf decomposition.
Journal of Mathematical Analysis and Applications,
Vol. 159,
Issue. 2,
p.
520.


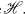 .
. 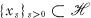 such that
such that