Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-18T10:04:26.161Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudoprime Reductions of Elliptic Curves

Published online by Cambridge University Press:  20 November 2018

C. David  and
J. Wu
C. David
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montréal, QC, H3G 1M8 email: [email protected]
J. Wu
Affiliation:
Institut Elie Cartan Nancy, CNRS, Université Henri Poincaré (Nancy 1), INRIA, 54506 Vandoeuvre-lès- Nancy, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 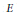$E$ be an elliptic curve over 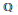$\mathbb{Q}$ without complex multiplication, and for each prime 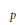$p$ of good reduction, let 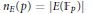${{n}_{E}}(p)\,=\,\left| E\left( {{\mathbb{F}}_{p}} \right) \right|$. For any integer 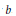$b$, we consider elliptic pseudoprimes to the base 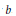$b$. More precisely, let 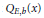${{Q}_{E,B}}(x)$ be the number of primes 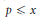$p\le x$ such that 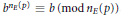${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$, and let 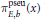$\pi _{E,b}^{\text{pseu}}(x)$ be the number of compositive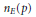${{n}_{E}}(p)$ such that 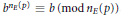${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$ (also called elliptic curve pseudoprimes). Motivated by cryptography applications, we address the problem of finding upper bounds for 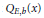${{Q}_{E,B}}(x)$ and 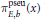$\pi _{E,b}^{\text{pseu}}(x)$, generalising some of the literature for the classical pseudoprimes to this new setting.

Keywords

11N3614H52Rosser-Iwaniec sievegroup order of elliptic curves over finite fieldspseudoprimes
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 1 , 01 February 2012 , pp. 81 - 101
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Balog, A., Cojocaru, A. C., and David, C., Average twin prime conjecture for elliptic curves. Amer. J. Math., to appear.Google Scholar
[2] Cojocaru, A. C., Reductions of an elliptic curve with almost prime orders. Acta Arith. 119(2005), no. 3, 265-289. http://dx. doi. org/10.4064/aa119-3-3Google Scholar
[3] Cojocaru, A. C., Luca, F., and Shparlinski, I. E., Pseudoprime reductions of elliptic curves. Math. Proc. Cambridge Philos. Soc. 146(2009), no. 3, 513-522. http://dx. doi. org/10.1017/S0305004108001758Google Scholar
[4] Crandall, R. and Pomerance, C., Prime numbers. A computational perspective. Second ed., Springer, New York, 2005.Google Scholar
[5] David, C. and Wu, J., Almost prime values of the order of elliptic curves over finite fields. Forum Math., to appear.Google Scholar
[6] Erdʺos, P., On pseudoprimes and Carmichael numbers. Publ. Math. Debrecen 4(1956), 201-206.Google Scholar
[7] Gordon, D. M. and Pomerance, C., The distribution of Lucas and elliptic pseudoprimes. Math. Comp. 57(1991), no. 196, 825-838. http://dx. doi. org/10.1090/S0025-5718-1991-1094951-8Google Scholar
[8] Halberstam, H. and Richert, H.-E., Sieve methods. London Mathematical Society Monographs, 4, Academic Press, London-New York, 1974.Google Scholar
[9] Iwaniec, H., A new form of the error term in the linear sieve. Acta Arith. 37(1980), 307-320.Google Scholar
[10] Jones, N., Almost all elliptic curves are Serre curves. Trans. Amer. Math. Soc. 362(2010), no. 3, 1547-1570. http://dx. doi. org/10.1090/S0002-9947-09-04804-1Google Scholar
[11] Koblitz, N., Primality of the number of points on an elliptic curve over a finite field. Pacific J. Math. 131(1988), no. 1, 157-165.Google Scholar
[12] Kowalski, E., Analytic problems for elliptic curves. J. RamanujanMath. Soc. 21(2006), no. 1, 19-114.Google Scholar
[13] Lagarias, J. C. and Odlyzko, A. M., Effective versions of the Chebotarev density theorem. In: Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, London, 1977, pp. 409-464.Google Scholar
[14] Luca, F. and Shparlinski, I. E., Pseudoprime values of the Fibonacci sequence, polynomials and the Euler function. Indag. Math. (N. S.) 17(2006), no. 4, 611-625. http://dx. doi. org/10.1016/S0019-3577(06)81037-2Google Scholar
[15] Luca, F. and Shparlinski, I. E., Pseudoprime Cullen and Woodall numbers. Colloq. Math. 107(2007), no. 1, 35-43. http://dx. doi. org/10.4064/cm107-1-5Google Scholar
[16] Murty, M. R., Murty, V. K., and Saradha, N., Modular forms and the Chebotarev density theorem. Amer. J. Math. 110(1988), no. 2, 253-281. http://dx. doi. org/10.2307/2374502Google Scholar
[17] Pomerance, C., On the distribution of pseudoprimes. Math. Comp. 37(1981), no. 156, 587-593. http://dx. doi. org/10.1090/S0025-5718-1981-0628717-0Google Scholar
[18] van der Poorten, A. J. and Rotkiewicz, A., On strong pseudoprimes in arithmetic progressions. J. Austral. Math. Soc. Ser. A 29(1980), no. 3, 316-321. http://dx. doi. org/10.1017/S1446788700021315Google Scholar
[19] Luca, F. and Shparlinski, I. E., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent. Math. 15(1972), no. 4, 259-331. http://dx. doi. org/10.1007/BF01405086Google Scholar
[20] Luca, F. and Shparlinski, I. E., Quelques applications du théorème de densité de Chebotarev. Inst. Hautes Études Sci. Publ. Math. 54(1981), 323-401.Google Scholar
[21] Stark, H. M., Some effective cases of the Brauer-Siegel theorem. Invent. Math. 23(1974), 135-152. http://dx. doi. org/10.1007/BF01405166Google Scholar
[22] Zywina, D. J., The large sieve and Galois representations. Ph. D. Thesis, University of California, Berkeley, 2008, arxiv:0812.2222.Google Scholar