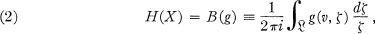Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bergman, Stefan
1963.
On the coefficient problem in the theory of a system of linear partial differential equations.
Journal d'Analyse Mathématique,
Vol. 11,
Issue. 1,
p.
249.
Mitchell, Josephine
1963.
Integral theorems for harmonic vectors in three real variables.
Mathematische Zeitschrift,
Vol. 82,
Issue. 4,
p.
314.
Cima, Joseph
1963.
Some properties of harmonic functions generated by the bergman-whittaker operator.
Annali di Matematica Pura ed Applicata,
Vol. 63,
Issue. 1,
p.
175.
Mitchell, Josephine
1966.
Bounds for Solutions of a System of Linear Partial Differential Equations on Domains with Bergman-Silov Boundary.
Canadian Journal of Mathematics,
Vol. 18,
Issue. ,
p.
1272.
1969.
Function Theoretic Methods in Partial Differential Equations.
Vol. 54,
Issue. ,
p.
297.


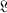 be a closed rectifiable curve, not going through the origin, which bounds a domain Ω in the complex ζ-plane. Let
be a closed rectifiable curve, not going through the origin, which bounds a domain Ω in the complex ζ-plane. Let