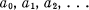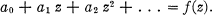Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schoenberg, I. J.
1953.
On smoothing operations and their generating functions.
Bulletin of the American Mathematical Society,
Vol. 59,
Issue. 3,
p.
199.
Aissen, M. I.
1957.
Cyclically Ordered Sets.
Canadian Journal of Mathematics,
Vol. 9,
Issue. ,
p.
406.
Van Rossum, H.
1965.
Totally Positive Polynomials.
Indagationes Mathematicae (Proceedings),
Vol. 68,
Issue. ,
p.
305.
Medgyessy, P.
1972.
On the unimodality of discrete distributions.
Periodica Mathematica Hungarica,
Vol. 2,
Issue. 1-4,
p.
245.
Jurkat, W. B.
and
Peyerimhoff, A.
1972.
On power series with negative zeros.
Tohoku Mathematical Journal,
Vol. 24,
Issue. 2,
Pommerenke, Ch
1973.
Padé approximants and convergence in capacity.
Journal of Mathematical Analysis and Applications,
Vol. 41,
Issue. 3,
p.
775.
Wynn, P.
1975.
Upon a class of functions connected with the approximate solution of operator equations.
Annali di Matematica Pura ed Applicata,
Vol. 104,
Issue. 1,
p.
1.
De Bruin, M.G.
1976.
Convergence in the Padé Table For 1F1(1; c; x).
Indagationes Mathematicae (Proceedings),
Vol. 79,
Issue. 5,
p.
408.
van Rossum, H.
1979.
Padé Approximation and its Applications.
Vol. 765,
Issue. ,
p.
172.
van Rossum, H.
1981.
Padé Approximation and its Applications Amsterdam 1980.
Vol. 888,
Issue. ,
p.
341.
de Bruin, Marcel G.
1984.
Padé Approximation and its Applications Bad Honnef 1983.
Vol. 1071,
Issue. ,
p.
12.
Ando, T.
1987.
Totally positive matrices.
Linear Algebra and its Applications,
Vol. 90,
Issue. ,
p.
165.
Karlin, Samuel
1988.
I. J. Schoenberg Selected Papers.
p.
384.
Schoenberg, I. J.
1988.
I. J. Schoenberg Selected Papers.
p.
169.
Schoenberg, I. J.
1988.
I.J. Schoenberg Selected Papers.
p.
575.
Jacobsen, Lisa
and
Waadeland, Haakon
1989.
When does f(z) have a regular C-fraction expansion or a normal Padé table?.
Journal of Computational and Applied Mathematics,
Vol. 28,
Issue. ,
p.
199.
Brenti, Francesco
1991.
Log-concavity and Combinatorial Properties of Fibonacci Lattices.
European Journal of Combinatorics,
Vol. 12,
Issue. 6,
p.
459.
Wagner, David G
1992.
Total positivity of Hadamard products.
Journal of Mathematical Analysis and Applications,
Vol. 163,
Issue. 2,
p.
459.
Brenti, Francesco
1995.
Combinatorics and total positivity.
Journal of Combinatorial Theory, Series A,
Vol. 71,
Issue. 2,
p.
175.
Brenti, Francesco
1996.
Total Positivity and Its Applications.
p.
451.