Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T06:19:30.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Projections on Tree-Like banach Spaces

Published online by Cambridge University Press:  20 November 2018

A. D. Andrew
A. D. Andrew*
Affiliation:
Georgia Institute of Technology, Atlanta, Georgia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. In this paper, we investigate the ranges of projections on certain Banach spaces of functions defined on a diadic tree. The notion of a “tree-like” Banach space is due to James 4], who used it to construct the separable space JT which has nonseparable dual and yet does not contain l1. This idea has proved useful. In [3], Hagler constructed a hereditarily c0 tree space, HT, and Schechtman [6] constructed, for each 1 ≦ p ≦ ∞, a reflexive Banach space, STp with a 1-unconditional basis which does not contain lp yet is uniformly isomorphic to 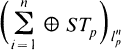for each n.

In [1] we showed that if U is a bounded linear operator on JT, then there exists a subspace W ⊂ JT, isomorphic to JT such that either U or (1 — U) acts as an isomorphism on W and UW or (1 — U)W is complemented in JT. In this paper, we establish this result for the Hagler and Schechtman tree spaces.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 5 , 01 October 1985 , pp. 908 - 920
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Andrew, A. D., The Banach space JT is primary, Pacific J. Math. 705 (1983), 9–17.Google Scholar
2. Casazza, P. G. and Lin, B. L., Projections on Banach spaces with symmetric bases, Studia Math. 52 (1974), 189–193.Google Scholar
3. Hagler, J., A counterexample to several questions about Banach spaces, Studia Math. 60 (1977), 289–308.Google Scholar
4. James, R. C., A separable somewhat reflexive Banach space with non-separable dual, Bull. A.M.S. 50 (1974), 738–743.Google Scholar
5. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I (Springer-Verlag, New York, 1977).CrossRefGoogle Scholar
6. Schechtman, G., A tree-like Tsirelson space, Pacific J. Math. 83 (1979), 523–530.Google Scholar