Article contents
Primes in Short Segments of Arithmetic Progressions
Published online by Cambridge University Press: 20 November 2018
Abstract
Consider the variance for the number of primes that are both in the interval 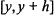 $\left[ y,\,y\,+\,h \right]$ for
$\left[ y,\,y\,+\,h \right]$ for 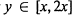 $y\,\in \,[x,\,2x]$ and in an arithmetic progression of modulus
$y\,\in \,[x,\,2x]$ and in an arithmetic progression of modulus  $q$. We study the total variance obtained by adding these variances over all the reduced residue classes modulo
$q$. We study the total variance obtained by adding these variances over all the reduced residue classes modulo  $q$. Assuming a strong form of the twin prime conjecture and the Riemann Hypothesis one can obtain an asymptotic formula for the total variance in the range when
$q$. Assuming a strong form of the twin prime conjecture and the Riemann Hypothesis one can obtain an asymptotic formula for the total variance in the range when 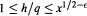 $1\le \,h/q\,\le \,{{x}^{1/2-\in }}$, for any
$1\le \,h/q\,\le \,{{x}^{1/2-\in }}$, for any 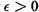 $\varepsilon \,>\,0$. We show that one can still obtain some weaker asymptotic results assuming the Generalized Riemann Hypothesis (GRH) in place of the twin prime conjecture. In their simplest form, our results are that on GRH the same asymptotic formula obtained with the twin prime conjecture is true for “almost all”
$\varepsilon \,>\,0$. We show that one can still obtain some weaker asymptotic results assuming the Generalized Riemann Hypothesis (GRH) in place of the twin prime conjecture. In their simplest form, our results are that on GRH the same asymptotic formula obtained with the twin prime conjecture is true for “almost all”  $q$ in the range
$q$ in the range 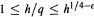 $1\le h/q\le {{h}^{1/4-\in }}$, that on averaging over
$1\le h/q\le {{h}^{1/4-\in }}$, that on averaging over  $q$ one obtains an asymptotic formula in the extended range
$q$ one obtains an asymptotic formula in the extended range 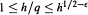 $1\le h/q\le {{h}^{1/2-\in }}$, and that there are lower bounds with the correct order of magnitude for all
$1\le h/q\le {{h}^{1/2-\in }}$, and that there are lower bounds with the correct order of magnitude for all  $q$ in the range
$q$ in the range 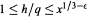 $1\le h/q\le {{x}^{1/3-\in }}$.
$1\le h/q\le {{x}^{1/3-\in }}$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 2
- Cited by


