Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T05:37:45.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Porosity and Approximate Derivatives

Published online by Cambridge University Press:  20 November 2018

A. M. Bruckner ,
M. Laczkovich ,
G. Petruska  and
B. S. Thomson
A. M. Bruckner
Affiliation:
University of California, Santa Barbara, California
M. Laczkovich
Affiliation:
Eötvös Lorand University, Budapest, Hungary
G. Petruska
Affiliation:
Simon Fraser University, Vancouver, British Columbia
B. S. Thomson
Affiliation:
Simon Fraser University, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In recent years, a considerable amount of research has been devoted to questions involving set porosity, particularly as it relates to differentiation theory. We may express the type of question in which we are interested by using the language of path derivatives and sequential derivatives. A path derivative of a function/is defined by writing

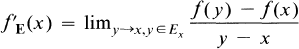
where at each point x a set Ex is given. A special case of the path derivative is the sequential derivative, defined by writing

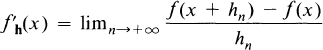
where hn is a fixed sequence of nonzero numbers converging to zero.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1149 - 1180
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Besicovitch, A. S., Diskussion der stetigen Funktionen im Zusammenhang mit der Frage über ihre Differentiierbarkeit, Bull, de l'Académie des Sciences de Russie (1925), 97–122 and 527–540.Google Scholar
2. Bruckner, A. M., Differentiation of real functions, Lect. Notes in Math. 659 (Springer-Verlag, 1978).Google Scholar
3. Bruckner, A. M. and Thomson, B. S., Porosity estimates for the Dini derivatives, Real Analysis Exchange 9 (1983-84), 508–538.Google Scholar
4. Bruckner, A. M., O'Malley, R. J. and Thomson, B. S., Path derivatives: a unified view of certain generalized derivatives, Trans. Amer. Math. Soc. 283 (1984), 97–125.Google Scholar
5. Burkill, J. C. and Haslam-Jones, U. S., The derivates and approximate derivates of measurable functions, Proc. London Math. Soc. (2) 32 (1931), 346–355.Google Scholar
6. Davies, R. O., Non-monotonic implies very oscillatory, Real Analysis Exchange 6 (1980-81), 187–191.Google Scholar
7. Dolženko, E. P., Boundary properties of arbitrary functions, Math. USSR-IZV. 1 (1967), 1–12.Google Scholar
8. Good, I. J., The approximate local monotony of measurable functions, Proc. Camb. Phil. Soc. 36 (1940), 9–13.Google Scholar
9. Jarnǐk, V., Sur les nombres derivées approximatifs, Fund. Math. 22 (1934), 4–16.Google Scholar
10. Khintchine, A., Sur la dérivation asymptotique, C. R Acad. Sci. Paris 164 (1917), 142–144.Google Scholar
11. Khintchine, A., An investigation of the structure of measurable functions, (in Russian) Mat. Sbornik 31 (1924), 265–285.Google Scholar
12. Khintchine, A., Recherches sur la structure des fonctions mesurables, Fund. Math. 9 (1927), 212–279.Google Scholar
13. Laczkovich, M. and Petruska, G, Remarks on a problem of A. M. Bruckner, Acta Math. Acad. Sci. Hungar. 38 (1981), 205–214.Google Scholar
14. O'Malley, R. J., Decomposition of approximate derivatives, Proc. Amer. Math. Soc. 69 (1978), 243–247.Google Scholar
15. Saks, S., Theory of the integral, Monografie Matematyczne 7 (Warsawa-Lwow, 1937).Google Scholar
16. Sindalovskii, G. H., Continuity and differentiability with respect to congruent sets, Soviet Math. Dokl. 1 (1961), 1217–1218.Google Scholar
17. Sindalovskii, G. H., On a generalization of derived numbers, Izv. Akad. Nauk SSSR Ser. Mat. 24 (1960), 707–720.Google Scholar
18. Sindalovskii, G. H., Continuity and differentiability with respect to congruent sets, Izv. Akad. Nauk SSSR Ser. Mat. 26 (1962), 125–142.Google Scholar
19. Sindalovskii, G. H., Congruent and asymptotic differentiability, Soviet Math. Dokl. 4 (1963), 807–809.Google Scholar
20. Sindalovskii, G. H., Differentiability with respect to congruent sets, Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965), 11–40.Google Scholar
21. Sindalovskii, G. H., On the equivalence between ordinary derivatives and the derivatives with respect to congruent sets of a certain class, Izv. Akad. Nauk SSSR Ser. Mat. 29 (1965), 987–996.Google Scholar
22. Sindalovskii, G. H., The derived numbers of continuous functions, Uspehi Mat. Nauk 21 (1966), 274–277.Google Scholar
23. Sindalovskii, G. H., The derived numbers of continuous functions, Math. USSR-Izvestia 2 (1968), 943–978.Google Scholar
24. Wos, J., [private communication, June 11, 1984].Google Scholar
25. Whitney, H., On totally differentiable and smooth functions, Pacific J. Math. 1 (1951), 143–159.Google Scholar