No CrossRef data available.
Article contents
Polynomiality of factorizations in reflection groups
Published online by Cambridge University Press: 09 December 2021
Abstract
We study the number of ways of factoring elements in the complex reflection groups
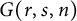 $G(r,s,n)$
as products of reflections. We prove a result that compares factorization numbers in
$G(r,s,n)$
as products of reflections. We prove a result that compares factorization numbers in
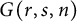 $G(r,s,n)$
to those in the symmetric group
$G(r,s,n)$
to those in the symmetric group
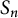 $S_n$
, and we use this comparison, along with the Ekedahl, Lando, Shapiro, and Vainshtein (ELSV) formula, to deduce a polynomial structure for factorizations in
$S_n$
, and we use this comparison, along with the Ekedahl, Lando, Shapiro, and Vainshtein (ELSV) formula, to deduce a polynomial structure for factorizations in
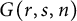 $G(r,s,n)$
.
$G(r,s,n)$
.
MSC classification
Primary:
20F55: Reflection and Coxeter groups
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society, 2021
References
Bini, G., Goulden, I. P., and Jackson, D. M., Transitive factorizations in the hyperoctahedral group. Canad. J. Math. 60(2008), no. 2, 297–312.CrossRefGoogle Scholar
Cavalieri, R. and Miles, E., Riemann surfaces and algebraic curves, London Mathematical Society Student Texts, 87, Cambridge University Press,Cambridge, 2016.CrossRefGoogle Scholar
Chapuy, G. and Stump, C., Counting factorizations of Coxeter elements into products of reflections. J. Lond. Math. Soc. (2) 90(2014), no. 3, 919–939.CrossRefGoogle Scholar
delMas, E., Hameister, T., and Reiner, V., A refined count of Coxeter element reflection factorizations. Electron. J. Combin. 25(2018), no. 1, Paper 1.28, 11.CrossRefGoogle Scholar
Douvropoulos, T., On enumerating factorizations in reflection groups. Sém. Lothar. Combin. 82(B)(2020), 12.Google Scholar
Ekedahl, T., Lando, S., Shapiro, M., and Vainshtein, A., Hurwitz numbers and intersections on moduli spaces of curves. Invent. Math. 146(2001), no. 2, 297–327.CrossRefGoogle Scholar
Goulden, I. P., Jackson, D. M., and Vainshtein, A., The number of ramified coverings of the sphere by the torus and surfaces of higher genera. Ann. Comb. 4(2000), no. 1, 27–46.CrossRefGoogle Scholar
Hurwitz, A., Ueber Riemann’sche Flächen mit gegebenen Verzweigungspunkten. Math. Ann. 39(1891), no. 1, 1–60.Google Scholar
Jackson, D. M., Some combinatorial problems associated with products of conjugacy classes of the symmetric group. J. Combin. Theory Ser. A 49(1988), no. 2, 363–369.CrossRefGoogle Scholar
Lewis, J. B. and Morales, A. H., Factorization problems in complex reflection groups. Canad. J. Math. 73(2021), no. 4, 899–946.CrossRefGoogle Scholar
Michel, J., Deligne-Lusztig theoretic derivation for Weyl groups of the number of reflection factorizations of a Coxeter element. Proc. Amer. Math. Soc. 144(2016), no. 3, 937–941.CrossRefGoogle Scholar
Shephard, G. C. and Todd, J. A., Finite unitary reflection groups. Canad. J. Math. 6(1954), 274–304.CrossRefGoogle Scholar



