Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-25T22:04:19.763Z Has data issue: false hasContentIssue false
  • English
  • Français

Poles of the Standard 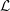${\mathcal{L}}$-function of 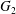$G_{2}$ and the Rallis–Schiffmann Lift

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 March 2019

Nadya Gurevich  and
Avner Segal
Nadya Gurevich
Affiliation:
School of Mathematics, Ben Gurion University of the Negev, POB 653, Be’er Sheva 84105, Israel Email: [email protected]
Avner Segal
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv 69978, Israel University of British Columbia, Vancouver BC V6T 1Z2 Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize the cuspidal representations of 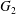$G_{2}$ whose standard 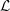${\mathcal{L}}$-function admits a pole at 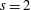$s=2$ as the image of the Rallis–Schiffmann lift for the commuting pair (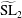$\widetilde{\text{SL}}_{2}$, 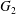$G_{2}$) in 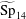$\widetilde{\text{Sp}}_{14}$. The image consists of non-tempered representations. The main tool is the recent construction, by the second author, of a family of Rankin–Selberg integrals representing the standard 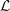${\mathcal{L}}$-function.

Keywords

automorphic representationexceptional theta-liftSiegel-Weil identity

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Secondary: 11F27: Theta series; Weil representation; theta correspondences 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 5 , October 2019 , pp. 1127 - 1161
Copyright
© Canadian Mathematical Society 2019 

Footnotes

The authors were partially supported by grants 1691/10 and 259/14 from the Israel Science Foundation.

References

Gan, Wee Teck, Multiplicity formula for cubic unipotent Arthur packets . Duke Math. J. 130(2005), no. 2, 297–320.Google Scholar
Gan, Wee Teck and Gurevich, Nadya, Nontempered A-packets of G 2: liftings from ˜SL2 . Amer. J. Math. 128(2006), no. 5, 1105–1185. https://doi.org/10.1353/ajm.2006.0040.Google Scholar
Gan, Wee Teck, Gurevich, Nadya, and Jiang, Dihua, Cubic unipotent Arthur parameters and multiplicities of square integrable automorphic forms . Invent. Math. 149(2002), no. 2, 225–265. https://doi.org/10.1007/s002220200210.Google Scholar
Gan, Wee Teck, Gross, Benedict, and Savin, Gordan, Fourier coefficients of modular forms on G 2 . Duke Math. J. 115(2002), no. 1, 105–169. https://doi.org/10.1215/S0012-7094-02-11514-2.Google Scholar
Ginzburg, David, On the standard L-function for G 2 . Duke Math. J. 69(1993), no. 2, 315–333. https://doi.org/10.1215/S0012-7094-93-06915-3.Google Scholar
Ginzburg, David and Jiang, Dihua, Periods and liftings: from G 2 to C 3 . Israel J. Math. 123(2001), 29–59. https://doi.org/10.1007/BF02784119.Google Scholar
Ginzburg, David, Rallis, Stephen, and Soudry, David, On the automorphic theta representation for simply laced groups . Israel J. Math. 100(1997), 61–116. https://doi.org/10.1007/BF02773635.Google Scholar
Ginzburg, David, Rallis, Stephen, and Soudry, David, A tower of theta correspondences for G 2 . Duke Math. J. 88(1997), no. 3, 537–624. https://doi.org/10.1215/S0012-7094-97-08821-9.Google Scholar
Gurevich, Nadya and Segal, Avner, The Rankin–Selberg integral with a non-nique model for the standard L-function of G 2 . J. Inst. Math. Jussieu 14(2015), no. 1, 149–184. https://doi.org/10.1017/S147474801300039X.Google Scholar
Helgason, Sigurdur, Groups and geometric analysis . Pure and Applied Mathematics, 113. Academic Press, Orlando, FL, 1984.Google Scholar
Hörmander, Lars, An introduction to complex analysis in several variables , Third edition., North-Holland Mathematical Library, 7. North-Holland Publishing, Amsterdam, 1990.Google Scholar
Huang, Jing-Song, Magaard, Kay, and Savin, Gordan, Unipotent representations of G 2 arising from the minimal representation of D 4 E . J. Reine Angew. Math. 500(1998), 65–81.Google Scholar
Ikeda, Tamotsu, On the location of poles of the triple L-functions . Compositio Math. 83(1992), no. 2, 187–237.Google Scholar
Ikeda, Tamotsu, On the theory of Jacobi forms and Fourier–Jacobi coefficients of Eisenstein series . J. Math. Kyoto Univ. 34(1994), no. 3, 615–636. https://doi.org/10.1215/kjm/1250518935.Google Scholar
Jiang, Dihua, G 2-periods and residual representations . J. Reine Angew. Math. 497(1998), 17–46.Google Scholar
Kudla, Stephen S., Splitting metaplectic covers of dual reductive pairs . Israel J. Math. 87(1994), 361–401. https://doi.org/10.1007/BF02773003.Google Scholar
Lapid, Erez M., A remark on Eisenstein series . In: Eisenstein series and applications . Progr. Math., 258. Birkhäuser Boston, Boston, MA, 2008, pp. 239–249.Google Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral decomposition and Eisenstein series . Cambridge Tracts in Mathematics, 113. Cambridge University Press, Cambridge, 1995.Google Scholar
Prasad, Dipendra, A brief survey on the theta correspondence . In: Number theory . Contemp. Math., 210. American Mathematical Society, Providence, RI, 1998, pp. 171–193. https://doi.org/10.1090/conm/210/02790.Google Scholar
Rallis, S. and Schiffmann, G., Theta correspondence associated to G 2 . Amer. J. Math. 111(1989), no. 5, 801–849. https://doi.org/10.2307/2374882.Google Scholar
Sahi, Siddhartha, Jordan algebras and degenerate principal series . J. Reine Angew. Math. 462(1995), 1–18. https://doi.org/10.1515/crll.1995.462.1.Google Scholar
Segal, A., The degenerate Eisenstein series attached to the Heisenberg parabolic subgroups of quasi-split forms of D 4 . Trans. Amer. Math. Soc. 370(2018), no. 8, 5983–6039. https://doi.org/10.1090/tran/7293.Google Scholar
Segal, A., The degenerate residual spectrum of quasi-split forms of Spin 8 associated to the Heisenberg parabolic subgroup. 2018. arxiv:1804.08849.Google Scholar
Segal, A., Rankin-Selberg integrals with a non-unique model for the standard L-function of cuspidal representations of the exceptional group of type G 2. Ph.D. thesis, Ben-Gurion University of the Negev, 2016.Google Scholar
Segal, A., A family of new-way integrls for the standard L-function of cuspidal representations of the exceptional group of type G 2 . Int. Math. Res. Not. IMRN (2017), no. 7, 2014–2099. https://doi.org/10.1093/imrn/rnw090.Google Scholar
Shahidi, Freydoon, Whittaker models for real groups . Duke Math. J. 47(1980), no. 1, 99–125. https://doi.org/10.1215/S0012-7094-80-04708-0.Google Scholar
Steinberg, Robert, Lectures on Chevalley groups . Yale University, New Haven, Conn., 1968.Google Scholar
Waldspurger, J.-L., Correspondance de Shimura . J. Math. Pures Appl. 59(1980), no. 1, 1–132.Google Scholar
Waldspurger, J.-L., Correspondances de Shimura et quaternions . Forum Math. 3(1991), no. 3, 219–307.Google Scholar
Weissman, Martin H., The Fourier-Jacobi map and small representations . Represent. Theory 7(2003), 275–299. https://doi.org/10.1090/S1088-4165-03-00197-3.Google Scholar
Winarsky, Norman, Reducibility of principal series representations of p-adic Chevalley groups . Amer. J. Math. 100(1978), no. 5, 941–956. https://doi.org/10.2307/2373955.Google Scholar