Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Akcoglu, M. A.
and
Sucheston, L.
1975.
Weak convergence of positive contractions implies strong convergence of averages.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 32,
Issue. 1-2,
p.
139.
Akcoglu, M. A.
and
Sucheston, L.
1975.
On weak and strong convergence of positive contractions in 𝐿_{𝑝} spaces.
Bulletin of the American Mathematical Society,
Vol. 81,
Issue. 1,
p.
105.
Akcoglu, M. A.
and
Sucheston, L.
1975.
Remarks on dilations in 𝐿_{𝑝}-spaces.
Proceedings of the American Mathematical Society,
Vol. 53,
Issue. 1,
p.
80.
McGrath, S. A.
1976.
An abelian ergodic theorem for semigroups in 𝐿_{𝑝} space.
Proceedings of the American Mathematical Society,
Vol. 54,
Issue. 1,
p.
231.
Duncan, Richard
1977.
Some Pointwise Convergence Results in Lp(μ), 1 < p < ∞.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 3,
p.
277.
De La Torre, A.
1977.
A Dominated Ergodic Theorem for Contractions with Fixed Points.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 1,
p.
89.
Kern, Martin
Nagel, Rainer
and
Palm, G�nther
1977.
Dilations of positive operators: Construction and ergodic theory.
Mathematische Zeitschrift,
Vol. 156,
Issue. 3,
p.
265.
Akcoglu, M. A.
and
Sucheston, L.
1977.
Dilations of Positive Contractions on Lp Spaces*.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 3,
p.
285.
Akcoglu, Mustafa A.
and
Kopp, P. Ekkehard
1977.
Construction of dilations of positiveL p -contractions.
Mathematische Zeitschrift,
Vol. 155,
Issue. 2,
p.
119.
Coifman, R. R.
Rochberg, R.
and
Weiss, Guido
1978.
Linear Spaces and Approximation / Lineare Räume und Approximation.
p.
53.
1978.
Measure and Integral.
p.
549.
Peller, V. V.
1978.
Approximations by isometries and V. I. Matsaev's hypothesis for absolute contractions of the space Lp.
Functional Analysis and Its Applications,
Vol. 12,
Issue. 1,
p.
29.
Akcoglu, Mustafa A.
1979.
Ergodic Theory.
Vol. 729,
Issue. ,
p.
13.
Olsen, James H.
1980.
The Individual Ergodic Theorem for Contractions with Fixed Points.
Canadian Mathematical Bulletin,
Vol. 23,
Issue. 1,
p.
115.
Millet, Annie
1980.
Sur le th�or�me en moyenne d'Akcoglu-Sucheston.
Mathematische Zeitschrift,
Vol. 172,
Issue. 3,
p.
213.
Yoshimoto, T.
1980.
Some inequalities for ergodic power functions.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 36,
Issue. 1-2,
p.
19.
Sato, Ryotaro
1981.
An Extrapolation Theorem for Contractions with Fixed Points.
Canadian Mathematical Bulletin,
Vol. 24,
Issue. 2,
p.
199.
Derriennic, Y.
and
Krengel, U.
1981.
Subadditive mean ergodic theorems.
Ergodic Theory and Dynamical Systems,
Vol. 1,
Issue. 1,
p.
33.
Nagel, Rainer
and
Palm, Günther
1982.
Lattice Dilations of Positive Contractions on Lp-Spaces.
Canadian Mathematical Bulletin,
Vol. 25,
Issue. 3,
p.
371.
Olsen, James H.
1983.
A Multiple Sequence Ergodic Theorem.
Canadian Mathematical Bulletin,
Vol. 26,
Issue. 4,
p.
493.


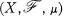 be a measure space and
be a measure space and 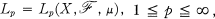 the usual Banach spaces. A linear operator
the usual Banach spaces. A linear operator