Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T07:36:19.038Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbation of the Continuous Spectrum of Systems of Ordinary Differential Operators

Published online by Cambridge University Press:  20 November 2018

John B. Butler Jr.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

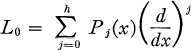
be an ordinary differential operator of order h whose coefficients are (η, η) matrices defined on the interval 0 ≤ x < ∞, hη = n = 2v. Let the operator L0 be formally self adjoint and let v boundary conditions be given at x = 0 such that the eigenvalue problem

(1.1)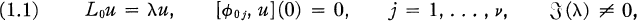

has no non-trivial square integrable solution. This paper deals with the perturbed operator L∈ = L0 + ∈q where ∈ is a real parameter and q(x) is a bounded positive (η, η) matrix operator with piecewise continuous elements 0 ≤ x < ∞. Sufficient conditions involving L0, q are given such that L∈ determines a selfadjoint operator H∈ and such that the spectral measure E∈(Δ′) corresponding to H∈ is an analytic function of ∈, where Δ′ is a subset of a fixed bounded interval Δ = [α, β]. The results include and improve results obtained for scalar differential operators in an earlier paper (3).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 359 - 378
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Agudo, F. R. D. and Wolf, F., Propriétés spectrales des équations différentielles non-autoadjoint, Rend. Acad. Naz. dei Lincei, Scienz fisiche etc. ser. 8, 24, fasc. 6 (1958), 643–645.Google Scholar
2. Brownell, F. H., Perturbation of the n-dimensional Schrôdinger differential operator, Abstract no. 430t, Bull. Amer. Math. Soc, 60 (1954), 346.Google Scholar
3. Butler, J. B., Perturbation of the continuous spectrum of even order differential operators, Can. J. Math., 12 (1960), 309–323.Google Scholar
4. Coulson, C. A., Waves (Edinburgh, 1941).Google Scholar
5. Friedrichs, K. O., Symmetric hyperbolic linear differential equations, Comm. Pure Appl. Math., 7 (1954), 345–392.Google Scholar
6. Heinz, E.., Halbbeschrânktheit gewohnlicher Differentialoperatoren hôherer Ordnung, Math. Ann., 135 (1958), 1–49.Google Scholar
7. Kodaira, K., On the differential equations of any even order and the corresponding eigenfunction expansions, Amer. J. Math., 72 (1950), 502–543.Google Scholar
8. Kuroda, S. T., Perturbation of the continuous spectra by unbounded operators, J. Math. Soc. Japan, 11 (1959), 247–262.Google Scholar
9. Mathews, P. M., Vibration of a beam on an elastic foundation, Z. Angev. Math. Mech., 38 (1958), 105–115.Google Scholar
10. Moser, J., Stôrungstheorie des kontinuierlichen Spectrums, Math. Ann., 125 (1953), 366–393.Google Scholar
11. Nagy, B. Sz. and Riesz, F., Leçons d'analyse fonctionnelle, Hungarian Acad. Sci. (Budapest, 1953).Google Scholar
12. Stone, M. H., Linear transformations in Hilbert space, Amer. Math. Soc. Coll. Pub., 15 (1932).Google Scholar
13. Titchmarsh, E. C., Eigenfunction Expansions, Part 2, (London, 1958).Google Scholar
14. Windau, W., Ueber lineare Differentialgleichungen vierter Ordnung mit Singularitäten und die dazugehbrigen Darstellungen willkürlicher Functionen, Math. Ann., 83 (1921), 256–279.Google Scholar