Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-02T23:45:23.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Partially Bounded Solutions of Linear Ordinary Differential Equations

Published online by Cambridge University Press:  20 November 2018

David Lowell Lovelady
David Lowell Lovelady*
Affiliation:
Florida State University, Tallahassee, Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R, R+, and R- be the intervals (-∞, ∞), [0, ∞), and ( — ∞, 0] respectively. Let m be a positive integer, and let 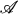be the algebra of all m X m matrices. Let A be a locally integrable function from R to We propose to study the problems

(NH) u‘(t) = f(t) + A﹛t)u﹛t)

and

(H) v‘(t) =A(t)v(t)

in Rm. (H) and (NH) will denote whole-line problems, whereas (H)+, (NH)+, (H)-, and (NH)- will denote corresponding semi-axis problems.

In [1] (see also [2, Theorem 1, p. 131]), W. A. Coppel obtained necessary and sufficient conditions for each bounded Continuous/ on R+ to yield at least one bounded solution u of (NH)+. The present author [3] has determined that an analogous result holds for (NH).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 2 , 01 April 1975 , pp. 366 - 371
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Coppel, W. A., On the stability of ordinary differential equations, J. London Math. Soc. 38 (1963), 255–260.Google Scholar
2. Coppel, W. A., Stability and asymptotic behavior of differential equations (D. C. Heath & Co., Boston, 1965).Google Scholar
3. Lovelady, D. L., Bounded solutions of whole-line differential equations, Bull. Amer. Math. Soc. 79 (1973), 752–753.Google Scholar
4. Lovelady, D. L., Boundedness and ordinary differential equations on the real line, J. London Math. Soc. 7 (1973), 597–603.Google Scholar
5. Lovelady, D. L., Relative boundedness and second order differential equations, Tôhoku Math. J. 25 (1973), 365–374.Google Scholar
6. Schechter, M., Principles of functional analysis (Academic Press, New York, 1971).Google Scholar