Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T17:20:08.635Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial Hasse Invariants, Partial Degrees, and the Canonical Subgroup

Published online by Cambridge University Press:  20 November 2018

Stephane Bijakowski
Stephane Bijakowski*
Affiliation:
Imperial College, Department of Mathematics, 180 Queen's Gate, London SW7 2AZ UK email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If the Hasse invariant of a 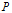$P$ -divisible group is small enough, then one can construct a canonical subgroup inside its 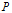$P$-torsion. We prove that, assuming the existence of a subgroup of adequate height in the 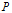$P$-torsion with high degree, the expected properties of the canonical subgroup can be easily proved, especially the relation between its degree and the Hasse invariant. When one considers a 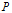$P$-divisible group with an action of the ring of integers of a (possibly ramified) finite extension of 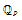${{\mathbb{Q}}_{P}}$ , then much more can be said. We define partial Hasse invariants (which are natural in the unramified case, and generalize a construction of Reduzzi and Xiao in the general case), as well as partial degrees. After studying these functions, we compute the partial degrees of the canonical subgroup.

Keywords

11F8511F4611S15canonical subgroupHasse invariantp-divisible group
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 4 , 01 August 2018 , pp. 742 - 772
Copyright
Copyright © Canadian Mathematical Society 2018

References

[A-M] Abbes, A. et Mokrane, A., Sous-groupes canoniques et cycles évanescents p-adiques pour les variétés abéliennes. Publ. Math. Inst. Hautes Études Sci. 99(2004), 117–162. http://dx.doi.Org/10.1007/s10240-004-0022-x Google Scholar
[A-Ga] Andreatta, E. and Gasbarri, C., The canonical subgroup for families of abelian varieties. Compos. Math. 143(2007), no. 3, 566–602. http://dx.doi.Org/10.1112/S0010437X07002813 Google Scholar
[A-Go] Andreatta, E. and Goren, E., Geometry of Hilbert modular varieties over totally ramified primes. Inter. Math. Res. Not. 33(2003), 1785–1835. http://dx.doi.Org/10.1155/S1073792803204037 Google Scholar
[BBM] Berthelot, P., Breen, L., and Messing, W., Théorie de Dieudonné cristalline II. Lectures Notes in Mathematics, 930, Springer-Verlag, Berlin, 1982. http://dx.doi.Org/10.1007/BFb0093025 Google Scholar
[Bi] Bijakowski, S., Formes modulaires surconvergentes, ramification et classicité. Ann. Inst. Fourier, to appear.Google Scholar
[Bo] Bosch, S., Lectures on formal and rigid geometry. Lecture Notes in Mathematics, 2105, Springer, Cham, 2014. http://dx.doi.org/10.1007/978-3-319-04417-0 Google Scholar
[Co] Conrad, B., Higher-level canonical subgroups in abelian varieties, Preprint, 2005. http://math.stanford.edu/∼conrad/ Google Scholar
[Fa] Fargues, L., La filtration de Harder-Narasimhan des schémas en groupes finis et plats. J. Reine Angew. Math. 645(2010), 1–39. http://dx.doi.org/10.1515/crelle.2010.058 Google Scholar
[Fa2] Fargues, L., La filtration canonique des points de torsion des groupes p-divisibles. (French) Ann. Sci. de l'Éc. Norm. Supér. 44(2011), 905–961.Google Scholar
[G-K] Goren, E. and Kassaei, P., Canonical subgroups over Hilbert modular varieties. J. Reine Angew. Math. 670(2012), 1–63. http://dx.doi.Org/10.1515/CRELLE.2011.149 Google Scholar
[Ha] Hattori, S., Canonical subgroups via Breuil-Kisin modules. Math. Z. 274(2013), 933–953. http://dx.doi.Org/10.1007/s00209-012-1102-0 Google Scholar
[Kas] Kassaei, P., A gluing lemma and overconvergent modular forms. Duke Math. J. 132(2006), 509–529. http://dx.doi.org/10.1215/S0012-7094-06-13234-9 Google Scholar
[Kat] Katz, N., p-adic properties of modular schemes and modular forms. In: Modular functions of one variable, III, Lecture Notes in Mathematics, 350, Springer, Berlin, 1973, pp. 69–190.Google Scholar
[Lu] Lubin, J., Canonical subgroups of formal groups. Trans. Amer. Math. Soc. 251(1979), 103–127. http://dx.doi.org/10.1090/S0002-9947-1979-0531971-4 Google Scholar
[P-R] Pappas, G. and Rapoport, M., Local models in the ramified case II. Splitting models. Duke Math. J. 127(2005), 193–250. http://dx.doi.org/10.1215/S0012-7094-04-12721-6 Google Scholar
[Ra] Raynaud, M., Schémas en groupes de type (p,p,…,p). Bull. Soc. Math. France 102(1974), 241–280.Google Scholar
[R-X] Reduzzi, D. and Xiao, L., Partial Hasse invariants on splitting models of Hilbert modular varieties. To appear, Annales Scientifiques de TENS, 2014.Google Scholar
[Sa] Sasaki, S., Integral models of Hilbert modular varieties in the ramified case, deformations of modular Galois representations, and weight one forms, Preprint, 2014. http://www.cantabgold.net/users/s.sasaki.03/ Google Scholar
[Sch] Scholze, P., On torsion in the cohomology of locally symmetric varieties. Ann. of Math. 182(2015), no. 3, 945–1066. http://dx.doi.org/10.4007/annals.2015.182.33 Google Scholar
[T-O] Tate, J. and Oort, F., Group schemes of prime order. Ann. Sci. École Norm. Sup. (4) 3(1970), 1–21.Google Scholar
[Ti] Tian, Y., Canonical subgroups ofBarsotti-Tate groups. Ann. of Math. 172(2010), 955–988. http://dx.doi.org/10.4007/annals.2010.172.955 Google Scholar