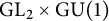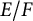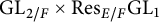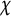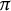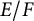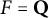1 Introduction
This paper is a case study in the construction of p-adic L-functions by the “soft” method of glueing ratios of matching families of global and local zeta integrals. The local integrals are constructed and then inserted into the global context by using the local Langlands correspondence in families (see [Reference DisegniDis20] and the references therein). The method, whose deployment seems new for non-abelian families, should be of wide applicability; we give a brief introductory description in Section 1.2.
The specific context and arithmetic interest of our work is the following. Let F be a totally real field, let
![]() $E/F$
be a totally imaginary quadratic extension, and let p be a rational prime. We construct a meromorphic function
$E/F$
be a totally imaginary quadratic extension, and let p be a rational prime. We construct a meromorphic function
![]() $\mathscr {L}_{p}(\mathscr {V})$
on Hida families for
$\mathscr {L}_{p}(\mathscr {V})$
on Hida families for
![]() $\mathrm {GL}_{2/F}\times \mathrm {Res}_{E/F}\mathrm {GL}_{1}$
that interpolates critical values
$\mathrm {GL}_{2/F}\times \mathrm {Res}_{E/F}\mathrm {GL}_{1}$
that interpolates critical values
 $$ \begin{align*}{L(1/2, \pi_{E}\otimes\chi)\over L(1, \pi, \mathrm{ad})},\end{align*} $$
$$ \begin{align*}{L(1/2, \pi_{E}\otimes\chi)\over L(1, \pi, \mathrm{ad})},\end{align*} $$
for p-ordinary automorphic representations
![]() $\pi \boxtimes \chi $
such that
$\pi \boxtimes \chi $
such that
![]() $\chi $
has lower weights than
$\chi $
has lower weights than
![]() $\pi $
. (The precise statement is Theorem A; note that in our normalization, the above numerators are not necessarily central values.) The function
$\pi $
. (The precise statement is Theorem A; note that in our normalization, the above numerators are not necessarily central values.) The function
![]() $\mathscr {L}_{p}(\mathscr {V})$
is new (if not surprising) at least when
$\mathscr {L}_{p}(\mathscr {V})$
is new (if not surprising) at least when
![]() $E/F$
does not split above p; for a discussion of previous related works, see Section 1.1.6.
$E/F$
does not split above p; for a discussion of previous related works, see Section 1.1.6.
The interpolation property of
![]() $\mathscr {L}_{p}(\mathscr {V})$
holds at all classical points satisfying the weight condition and lying outside the polar locus (on which we have partial control), and it provides an entirely explicit and complete characterization of the function, in the spirit of [Reference HidaHid96]. Its generality and precision are key to some arithmetic applications in [Reference DisegniDis/b], which motivated our choice of case. In that paper, we prove, first, the p-adic Beilinson–Bloch–Kato conjecture in analytic rank
$\mathscr {L}_{p}(\mathscr {V})$
holds at all classical points satisfying the weight condition and lying outside the polar locus (on which we have partial control), and it provides an entirely explicit and complete characterization of the function, in the spirit of [Reference HidaHid96]. Its generality and precision are key to some arithmetic applications in [Reference DisegniDis/b], which motivated our choice of case. In that paper, we prove, first, the p-adic Beilinson–Bloch–Kato conjecture in analytic rank
![]() $1$
for (conjugate-)self-dual motives attached to representations
$1$
for (conjugate-)self-dual motives attached to representations
![]() $\pi _{E}\otimes \chi $
as above; and second, one divisibility in an Iwasawa Main Conjecture for the cyclotomic derivative
$\pi _{E}\otimes \chi $
as above; and second, one divisibility in an Iwasawa Main Conjecture for the cyclotomic derivative
![]() $\mathrm {d}^{\sharp }\mathscr {L}_{p}(\mathscr {V})$
of
$\mathrm {d}^{\sharp }\mathscr {L}_{p}(\mathscr {V})$
of
![]() $\mathscr {L}_{p}(\mathscr {V})$
along a self-dual locus. Both results, new or partly new even when
$\mathscr {L}_{p}(\mathscr {V})$
along a self-dual locus. Both results, new or partly new even when
![]() $F=\mathbf {Q}$
and
$F=\mathbf {Q}$
and
![]() $E/F$
splits at p, rely on a p-adic Gross–Zagier formula for
$E/F$
splits at p, rely on a p-adic Gross–Zagier formula for
![]() $\mathrm {d}^{\sharp }\mathscr {L}_{p}(\mathscr {V})$
. In turn, that formula is proved by analytically continuing formulas from [Reference DisegniDis17, Reference DisegniDisa] for the central derivatives of certain cyclotomic p-adic L-functions
$\mathrm {d}^{\sharp }\mathscr {L}_{p}(\mathscr {V})$
. In turn, that formula is proved by analytically continuing formulas from [Reference DisegniDis17, Reference DisegniDisa] for the central derivatives of certain cyclotomic p-adic L-functions
![]() $\mathscr {L}_{p}(V_{(\pi , \chi )}, s)$
attached to those representations
$\mathscr {L}_{p}(V_{(\pi , \chi )}, s)$
attached to those representations
![]() $\pi \boxtimes \chi $
as above that have minimal weights. The continuation argument thus requires to exactly identify the collection
$\pi \boxtimes \chi $
as above that have minimal weights. The continuation argument thus requires to exactly identify the collection
![]() $\{(\mathscr {L}_{p}(V_{(\pi , \chi )} , s)_{(\pi ,\chi )}\}$
of single-variable functions as a set of specializations of a multivariable analytic function, which is indeed our
$\{(\mathscr {L}_{p}(V_{(\pi , \chi )} , s)_{(\pi ,\chi )}\}$
of single-variable functions as a set of specializations of a multivariable analytic function, which is indeed our
![]() $\mathscr {L}_{p}(\mathscr {V})$
.
$\mathscr {L}_{p}(\mathscr {V})$
.
It would be interesting to extend our results to the nonordinary case by the method of [Reference Andreatta and IovitaAI21, Reference UrbanUrb14]. As for further arithmetic directions in the ordinary case,Footnote
1
the main remaining goal is perhaps the full Iwasawa Main Conjecture for
![]() $\mathscr {L}_{p}(\mathscr {V})$
. This was proved by Skinner and Urban [Reference Skinner and UrbanSU14] and Wan [Reference WanWan15] in the split case; in the nonsplit case, results toward it (when
$\mathscr {L}_{p}(\mathscr {V})$
. This was proved by Skinner and Urban [Reference Skinner and UrbanSU14] and Wan [Reference WanWan15] in the split case; in the nonsplit case, results toward it (when
![]() $F=\mathbf {Q}$
) were recently obtained by Büyükboduk and Lei [Reference Büyükboduk and LeiBL]. A second goal is the remaining divisibility in the Main Conjecture for the cyclotomic derivative of
$F=\mathbf {Q}$
) were recently obtained by Büyükboduk and Lei [Reference Büyükboduk and LeiBL]. A second goal is the remaining divisibility in the Main Conjecture for the cyclotomic derivative of
![]() $\mathscr {L}_{p}(\mathscr {V})$
(cf. [Reference DisegniDis/b, Theorem E]); in view of the p-adic Gross–Zagier formula of [Reference DisegniDis/b], this is equivalent to a suitable generalization of Perrin-Riou’s main conjecture for Heegner points, which in its original form was recently proved by Burungale, Castella, and Kim [Reference Burungale, Castella and KimBCK21].
$\mathscr {L}_{p}(\mathscr {V})$
(cf. [Reference DisegniDis/b, Theorem E]); in view of the p-adic Gross–Zagier formula of [Reference DisegniDis/b], this is equivalent to a suitable generalization of Perrin-Riou’s main conjecture for Heegner points, which in its original form was recently proved by Burungale, Castella, and Kim [Reference Burungale, Castella and KimBCK21].
1.1 Statement of the main result
We move toward stating our main theorem, leaving a few of the detailed definitions of the objects involved to the body of the paper.
1.1.1 p-adic automorphic representations
Consider the algebraic groups over F
If
![]() $v_{0} $
is a place of
$v_{0} $
is a place of
![]() $\mathbf {Q}$
, we denote
$\mathbf {Q}$
, we denote
A (numerical)
![]() $v_{0}$
-adic weight for
$v_{0}$
-adic weight for
![]() $\mathrm {G}$
is a tuple
$\mathrm {G}$
is a tuple
![]() $\underline {w}:= (w_{0}, w= (w_{\tau })_{\tau \in \Sigma _{v_{0}}})$
of integers, all of the same parity, such that
$\underline {w}:= (w_{0}, w= (w_{\tau })_{\tau \in \Sigma _{v_{0}}})$
of integers, all of the same parity, such that
![]() $w_{\tau }\geq 0$
for all
$w_{\tau }\geq 0$
for all
![]() $\tau $
. It is said cohomological if
$\tau $
. It is said cohomological if
![]() $w_{\tau }\geq 2$
for all
$w_{\tau }\geq 2$
for all
![]() $\tau $
. A weight for
$\tau $
. A weight for
![]() $\mathrm {H}$
is a tuple
$\mathrm {H}$
is a tuple
![]() $\underline {l}=(l_{0},l=( l_{\tau })_{\tau \in \Sigma _{v_{0}}})$
of integers of the same parity. Finally, if
$\underline {l}=(l_{0},l=( l_{\tau })_{\tau \in \Sigma _{v_{0}}})$
of integers of the same parity. Finally, if
![]() $\underline {w}$
and
$\underline {w}$
and
![]() $\underline {l}$
are weights for
$\underline {l}$
are weights for
![]() $\mathrm {G}$
and
$\mathrm {G}$
and
![]() $\mathrm {H}$
, the associated contracted weight for
$\mathrm {H}$
, the associated contracted weight for
![]() $\mathrm {G}\times \mathrm {H}$
isFootnote
2
$\mathrm {G}\times \mathrm {H}$
isFootnote
2
If
![]() $\underline {w}$
is a p-adic weight (say, for
$\underline {w}$
is a p-adic weight (say, for
![]() $\mathrm {G}$
) and
$\mathrm {G}$
) and
![]() $\iota \colon \overline {\mathbf {Q}}_{p}\hookrightarrow \mathbf {C}$
is an embedding, we denote
$\iota \colon \overline {\mathbf {Q}}_{p}\hookrightarrow \mathbf {C}$
is an embedding, we denote
![]() $\underline {w}^{\iota }:= (w_{0}, (w_{\tau })_{\iota \circ \tau \colon F\hookrightarrow \mathbf {C}})$
. (In fact,
$\underline {w}^{\iota }:= (w_{0}, (w_{\tau })_{\iota \circ \tau \colon F\hookrightarrow \mathbf {C}})$
. (In fact,
![]() $\underline {w}^{\iota }$
only depends on
$\underline {w}^{\iota }$
only depends on
![]() $\iota _{|L}$
if
$\iota _{|L}$
if
![]() $\underline {w}$
is rational over the finite extension L of
$\underline {w}$
is rational over the finite extension L of
![]() $\mathbf {Q}_{p}$
in the sense that
$\mathbf {Q}_{p}$
in the sense that
![]() $\mathrm {Gal}(\overline {\mathbf {Q}}_{p}/L)$
fixes
$\mathrm {Gal}(\overline {\mathbf {Q}}_{p}/L)$
fixes
![]() $\underline {w}$
.) Let
$\underline {w}$
.) Let
![]() $\mathbf {A}$
be the ring of adèles of F. An automorphic representation of archimedean weight
$\mathbf {A}$
be the ring of adèles of F. An automorphic representation of archimedean weight
![]() $\underline {w}$
is a complex automorphic representation
$\underline {w}$
is a complex automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {G}(\mathbf {A})$
such that
$\mathrm {G}(\mathbf {A})$
such that
![]() $\pi _{\infty }=\pi _{\underline {w}}:=\otimes _{\tau \colon F\hookrightarrow \mathbf {R}} \pi _{(w_{0}, w_{\tau })}$
, where
$\pi _{\infty }=\pi _{\underline {w}}:=\otimes _{\tau \colon F\hookrightarrow \mathbf {R}} \pi _{(w_{0}, w_{\tau })}$
, where
![]() $\pi _{(w_{0}, w_{\tau })}$
is the discrete series of
$\pi _{(w_{0}, w_{\tau })}$
is the discrete series of
![]() $\mathrm {GL}_{2}(F_{\tau })$
of weight
$\mathrm {GL}_{2}(F_{\tau })$
of weight
![]() $w_{\tau }$
and central character
$w_{\tau }$
and central character
![]() $z\mapsto z^{w_{0}}$
. If L is p-adic, we define an automorphic representation of
$z\mapsto z^{w_{0}}$
. If L is p-adic, we define an automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
of weight
$\mathrm {G}(\mathbf {A})$
of weight
![]() $\underline {w}$
over L to be a representation
$\underline {w}$
over L to be a representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {G}(\mathbf {A}^{\infty })$
on an L-vector space, such that for every
$\mathrm {G}(\mathbf {A}^{\infty })$
on an L-vector space, such that for every
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, the representation
$\iota \colon L\hookrightarrow \mathbf {C}$
, the representation
of
![]() $\mathrm {G}(\mathbf {A})$
is automorphic.Footnote
3
$\mathrm {G}(\mathbf {A})$
is automorphic.Footnote
3
To the representation
![]() $\pi $
over L is attached a two-dimensional representation
$\pi $
over L is attached a two-dimensional representation
![]() $V_{\pi }$
of
$V_{\pi }$
of
![]() $G_{F}:=\mathrm {Gal}(\overline {F}/F)$
; denoting by
$G_{F}:=\mathrm {Gal}(\overline {F}/F)$
; denoting by
![]() $V_{\pi ,v}$
its restriction to a decomposition group at a place v of F, the representation
$V_{\pi ,v}$
its restriction to a decomposition group at a place v of F, the representation
![]() $V_{\pi }$
is characterized by
$V_{\pi }$
is characterized by
![]() $L(V_{\pi ,v},s)=L(s+1/2, \pi _{v})$
for all v (this is the “Hecke” normalization of the Langlands correspondence, cf. [Reference DeligneDel73, Section 3.2]). We say that
$L(V_{\pi ,v},s)=L(s+1/2, \pi _{v})$
for all v (this is the “Hecke” normalization of the Langlands correspondence, cf. [Reference DeligneDel73, Section 3.2]). We say that
![]() $\pi $
is ordinary
Footnote
4
if, for each place
$\pi $
is ordinary
Footnote
4
if, for each place
![]() $v\vert p$
of F, there is a nontrivial
$v\vert p$
of F, there is a nontrivial
![]() $G_{F_{v}}$
-stable filtration
$G_{F_{v}}$
-stable filtration
such that the character
![]() $\alpha _{\pi , v}^{\circ }\colon F_{v}^{\times }\to L^{\times }$
corresponding to
$\alpha _{\pi , v}^{\circ }\colon F_{v}^{\times }\to L^{\times }$
corresponding to
![]() $V^{+}_{\pi , v}(-1)$
has values in
$V^{+}_{\pi , v}(-1)$
has values in
![]() $\mathscr {O}_{L}^{\times }$
.
$\mathscr {O}_{L}^{\times }$
.
Let L be a p-adic field splitting E, suppose chosen for each
![]() $\tau \colon F\hookrightarrow L$
an extension
$\tau \colon F\hookrightarrow L$
an extension
![]() $\tau '$
to E,Footnote
5
and let
$\tau '$
to E,Footnote
5
and let
![]() $\tau ^{\prime {c}}=\tau '\circ c$
for the complex conjugation c of
$\tau ^{\prime {c}}=\tau '\circ c$
for the complex conjugation c of
![]() $E/F$
. A Hecke character of
$E/F$
. A Hecke character of
![]() $\mathrm {H}$
of weight
$\mathrm {H}$
of weight
![]() $\underline {l} $
over the p-adic field L is a locally algebraic character
$\underline {l} $
over the p-adic field L is a locally algebraic character
![]() $\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\infty , \times }\to L^{\times }$
such that
$\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\infty , \times }\to L^{\times }$
such that
for all
![]() $t_{p}$
in some neighborhood of
$t_{p}$
in some neighborhood of
![]() $1\in E_{p}^{\times }$
. We let
$1\in E_{p}^{\times }$
. We let
![]() $V_{\chi }$
be the one-dimensional
$V_{\chi }$
be the one-dimensional
![]() $G_{E}$
-representation corresponding to
$G_{E}$
-representation corresponding to
![]() $\chi $
.
$\chi $
.
1.1.2 L-values
Let
![]() $\pi $
(respectively,
$\pi $
(respectively,
![]() $\chi $
) be a complex automorphic representation of
$\chi $
) be a complex automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
(respectively,
$\mathrm {G}(\mathbf {A})$
(respectively,
![]() $\mathrm {H}(\mathbf {A})$
), and let
$\mathrm {H}(\mathbf {A})$
), and let
![]() $\pi _{E}$
denote the base change of
$\pi _{E}$
denote the base change of
![]() $\pi $
to E. Let us also introduce the convenient notation
$\pi $
to E. Let us also introduce the convenient notation
(to be thought of as referring to a “virtual motive”).
Let
![]() $\eta \colon F^{\times }\backslash \mathbf {A}^{\times } \to \{\pm 1\}$
be the character associated with
$\eta \colon F^{\times }\backslash \mathbf {A}^{\times } \to \{\pm 1\}$
be the character associated with
![]() $E/F$
, and let
$E/F$
, and let
 $$ \begin{align*}\begin{aligned} \mathscr{L}(V_{(\pi, \chi), v},0)&:= {\zeta_{F,v}(2) L(1/2,\pi_{E, v}\otimes\chi_{v}) \over {L(1, \eta_{v})L( 1, \pi_{v}, \mathrm{ad})}} \cdot \begin{cases} 1, \quad &\text{if}\ v\nmid\infty \\ \pi^{-1}, &\text{if}\ v\vert \infty\end{cases} \quad \in \mathbf{C},\\ \mathscr{L}(V_{(\pi, \chi)},0)&:= \prod_{v} \mathscr{L}(V_{(\pi, \chi), v},0), \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \mathscr{L}(V_{(\pi, \chi), v},0)&:= {\zeta_{F,v}(2) L(1/2,\pi_{E, v}\otimes\chi_{v}) \over {L(1, \eta_{v})L( 1, \pi_{v}, \mathrm{ad})}} \cdot \begin{cases} 1, \quad &\text{if}\ v\nmid\infty \\ \pi^{-1}, &\text{if}\ v\vert \infty\end{cases} \quad \in \mathbf{C},\\ \mathscr{L}(V_{(\pi, \chi)},0)&:= \prod_{v} \mathscr{L}(V_{(\pi, \chi), v},0), \end{aligned}\end{align*} $$
where the product (in the sense of analytic continuation) is over all places. These are the L-values we will interpolate.
1.1.3 Interpolation factors
Let L be a finite extension of
![]() $\mathbf {Q}_{p}$
, let
$\mathbf {Q}_{p}$
, let
![]() $\pi $
be an ordinary automorphic representation of
$\pi $
be an ordinary automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
over L, with a locally algebraic central character
$\mathrm {G}(\mathbf {A})$
over L, with a locally algebraic central character
![]() $\omega _{\pi }\colon \mathbf {A}^{\infty , \times }\to L^{\times }$
, let
$\omega _{\pi }\colon \mathbf {A}^{\infty , \times }\to L^{\times }$
, let
![]() $\chi \colon \mathrm {H}(F)\backslash \mathrm {H}(\mathbf {A})\to L^{\times }$
be a locally algebraic character, and set
$\chi \colon \mathrm {H}(F)\backslash \mathrm {H}(\mathbf {A})\to L^{\times }$
be a locally algebraic character, and set
![]() $\omega _{\chi }:= \chi _{|\mathbf {A}^{\infty , \times }}$
. Let
$\omega _{\chi }:= \chi _{|\mathbf {A}^{\infty , \times }}$
. Let
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
be an embedding, and let
$\iota \colon L\hookrightarrow \mathbf {C}$
be an embedding, and let
![]() $\psi =\prod _{v}\psi _{v}\colon F\backslash \mathbf {A}\to \mathbf {C}^{\times }$
be the standard additive character such that
$\psi =\prod _{v}\psi _{v}\colon F\backslash \mathbf {A}\to \mathbf {C}^{\times }$
be the standard additive character such that
![]() $\psi _{\infty }(x)=e^{2\pi i \mathrm {Tr}_{F_{\infty }/\mathbf {R}}(x)}$
.
$\psi _{\infty }(x)=e^{2\pi i \mathrm {Tr}_{F_{\infty }/\mathbf {R}}(x)}$
.
If
![]() $v\vert p$
, let
$v\vert p$
, let
![]() $\mathrm {ad} (V_{\pi ,v})(1)^{++}:= \mathrm {Hom}\,(V_{\pi ,v}^{-}, V_{\pi , v}^{+})$
, and define
$\mathrm {ad} (V_{\pi ,v})(1)^{++}:= \mathrm {Hom}\,(V_{\pi ,v}^{-}, V_{\pi , v}^{+})$
, and define
 $$ \begin{align}\begin{aligned} \qquad e_{v}(V_{(\pi^{\iota}, \chi^{\iota})})= {\prod_{w\vert v}\gamma(\iota\mathrm{WD}[V^{+}_{\pi, v|G_{E, w}} \otimes V_{\chi, w}], \psi_{E,w})^{-1} \over \gamma(\iota\mathrm{WD}[\mathrm{ad}(V_{\pi,v})(1)^{++}], \psi_{v})^{-1}} \cdot \mathscr{L}( V_{(\pi^{\iota}, \chi^{\iota}),v})^{-1}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \qquad e_{v}(V_{(\pi^{\iota}, \chi^{\iota})})= {\prod_{w\vert v}\gamma(\iota\mathrm{WD}[V^{+}_{\pi, v|G_{E, w}} \otimes V_{\chi, w}], \psi_{E,w})^{-1} \over \gamma(\iota\mathrm{WD}[\mathrm{ad}(V_{\pi,v})(1)^{++}], \psi_{v})^{-1}} \cdot \mathscr{L}( V_{(\pi^{\iota}, \chi^{\iota}),v})^{-1}, \end{aligned}\end{align} $$
where
![]() $\iota \mathrm {WD}$
is the functor from potentially semistable Galois representations to complex Weil–Deligne representations of [Reference FontaineFon94], the inverse Deligne–Langlands
$\iota \mathrm {WD}$
is the functor from potentially semistable Galois representations to complex Weil–Deligne representations of [Reference FontaineFon94], the inverse Deligne–Langlands
![]() $\gamma $
-factor is
$\gamma $
-factor is
![]() $\gamma (W, \psi _{v})^{-1} = {L(W)/ \varepsilon (W, \psi _{v}) L(W^{*}(1))}$
,Footnote
6
and
$\gamma (W, \psi _{v})^{-1} = {L(W)/ \varepsilon (W, \psi _{v}) L(W^{*}(1))}$
,Footnote
6
and
![]() $\psi _{E, w}=\psi _{v}\circ \mathrm {Tr}_{E_{w}/F_{v}}$
.
$\psi _{E, w}=\psi _{v}\circ \mathrm {Tr}_{E_{w}/F_{v}}$
.
Let
![]() $k_{0}\in \mathbf {Z}$
be such that the archimedean component of
$k_{0}\in \mathbf {Z}$
be such that the archimedean component of
![]() $\omega =\omega _{\pi }\omega _{\chi }$
is
$\omega =\omega _{\pi }\omega _{\chi }$
is
![]() $\omega _{\infty }(x)=x^{k_{0}}$
. We define
$\omega _{\infty }(x)=x^{k_{0}}$
. We define
and
1.1.4 Hida families
Let
![]() $U_{\mathrm {G}}^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
be any open compact subgroup, and for
$U_{\mathrm {G}}^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
be any open compact subgroup, and for
![]() $R=\mathbf {Z}_{p}, \mathbf {Q}_{p}$
, let
$R=\mathbf {Z}_{p}, \mathbf {Q}_{p}$
, let
![]() $\mathbf {T}^{\mathrm {sph,\ \mathrm {ord}}}_{U_{\mathrm {G}}^{p}, R}$
be the p-(nearly) ordinary spherical Hecke R-algebra acting on ordinary p-adic modular cuspforms for
$\mathbf {T}^{\mathrm {sph,\ \mathrm {ord}}}_{U_{\mathrm {G}}^{p}, R}$
be the p-(nearly) ordinary spherical Hecke R-algebra acting on ordinary p-adic modular cuspforms for
![]() $\mathrm {G}$
of tame level
$\mathrm {G}$
of tame level
![]() $U_{\mathrm {G}}^{p}$
.
$U_{\mathrm {G}}^{p}$
.
A cuspidal Hida family
![]() $\mathscr {X}_{\mathrm {G}}$
is an irreducible component of the space
$\mathscr {X}_{\mathrm {G}}$
is an irreducible component of the space
![]() $\mathscr {Y}_{\mathrm {G}, U_{\mathrm {G}}^{p}}:=\mathrm {Spec}\, \mathbf {T}_{U_{\mathrm {G}}^{p}, \mathbf {Q}_{p}}^{\mathrm {sph,\ \mathrm {ord}}}$
for some
$\mathscr {Y}_{\mathrm {G}, U_{\mathrm {G}}^{p}}:=\mathrm {Spec}\, \mathbf {T}_{U_{\mathrm {G}}^{p}, \mathbf {Q}_{p}}^{\mathrm {sph,\ \mathrm {ord}}}$
for some
![]() $U_{\mathrm {G}}^{p}$
. It is a scheme finite flat over
$U_{\mathrm {G}}^{p}$
. It is a scheme finite flat over
![]() (where
(where
![]() $\delta _{F, p}$
is the p-Leopoldt defect of F), coming with a dense ind-finite subscheme
$\delta _{F, p}$
is the p-Leopoldt defect of F), coming with a dense ind-finite subscheme
of classical points, and a locally free sheaf
![]() $\mathscr {V}_{\mathrm {G}}$
of rank
$\mathscr {V}_{\mathrm {G}}$
of rank
![]() $2$
endowed with an
$2$
endowed with an
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}}}$
-linear action of
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}}}$
-linear action of
![]() $G_{F}$
. To each
$G_{F}$
. To each
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
is associated an automorphic representation
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
is associated an automorphic representation
![]() $\pi _{x}$
of
$\pi _{x}$
of
![]() $\mathrm {G}(\mathbf {A}^{\infty })$
over
$\mathrm {G}(\mathbf {A}^{\infty })$
over
![]() $\mathbf {Q}_{p}(x)$
, and the fiber
$\mathbf {Q}_{p}(x)$
, and the fiber
![]() $\mathscr {V}_{\mathrm {G} |x}\cong V_{\pi _{x}}$
. The (numerical) weight of x is defined to be the weight of
$\mathscr {V}_{\mathrm {G} |x}\cong V_{\pi _{x}}$
. The (numerical) weight of x is defined to be the weight of
![]() $\pi _{x}$
.
$\pi _{x}$
.
Let
![]() $U^{p}_{\mathrm {H}}\subset \mathrm {H}(\mathbf {A}^{p\infty })$
be an open compact subgroup. We define
$U^{p}_{\mathrm {H}}\subset \mathrm {H}(\mathbf {A}^{p\infty })$
be an open compact subgroup. We define
where the topology on
![]() $\mathrm {H}(F)\backslash \mathrm {H}(\mathbf {A}^{p\infty })/U_{\mathrm {H}}^{p}$
is profinite; it comes with a universal character
$\mathrm {H}(F)\backslash \mathrm {H}(\mathbf {A}^{p\infty })/U_{\mathrm {H}}^{p}$
is profinite; it comes with a universal character
![]() $\chi _{\mathrm {univ}}\colon \mathrm {H}(F)\backslash \mathrm {H}(\mathbf {A}^{\infty })\to \mathscr {O}(\mathscr {Y}_{\mathrm {H}})^{\times }$
, identified with a
$\chi _{\mathrm {univ}}\colon \mathrm {H}(F)\backslash \mathrm {H}(\mathbf {A}^{\infty })\to \mathscr {O}(\mathscr {Y}_{\mathrm {H}})^{\times }$
, identified with a
![]() $G_{E}$
-representation
$G_{E}$
-representation
![]() $\mathscr {V}_{\mathrm {H}}$
of rank
$\mathscr {V}_{\mathrm {H}}$
of rank
![]() $1$
, and a dense ind-finite subscheme
$1$
, and a dense ind-finite subscheme
![]() $\mathscr {Y}_{\mathrm {H}}^{\mathrm { cl}}\subset \mathscr {Y}_{\mathrm {H}}$
, whose points y correspond to
$\mathscr {Y}_{\mathrm {H}}^{\mathrm { cl}}\subset \mathscr {Y}_{\mathrm {H}}$
, whose points y correspond to
![]() $U_{ \mathrm {H}}^{p}$
-invariant locally algebraic Hecke characters
$U_{ \mathrm {H}}^{p}$
-invariant locally algebraic Hecke characters
![]() $\chi _{y}$
of
$\chi _{y}$
of
![]() $\mathrm {H}$
over
$\mathrm {H}$
over
![]() $\mathbf {Q}_{p}(y)$
. The weight of y is defined to be the weight of
$\mathbf {Q}_{p}(y)$
. The weight of y is defined to be the weight of
![]() $\chi _{y}$
.
$\chi _{y}$
.
Finally, the ordinary eigenvariety for
![]() $\mathrm {G}\times \mathrm {H}$
of level
$\mathrm {G}\times \mathrm {H}$
of level
![]() $U^{p}_{\mathrm {G}}\times U^{p}_{\mathrm {H}}$
is
$U^{p}_{\mathrm {G}}\times U^{p}_{\mathrm {H}}$
is
Its subset of classical points is
![]() $\mathscr {Y}_{\mathrm {G}\times \mathrm {H}}^{\mathrm {cl}}:=\mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}\times \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}$
. A Hida family for
$\mathscr {Y}_{\mathrm {G}\times \mathrm {H}}^{\mathrm {cl}}:=\mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}\times \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}$
. A Hida family for
![]() $\mathrm {G}\times \mathrm {H}$
is an irreducible component of
$\mathrm {G}\times \mathrm {H}$
is an irreducible component of
![]() $\mathscr {Y}_{\mathrm {G}\times \mathrm {H}, U^{p}_{\mathrm {G}}\times U^{p}_{\mathrm {H}}}$
for some
$\mathscr {Y}_{\mathrm {G}\times \mathrm {H}, U^{p}_{\mathrm {G}}\times U^{p}_{\mathrm {H}}}$
for some
![]() $U^{p}_{\mathrm {G}}$
,
$U^{p}_{\mathrm {G}}$
,
![]() $U^{p}_{\mathrm {H}}$
.
$U^{p}_{\mathrm {H}}$
.
We now isolate an interesting subspace of
![]() $\mathscr {Y}_{\mathrm {G}\times \mathrm {H}}$
. Let
$\mathscr {Y}_{\mathrm {G}\times \mathrm {H}}$
. Let
![]() $\omega _{\mathrm {G}}\colon F^{\times }\backslash \mathbf {A}^{\infty , \times }\to \mathscr {O}(\mathscr {Y}_{\mathrm {G}})^{\times }$
be the character giving the action of the center of
$\omega _{\mathrm {G}}\colon F^{\times }\backslash \mathbf {A}^{\infty , \times }\to \mathscr {O}(\mathscr {Y}_{\mathrm {G}})^{\times }$
be the character giving the action of the center of
![]() $\mathrm {G}(\mathbf {A})$
on p-adic modular forms, let
$\mathrm {G}(\mathbf {A})$
on p-adic modular forms, let
![]() $\omega _{\mathrm {H}}:=\chi _{\mathrm {univ|\mathbf {A}^{\infty , \times }}}$
, and let
$\omega _{\mathrm {H}}:=\chi _{\mathrm {univ|\mathbf {A}^{\infty , \times }}}$
, and let
The self-dual locus
is the closed subspace defined by
![]() $\omega =\mathbf {1}$
. If
$\omega =\mathbf {1}$
. If
![]() $\mathscr {X}$
is a Hida family for
$\mathscr {X}$
is a Hida family for
![]() $\mathrm {G}\times \mathrm {H}$
, we denote
$\mathrm {G}\times \mathrm {H}$
, we denote
![]() $\mathscr {X}^{\mathrm {cl}}:= \mathscr {X}\cap \mathscr {Y}_{\mathrm {G}\times \mathrm {H}}^{\mathrm {cl}}$
,
$\mathscr {X}^{\mathrm {cl}}:= \mathscr {X}\cap \mathscr {Y}_{\mathrm {G}\times \mathrm {H}}^{\mathrm {cl}}$
,
![]() $\mathscr {X}^{\mathrm {sd}} := \mathscr {X}\cap \mathscr {Y}_{\mathrm {G}\times \mathrm {H}}^{\mathrm {sd}}$
, and
$\mathscr {X}^{\mathrm {sd}} := \mathscr {X}\cap \mathscr {Y}_{\mathrm {G}\times \mathrm {H}}^{\mathrm {sd}}$
, and
![]() $\mathscr {X}^{\mathrm {cl}, \mathrm {sd}}:= \mathscr {X}^{\mathrm {cl}}\cap \mathscr {X}^{\mathrm {sd}}$
.
$\mathscr {X}^{\mathrm {cl}, \mathrm {sd}}:= \mathscr {X}^{\mathrm {cl}}\cap \mathscr {X}^{\mathrm {sd}}$
.
1.1.5 Main theorem
Throughout this paper, if
![]() $\mathscr {X}$
is a scheme over a characteristic-zero field L, we identify a geometric point
$\mathscr {X}$
is a scheme over a characteristic-zero field L, we identify a geometric point
![]() $x\in \mathscr {X}(\mathbf {C})$
with a pair
$x\in \mathscr {X}(\mathbf {C})$
with a pair
![]() $(x_{0}, \iota )$
, where
$(x_{0}, \iota )$
, where
![]() $x_{0}\in \mathscr {X}$
is the scheme point image of (as a synonym, underlying) x and
$x_{0}\in \mathscr {X}$
is the scheme point image of (as a synonym, underlying) x and
![]() $\iota \colon L(x_{0})\hookrightarrow \mathbf {C}$
is an embedding. If
$\iota \colon L(x_{0})\hookrightarrow \mathbf {C}$
is an embedding. If
![]() $\mathscr {X}$
is integral, we denote by
$\mathscr {X}$
is integral, we denote by
![]() $\mathscr {K}(\mathscr {X})$
the local ring of the generic point, which we call the field of meromorphic functions on
$\mathscr {K}(\mathscr {X})$
the local ring of the generic point, which we call the field of meromorphic functions on
![]() $\mathscr {X}$
.
$\mathscr {X}$
.
If
![]() $\mathscr {X}$
is a Hida family for
$\mathscr {X}$
is a Hida family for
![]() $\mathrm {G}\times \mathrm {H}$
, we define
$\mathrm {G}\times \mathrm {H}$
, we define
![]() $\mathscr {X}^{\mathrm {cl}, \mathrm {wt}}\subset \mathscr {X}^{\mathrm {cl}}$
to be the subset of points
$\mathscr {X}^{\mathrm {cl}, \mathrm {wt}}\subset \mathscr {X}^{\mathrm {cl}}$
to be the subset of points
![]() $(x_{0}, y_{0})$
whose contracted weight
$(x_{0}, y_{0})$
whose contracted weight
![]() $(k_{0}, w, l)$
satisfies
$(k_{0}, w, l)$
satisfies
We denote
![]() $\mathscr {X}^{\mathrm {cl},\mathrm {sd}, \mathrm {wt}}:= \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}\cap \mathscr {X}^{\mathrm {cl}, \mathrm {wt}}$
.
$\mathscr {X}^{\mathrm {cl},\mathrm {sd}, \mathrm {wt}}:= \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}\cap \mathscr {X}^{\mathrm {cl}, \mathrm {wt}}$
.
Theorem A Let
![]() $\mathscr {X}$
be a Hida family for
$\mathscr {X}$
be a Hida family for
![]() $\mathrm {G}\times \mathrm {H}$
whose self-dual locus
$\mathrm {G}\times \mathrm {H}$
whose self-dual locus
![]() $\mathscr {X}^{\mathrm {sd}}$
is nonempty. There exists a unique meromorphic function
$\mathscr {X}^{\mathrm {sd}}$
is nonempty. There exists a unique meromorphic function
whose polar locus
![]() $\mathscr {D}$
does not intersect
$\mathscr {D}$
does not intersect
![]() $\mathscr {X}^{\mathrm {cl}, \mathrm {sd}, \mathrm {wt}}$
such that for each
$\mathscr {X}^{\mathrm {cl}, \mathrm {sd}, \mathrm {wt}}$
such that for each
![]() $(x, y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {wt}}(\mathbf {C})- \mathscr {D}(\mathbf {C})$
, we have
$(x, y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {wt}}(\mathbf {C})- \mathscr {D}(\mathbf {C})$
, we have
Here, if
![]() $(x_{0}, y_{0})\in \mathscr {X}^{\mathrm {cl}}$
is the point underlying
$(x_{0}, y_{0})\in \mathscr {X}^{\mathrm {cl}}$
is the point underlying
![]() $(x,y)$
and
$(x,y)$
and
![]() $\iota \colon \mathbf {Q}_{p}(x_{0}, y_{0}) \hookrightarrow \mathbf {C}$
is the corresponding embedding, we have denoted
$\iota \colon \mathbf {Q}_{p}(x_{0}, y_{0}) \hookrightarrow \mathbf {C}$
is the corresponding embedding, we have denoted
![]() $\pi _{x} =\pi _{x_{0}}^{\iota }, \chi _{y}=\chi _{y_{0}}^{\iota }$
, and the interpolation factor is as in (1.1.5).
$\pi _{x} =\pi _{x_{0}}^{\iota }, \chi _{y}=\chi _{y_{0}}^{\iota }$
, and the interpolation factor is as in (1.1.5).
The value of the interpolation factor agrees with the general conjectures of Coates and Perrin-Riou (see [Reference CoatesCoa91]). (The notation
![]() $\mathscr {V}$
is meant to evoke some “universal virtual Galois representation interpolating (1.1.3).”)
$\mathscr {V}$
is meant to evoke some “universal virtual Galois representation interpolating (1.1.3).”)
1.1.6 Previous related work
When
![]() $E/F$
splits above p, Theorem A may be essentially deduced from the main result of [Reference HidaHid91] (see also [Reference HidaHid09]). Hida’s method uses the Rankin–Selberg integral, whereas ours uses Waldspurger’s variant [Reference WaldspurgerWal85] based on the Weil representation (as discussed below).
$E/F$
splits above p, Theorem A may be essentially deduced from the main result of [Reference HidaHid91] (see also [Reference HidaHid09]). Hida’s method uses the Rankin–Selberg integral, whereas ours uses Waldspurger’s variant [Reference WaldspurgerWal85] based on the Weil representation (as discussed below).
The numerator of our L-value is a special case of the standard L-function for
![]() $\mathrm {GL}_{2}\times \mathrm {GL}_{1}$
over E, and when so considered, our p-adic L-function is a multiple of the restriction to some base-change locus of one constructed by Januszewski [Reference JanuszewskiJan] using the method of modular symbols; however, that function is not uniquely characterized by its interpolation property, which involves unspecified periods.
$\mathrm {GL}_{2}\times \mathrm {GL}_{1}$
over E, and when so considered, our p-adic L-function is a multiple of the restriction to some base-change locus of one constructed by Januszewski [Reference JanuszewskiJan] using the method of modular symbols; however, that function is not uniquely characterized by its interpolation property, which involves unspecified periods.
Finally, when
![]() $F=\mathbf {Q}$
, variants of
$F=\mathbf {Q}$
, variants of
![]() $\mathscr {L}_{p}(\mathscr {V})$
were constructed by Hida [Reference HidaHid88, Theorem 5.1a] and, more recently, by Loeffler and Büyükboduk and Lei (see [Reference Büyükboduk and LeiBL, Section B.4]) under various local restrictions.
$\mathscr {L}_{p}(\mathscr {V})$
were constructed by Hida [Reference HidaHid88, Theorem 5.1a] and, more recently, by Loeffler and Büyükboduk and Lei (see [Reference Büyükboduk and LeiBL, Section B.4]) under various local restrictions.
1.2 Idea of proof, organization of the paper, and discussion of the method
The proof combines the strategy of Hida [Reference HidaHid91] with an enhanced version of that of [Reference DisegniDis17, Proof of Theorem A], where we had constructed the “slices”
![]() $\mathscr {L}_{p}(\mathscr {V})(x, -)$
for
$\mathscr {L}_{p}(\mathscr {V})(x, -)$
for
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
of weight
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
of weight
![]() $2$
.
$2$
.
We start from Waldspurger’s [Reference WaldspurgerWal85] integral representation of Rankin–Selberg type
where
![]() $( \ , \ )$
is a normalized Petersson product, f is a form in
$( \ , \ )$
is a normalized Petersson product, f is a form in
![]() $\pi $
with Whittaker function
$\pi $
with Whittaker function
![]() $\otimes _{v}W_{v}$
, the form
$\otimes _{v}W_{v}$
, the form
![]() $I(\phi , \chi )$
is a mixed theta-Eisenstein series depending on a certain Schwartz function
$I(\phi , \chi )$
is a mixed theta-Eisenstein series depending on a certain Schwartz function
![]() $\phi $
, and the
$\phi $
, and the
![]() $R_{v}$
are normalized local integrals.
$R_{v}$
are normalized local integrals.
In Section 2, we discuss the general setup. In Section 3, we make a judicious choice of
![]() $\phi _{v}$
at the places
$\phi _{v}$
at the places
![]() $v\vert p\infty $
and interpolate the ordinary projection of
$v\vert p\infty $
and interpolate the ordinary projection of
![]() ${I}(\phi , \chi )$
into a
${I}(\phi , \chi )$
into a
![]() $\mathscr {Y}_{\mathrm {G}\times \mathrm {H}}$
-adic modular form. In Section 4, we interpolate
$\mathscr {Y}_{\mathrm {G}\times \mathrm {H}}$
-adic modular form. In Section 4, we interpolate
![]() $R_{v}$
for
$R_{v}$
for
![]() $v\nmid p\infty $
using sheaves of local Whittaker functions over
$v\nmid p\infty $
using sheaves of local Whittaker functions over
![]() $\mathscr {X}$
provided by the local Langlands correspondence in families (Section 4.4); we compute
$\mathscr {X}$
provided by the local Langlands correspondence in families (Section 4.4); we compute
![]() $R_{v}$
for
$R_{v}$
for
![]() $v\vert p\infty $
(Section 4.3), which yield the interpolation factors in (1.1.8); and finally (Section 4.5), we use (1.2.1) to define
$v\vert p\infty $
(Section 4.3), which yield the interpolation factors in (1.1.8); and finally (Section 4.5), we use (1.2.1) to define
![]() $\mathscr {L}_{p}(\mathscr {V})$
as a glued quotient of the global and local (away from
$\mathscr {L}_{p}(\mathscr {V})$
as a glued quotient of the global and local (away from
![]() $p\infty $
) families of zeta integrals.
$p\infty $
) families of zeta integrals.
In Appendix A, we give a TV-inspired bijective proof of a combinatorial lemma occurring in Section 3.3.
The method of constructing p-adic L-functions as ratios of arbitrary matching families of global and local zeta integrals should be applicable whenever an integral representation for the corresponding complex L-function is available, at least if the groups involved are products of general linear groups: for example, for Rankin–Selberg L-functions. It can be compared to the “hard” constructions from much of the existing literature on p-adic L-functions, which rely on fine choices of local data at all places, computation of the associated integrals, and bounds on the ramification of the data (see [Reference HsiehHsi21] for an excellent example of the state of the art). To be sure, the two approaches should be viewed as complementary rather than alternative: while the “soft” construction provides a flexibility useful for some applications (such as in [Reference DisegniDis17]), explicit choices and computations can still be plugged into it, and are likely still indispensable to address finer issues such as integrality.
For another brief general discussion of our method focused on the role of the local Langlands correspondence in families (LLCF), as well as some results on local interpolation, we refer to [Reference DisegniDis20, Sections 1.2 and 5];Footnote 7 see also the very recent work of Cai and Fan [Reference Cai, Shu and TianCF] for a related study in the context of periods attached to spherical varieties. Abelian antecedents of the construction, for which the LLCF is not needed, can be found in [Dis17, Reference Liu, Zhang and ZhangLZZ18].
The local–global approach may in principle introduce poles coming from zeros of the families of local integrals. In our specific setup, the Waldspurger local integrals are not easy to control (at least for this author) away from the self-dual locus. This is why Theorem A, while sufficient for the arithmetic applications in [Reference DisegniDis/b], is not as strong as it could be: one may at least expect that the condition that
![]() $\mathscr {X}^{\mathrm {sd}}$
be nonempty is superfluous, and that the polar locus of
$\mathscr {X}^{\mathrm {sd}}$
be nonempty is superfluous, and that the polar locus of
![]() $\mathscr {L}_{p}(\mathscr {V})$
should not intersect
$\mathscr {L}_{p}(\mathscr {V})$
should not intersect
![]() $\mathscr {X}^{\mathrm {cl}, \mathrm {wt}}$
. As noted by a referee, approaching
$\mathscr {X}^{\mathrm {cl}, \mathrm {wt}}$
. As noted by a referee, approaching
![]() $\mathscr {L}_{p}(\mathscr {V})$
via the well-understood Rankin–Selberg integrals for
$\mathscr {L}_{p}(\mathscr {V})$
via the well-understood Rankin–Selberg integrals for
![]() $\mathrm {GL}_{2}\times \mathrm {GL}_{2}$
would likely yield such a strengthening.
$\mathrm {GL}_{2}\times \mathrm {GL}_{2}$
would likely yield such a strengthening.
2 p-adic modular forms and Hida families
The material of this section is largely due to Hida (see [Reference HidaHid91, Sections 1–3 and 7] and the references therein).
2.1 Notation and preliminaries
The notation introduced in the present subsection (or in the introduction) will be used throughout the paper unless otherwise noted, in particular, the groups
![]() $\mathrm {G}$
and
$\mathrm {G}$
and
![]() $\mathrm {H}$
defined in (1.1.1).
$\mathrm {H}$
defined in (1.1.1).
2.1.1 General notation
The following notational choices are largely standard.
-
• The fields F and E are as fixed in the introduction unless specified otherwise; if
 $*$
denotes a place of
$*$
denotes a place of
 $\mathbf {Q}$
or a finite set thereof, we denote by
$\mathbf {Q}$
or a finite set thereof, we denote by
 $S_{*}$
the set of places of F above
$S_{*}$
the set of places of F above
 $*$
.
$*$
. -
• We denote by
 $D_{F}$
,
$D_{F}$
,
 $D_{E}$
, and
$D_{E}$
, and
 $D_{E/F}$
, respectively, the absolute discriminants of F and E and relative discriminant of
$D_{E/F}$
, respectively, the absolute discriminants of F and E and relative discriminant of
 $E/F$
; for a finite place v of F, we denote by
$E/F$
; for a finite place v of F, we denote by
 $d_{v}\in F_{v}$
a generator of the different ideal of F and by
$d_{v}\in F_{v}$
a generator of the different ideal of F and by
 $D_{v}\in F_{v}$
a generator of the relative discriminant ideal.
$D_{v}\in F_{v}$
a generator of the relative discriminant ideal. -
• We denote by
 $<$
the partial order on F given by
$<$
the partial order on F given by
 $x<y$
if and only if
$x<y$
if and only if
 $\tau (x)<\tau (y)$
for all
$\tau (x)<\tau (y)$
for all
 $\tau \in \Sigma _{\infty }$
; we denote
$\tau \in \Sigma _{\infty }$
; we denote
 $\mathbf {R}^{+}:= \{x\in \mathbf {R}\, | \, x>0\}$
and
$\mathbf {R}^{+}:= \{x\in \mathbf {R}\, | \, x>0\}$
and
 $F^{+}:=\{x\in F\, |\, x>0\}\subset F^{\times }$
.
$F^{+}:=\{x\in F\, |\, x>0\}\subset F^{\times }$
. -
•
 $\mathbf {A}$
is the ring of adèles of F; if S is a finite set of places of a number field F, we denote
$\mathbf {A}$
is the ring of adèles of F; if S is a finite set of places of a number field F, we denote
 $\mathbf {A}^{S}=\prod ^{\prime }_{v\notin S} F_{v}$
, and
$\mathbf {A}^{S}=\prod ^{\prime }_{v\notin S} F_{v}$
, and
 $F_{S}:= \prod _{v\in S}F_{v}$
; when S consists of the set of places of F above some finite set of places of
$F_{S}:= \prod _{v\in S}F_{v}$
; when S consists of the set of places of F above some finite set of places of
 $\mathbf {Q}$
(for instance, the place p), we use the same notation with those places of
$\mathbf {Q}$
(for instance, the place p), we use the same notation with those places of
 $\mathbf {Q}$
instead of S (for instance,
$\mathbf {Q}$
instead of S (for instance,
 $F_{p}=F_{S_{p}}$
). We denote
$F_{p}=F_{S_{p}}$
). We denote
 $F_{\infty }^{+}=\{x\in F_{\infty }\ | \ x_{\tau }>0 \text { for all}\ \tau \in \Sigma _{\infty }\}$
and
$F_{\infty }^{+}=\{x\in F_{\infty }\ | \ x_{\tau }>0 \text { for all}\ \tau \in \Sigma _{\infty }\}$
and
 $\mathbf {A}^{+}:=\mathbf {A}^{\infty }\times F_{\infty }^{+}$
.
$\mathbf {A}^{+}:=\mathbf {A}^{\infty }\times F_{\infty }^{+}$
. -
• We denote by
 $\psi \colon F\backslash \mathbf {A}\to \mathbf {C}^{\times }$
the standard additive character as in Section 1.1.3.
$\psi \colon F\backslash \mathbf {A}\to \mathbf {C}^{\times }$
the standard additive character as in Section 1.1.3. -
• If
 $R/R_{0}$
is a ring extension, A is an
$R/R_{0}$
is a ring extension, A is an
 $R_{0}$
-algebra, and X is an
$R_{0}$
-algebra, and X is an
 $R_{0}$
-scheme, we denote
$R_{0}$
-scheme, we denote  $$ \begin{align*}A_{R}:=A\otimes_{R_{0}}R, \qquad X_{R}:= X\times_{\mathrm{Spec}\, R_{0}}R.\end{align*} $$
$$ \begin{align*}A_{R}:=A\otimes_{R_{0}}R, \qquad X_{R}:= X\times_{\mathrm{Spec}\, R_{0}}R.\end{align*} $$
-
• We denote by
 $G_{K}$
the absolute Galois group of a field K.
$G_{K}$
the absolute Galois group of a field K. -
• If K is a finite extension of F, its class number is denoted by
 $$ \begin{align*}h_{K}:= |K^{\times}\backslash \mathbf{A}_{K}^{\infty, \times}/\widehat{\mathscr{O}}^{\times}_{K}|.\end{align*} $$
$$ \begin{align*}h_{K}:= |K^{\times}\backslash \mathbf{A}_{K}^{\infty, \times}/\widehat{\mathscr{O}}^{\times}_{K}|.\end{align*} $$
-
• For a place v of F, we denote by
 $\varpi _{v}$
a fixed uniformizer at v, and by
$\varpi _{v}$
a fixed uniformizer at v, and by
 $q_{F,v} $
the cardinality of the residue field; we denote
$q_{F,v} $
the cardinality of the residue field; we denote
 $q_{F, p}:=(q_{F, v})_{v\in S_{p}}$
.
$q_{F, p}:=(q_{F, v})_{v\in S_{p}}$
. -
• The class field theory isomorphism is normalized by sending uniformizers to geometric Frobenii; for K a number field (respectively, a local field), we will then identify characters of
 $G_{K}$
with characters of
$G_{K}$
with characters of
 $K^{\times }\backslash {\mathbf {A}}_{K}^{\times }$
(respectively,
$K^{\times }\backslash {\mathbf {A}}_{K}^{\times }$
(respectively,
 $K^{\times })$
without further comment.
$K^{\times })$
without further comment. -
• If I is a finite index set and
 $x=(x_{i})_{i}$
,
$x=(x_{i})_{i}$
,
 $y=(y_{i})$
are real vectors, we define
$y=(y_{i})$
are real vectors, we define
 $(xy)_{i}=x_{i}y_{i}$
and
$(xy)_{i}=x_{i}y_{i}$
and
 $x^{y}:= \prod _{i}x_{i}^{y_{i}} $
whenever that makes sense. Moreover, we often identify an integer
$x^{y}:= \prod _{i}x_{i}^{y_{i}} $
whenever that makes sense. Moreover, we often identify an integer
 $w_{0}$
with the constant vector
$w_{0}$
with the constant vector
 $(w_{0})_{i\in I}\in \mathbf {Z}^{I}$
.
$(w_{0})_{i\in I}\in \mathbf {Z}^{I}$
. -
• We denote by
 $\mathbf {1}[\cdot ]$
the
$\mathbf {1}[\cdot ]$
the
 $\{0, 1\}$
-valued function on logical propositions such that
$\{0, 1\}$
-valued function on logical propositions such that
 $\mathbf {1}[\phi ]=1$
if and only if
$\mathbf {1}[\phi ]=1$
if and only if
 $\phi $
is true.
$\phi $
is true.
2.1.2 Subgroups of
 $\mathrm {GL}_{2}$
and special elements
$\mathrm {GL}_{2}$
and special elements
We denote by Z, A, and N, respectively the center, diagonal torus, and upper unipotent subgroup of
![]() $\mathrm {G}=\mathrm {GL}_{2/F}$
; we let
$\mathrm {G}=\mathrm {GL}_{2/F}$
; we let
![]() $P=AN$
and
$P=AN$
and
![]() $P^{1}:=P\cap \mathrm {SL}_{2/F}$
. We define a map
$P^{1}:=P\cap \mathrm {SL}_{2/F}$
. We define a map
![]() $\mathbf {a}\colon \mathrm {GL}_{1/F}\to \mathrm {G}$
by
$\mathbf {a}\colon \mathrm {GL}_{1/F}\to \mathrm {G}$
by
 $$ \begin{align*}\mathbf{a}(y):= \left(\begin{array}{cc}y&\\&1\end{array}\right).\end{align*} $$
$$ \begin{align*}\mathbf{a}(y):= \left(\begin{array}{cc}y&\\&1\end{array}\right).\end{align*} $$
We denote
 $$ \begin{align*}w:= \left(\begin{array}{cc}&1\\-1&\end{array}\right)\in \mathrm{GL}_{2}(F)\end{align*} $$
$$ \begin{align*}w:= \left(\begin{array}{cc}&1\\-1&\end{array}\right)\in \mathrm{GL}_{2}(F)\end{align*} $$
or its image in
![]() $\mathrm {GL}_{2}(R)$
for any F-algebra R. (The context will prevent any confusion with the notation for the weights of
$\mathrm {GL}_{2}(R)$
for any F-algebra R. (The context will prevent any confusion with the notation for the weights of
![]() $\mathrm {G}$
.) For
$\mathrm {G}$
.) For
![]() $r\in \mathbf {Z}_{\geq 1}^{S_{p}}$
, we define
$r\in \mathbf {Z}_{\geq 1}^{S_{p}}$
, we define
 $$ \begin{align*}w_{r_{v},v}:= \left(\begin{array}{cc}&1\\-\varpi_{v}^{r_{v}}&\end{array}\right)\in \mathrm{GL}_{2}(F_{v}), \qquad w_{r, p}:= \prod_{v\vert p} w_{r_{v},v}\in \mathrm{GL}_{2}(F_{p}),\end{align*} $$
$$ \begin{align*}w_{r_{v},v}:= \left(\begin{array}{cc}&1\\-\varpi_{v}^{r_{v}}&\end{array}\right)\in \mathrm{GL}_{2}(F_{v}), \qquad w_{r, p}:= \prod_{v\vert p} w_{r_{v},v}\in \mathrm{GL}_{2}(F_{p}),\end{align*} $$
as well as a sequence of compact subgroups
 $$ \begin{align*} U_{v, r_{v}}:=U^{1}_{1}(\varpi_{v}^{r_{v}}) &:= \{ \left(\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\right) \in \mathrm{GL}_{2}(\mathscr{O}_{F,v})\, :\, a-1\equiv d-1 \equiv c\equiv 0 \pmod{\varpi_{v}^{r_{v}}}\}\subset \mathrm{GL}_{2}(F_{v}),\\[5pt]U_{p, r}&:= \prod_{v\in S_{p}} U_{v, r_{v}}. \end{align*} $$
$$ \begin{align*} U_{v, r_{v}}:=U^{1}_{1}(\varpi_{v}^{r_{v}}) &:= \{ \left(\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\right) \in \mathrm{GL}_{2}(\mathscr{O}_{F,v})\, :\, a-1\equiv d-1 \equiv c\equiv 0 \pmod{\varpi_{v}^{r_{v}}}\}\subset \mathrm{GL}_{2}(F_{v}),\\[5pt]U_{p, r}&:= \prod_{v\in S_{p}} U_{v, r_{v}}. \end{align*} $$
For
![]() $\theta \in (\mathbf {R}/2\pi \mathbf {Z})^{S_{\infty }}$
, we denote
$\theta \in (\mathbf {R}/2\pi \mathbf {Z})^{S_{\infty }}$
, we denote
 $r_{\theta }:=\left ( \left (\begin {array}{cc}\cos \theta _{v} &\sin \theta _{v}\\-\sin \theta _{v}&\cos \theta _{v}\end {array}\right )\right )_{v}\in \mathrm {SO}(2, F_{\infty }).$
$r_{\theta }:=\left ( \left (\begin {array}{cc}\cos \theta _{v} &\sin \theta _{v}\\-\sin \theta _{v}&\cos \theta _{v}\end {array}\right )\right )_{v}\in \mathrm {SO}(2, F_{\infty }).$
2.1.3 Hecke algebras
Let S be a finite set of non-archimedean places of F, and let
![]() $U^{S}=\prod _{v\notin S}U_{v}\subset \mathrm {GL}_{2}(\mathbf {A}^{S\infty })$
be an open compact subgroup. For each finite set of finite places S, we define the Hecke algebra
$U^{S}=\prod _{v\notin S}U_{v}\subset \mathrm {GL}_{2}(\mathbf {A}^{S\infty })$
be an open compact subgroup. For each finite set of finite places S, we define the Hecke algebra
It carries an involution
arising from the map
![]() $g\mapsto g^{-1}$
on the group
$g\mapsto g^{-1}$
on the group
![]() $\mathrm {G}$
.
$\mathrm {G}$
.
Let
![]() $A_{p}:= A(F_{p})\subset \mathrm {G}(F_{p})$
be the diagonal torus, and let
$A_{p}:= A(F_{p})\subset \mathrm {G}(F_{p})$
be the diagonal torus, and let
![]() $A_{p}^{+}$
be the set of
$A_{p}^{+}$
be the set of
![]() $t=\left (\begin {smallmatrix}t_{1}& \\&{t_{2}}\end {smallmatrix}\right ) $
such that
$t=\left (\begin {smallmatrix}t_{1}& \\&{t_{2}}\end {smallmatrix}\right ) $
such that
![]() $v(t_{1}) \geq v(t_{2})$
for all
$v(t_{1}) \geq v(t_{2})$
for all
![]() $v\vert p$
. The involution
$v\vert p$
. The involution
preserves
![]() $A_{p}^{+}$
. For S a finite set of places of F disjoint from
$A_{p}^{+}$
. For S a finite set of places of F disjoint from
![]() $S_{p}\cup S_{\infty }$
, we define the ordinary Hecke algebra
$S_{p}\cup S_{\infty }$
, we define the ordinary Hecke algebra
over
![]() $\mathbf {Z}_{p}$
, which will act on spaces of ordinary modular forms (here and in the rest of the text, a subscript
$\mathbf {Z}_{p}$
, which will act on spaces of ordinary modular forms (here and in the rest of the text, a subscript
![]() $Sp$
is shorthand for
$Sp$
is shorthand for
![]() $S\cup S_{p}$
). It is endowed with the involution
$S\cup S_{p}$
). It is endowed with the involution
![]() $\curlyvee $
deduced from (2.1.1) and (2.1.2).
$\curlyvee $
deduced from (2.1.1) and (2.1.2).
If
![]() $U=\prod _{v}U_{v}\subset \mathrm {G}(\mathbf {A}^{\infty })$
(respectively,
$U=\prod _{v}U_{v}\subset \mathrm {G}(\mathbf {A}^{\infty })$
(respectively,
![]() $U^{p}=\prod _{v\nmid p}U_{v}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
) are open compact subgroups, and S (respectively,
$U^{p}=\prod _{v\nmid p}U_{v}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
) are open compact subgroups, and S (respectively,
![]() $S^{p}$
) is the set of places such that
$S^{p}$
) is the set of places such that
![]() $U_{v}$
is not maximal, we define
$U_{v}$
is not maximal, we define
(These depend on S, but their images in endomorphisms rings of spaces of modular forms do not.)
2.1.4 Measures
We use the same notation and conventions for Haar measures and integration as in [Reference Yuan, Zhang and ZhangYZZ12, Section 1.6] and [Reference DisegniDis17, Section 1.9]. In particular, we have a regularized integration functional
which satisfies the following.
Lemma 2.1 Let f be a smooth function on
![]() $\mathbf {A}_{E}^{\times }$
that is invariant under
$\mathbf {A}_{E}^{\times }$
that is invariant under
![]() $E_{\infty }^{\times }$
. Let
$E_{\infty }^{\times }$
. Let
![]() $\mu \subset \mathscr {O}_{E}^{\times }$
be a finite index subgroup fixing f (under the scaling action). Then
$\mu \subset \mathscr {O}_{E}^{\times }$
be a finite index subgroup fixing f (under the scaling action). Then
 $$ \begin{align*}\int^{*}_{E^{\times}\backslash {\mathbf{A}}_{E}^{\times} /\mathbf{A}^{\times}} \sum_{x\in E^{\times}} f(xt) \, dt = { 2L(1,\eta)\over h_{E}^{}} { [\mathscr{O}_{E}^{\times}:\mu_{}] } \int_{ \mathbf{A}_{E}^{\infty, \times}} \sum_{\alpha\in \mu_{}} f(\alpha t)\, d^{\bullet}t,\end{align*} $$
$$ \begin{align*}\int^{*}_{E^{\times}\backslash {\mathbf{A}}_{E}^{\times} /\mathbf{A}^{\times}} \sum_{x\in E^{\times}} f(xt) \, dt = { 2L(1,\eta)\over h_{E}^{}} { [\mathscr{O}_{E}^{\times}:\mu_{}] } \int_{ \mathbf{A}_{E}^{\infty, \times}} \sum_{\alpha\in \mu_{}} f(\alpha t)\, d^{\bullet}t,\end{align*} $$
where
![]() $d^{\bullet } t $
is the Haar measure giving volume
$d^{\bullet } t $
is the Haar measure giving volume
![]() $1$
to
$1$
to
![]() $ \widehat {\mathscr {O}}^{\times }_{E}$
.
$ \widehat {\mathscr {O}}^{\times }_{E}$
.
Proof Let
![]() $U\subset \mathbf {A}_{E}^{\infty , \times }$
be any compact open subgroup fixing f. Since both sides are independent of
$U\subset \mathbf {A}_{E}^{\infty , \times }$
be any compact open subgroup fixing f. Since both sides are independent of
![]() $\mu $
, we may assume that
$\mu $
, we may assume that
![]() $\mu = \mathscr {O}_{E}^{\times }\cap U$
. By [Reference Yuan, Zhang and ZhangYZZ12, equation (1.6.1) and the following paragraphs], we have
$\mu = \mathscr {O}_{E}^{\times }\cap U$
. By [Reference Yuan, Zhang and ZhangYZZ12, equation (1.6.1) and the following paragraphs], we have

Now, by a coset identity,
 $$ \begin{align*}|E^{\times}\backslash \mathbf{A}_{E}^{\infty, \times}/U | = h_{E} { |\widehat{\mathscr{O}}^{\times}_{E}/ U| \over [\mathscr{O}_{E}^{\times}:\mu_{}]},\end{align*} $$
$$ \begin{align*}|E^{\times}\backslash \mathbf{A}_{E}^{\infty, \times}/U | = h_{E} { |\widehat{\mathscr{O}}^{\times}_{E}/ U| \over [\mathscr{O}_{E}^{\times}:\mu_{}]},\end{align*} $$
and by [Reference Yuan, Zhang and ZhangYZZ12, Section 1.6.3],
![]() $\mathrm {vol} ({E^{\times }\backslash {\mathbf {A}}_{E}^{\times } /\mathbf {A}^{\times }})=2L(1, \eta )$
. Hence, (2.1.3) equals
$\mathrm {vol} ({E^{\times }\backslash {\mathbf {A}}_{E}^{\times } /\mathbf {A}^{\times }})=2L(1, \eta )$
. Hence, (2.1.3) equals
 $$ \begin{align*}{2L(1, \eta)\over h_{E}} { [\mathscr{O}_{E}^{\times}:\mu_{}] \over |\widehat{\mathscr{O}}^{\times}_{E}/ U|} \sum_{t\in E^{\times}\backslash \mathbf{A}_{E}^{\infty, \times}/U} f(t).\end{align*} $$
$$ \begin{align*}{2L(1, \eta)\over h_{E}} { [\mathscr{O}_{E}^{\times}:\mu_{}] \over |\widehat{\mathscr{O}}^{\times}_{E}/ U|} \sum_{t\in E^{\times}\backslash \mathbf{A}_{E}^{\infty, \times}/U} f(t).\end{align*} $$
If we compose with the operator
![]() $f(\cdot )\mapsto \sum _{x\in E^{\times }} f(x\cdot ) = \sum _{x\in \mu _{}\backslash E^{\times }} \sum _{\alpha \in \mu _{}} f(\alpha x\cdot )$
, we obtain
$f(\cdot )\mapsto \sum _{x\in E^{\times }} f(x\cdot ) = \sum _{x\in \mu _{}\backslash E^{\times }} \sum _{\alpha \in \mu _{}} f(\alpha x\cdot )$
, we obtain
 $$ \begin{align*}{ 2L(1,\eta)\over h_{E}^{}} { [\mathscr{O}_{E}^{\times}:\mu_{}] \over |\widehat{\mathscr{O}}^{\times}_{E}/ U|} \sum_{ t\in \mathbf{A}_{E}^{\infty, \times}/U} \sum_{\alpha\in \mu_{}}f(\alpha t) = { 2L(1,\eta)\over h_{E}^{}} { [\mathscr{O}_{E}^{\times}:\mu_{}] } \int_{ \mathbf{A}_{E}^{\infty, \times}} \sum_{\alpha\in \mu_{}} f(\alpha t)\, d^{\bullet} t .\end{align*} $$
$$ \begin{align*}{ 2L(1,\eta)\over h_{E}^{}} { [\mathscr{O}_{E}^{\times}:\mu_{}] \over |\widehat{\mathscr{O}}^{\times}_{E}/ U|} \sum_{ t\in \mathbf{A}_{E}^{\infty, \times}/U} \sum_{\alpha\in \mu_{}}f(\alpha t) = { 2L(1,\eta)\over h_{E}^{}} { [\mathscr{O}_{E}^{\times}:\mu_{}] } \int_{ \mathbf{A}_{E}^{\infty, \times}} \sum_{\alpha\in \mu_{}} f(\alpha t)\, d^{\bullet} t .\end{align*} $$
2.2 Modular forms and their q-expansions
Let
![]() $\frak h\subset \mathbf {C}$
be the upper half-plane. We view
$\frak h\subset \mathbf {C}$
be the upper half-plane. We view
![]() $\mathrm {G}(F_{\infty })$
as acting on
$\mathrm {G}(F_{\infty })$
as acting on
![]() $\frak h^{\Sigma _{\infty }}$
by Möbius transformations, and identify
$\frak h^{\Sigma _{\infty }}$
by Möbius transformations, and identify
with the neutral connected component of the stabilizer of
![]() $\mathrm {i} := (\sqrt {-1}, \ldots , \sqrt {-1})\in \frak h^{{\Sigma _{\infty }}}$
.
$\mathrm {i} := (\sqrt {-1}, \ldots , \sqrt {-1})\in \frak h^{{\Sigma _{\infty }}}$
.
2.2.1 Nearly holomorphic modular forms
Let
![]() $\underline {w}$
be an (
$\underline {w}$
be an (
![]() $\infty $
-adic Section 1.1.1) weight for
$\infty $
-adic Section 1.1.1) weight for
![]() $\mathrm {G}$
, let
$\mathrm {G}$
, let
![]() $U\subset \mathrm {G}(\mathbf {A}^{\infty })$
be a compact open subgroup, and let
$U\subset \mathrm {G}(\mathbf {A}^{\infty })$
be a compact open subgroup, and let
![]() $m=(m_{\tau })\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
. A complex nearly holomorphic (Hilbert) modular form of weight
$m=(m_{\tau })\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
. A complex nearly holomorphic (Hilbert) modular form of weight
![]() $\underline {w}$
, level U, and degree
$\underline {w}$
, level U, and degree
![]() $\leq m$
is a function
$\leq m$
is a function
satisfying the following two conditions:
-
(1) For all
 $g\in \mathrm {G}(\mathbf {A})$
,
$g\in \mathrm {G}(\mathbf {A})$
,
 $\gamma \in \mathrm {G}(F)$
, and
$\gamma \in \mathrm {G}(F)$
, and
 $k \in U C_{\infty }^{+}$
, where for
$k \in U C_{\infty }^{+}$
, where for $$ \begin{align*}f(\gamma g k) = j_{\underline{w}}(k_{\infty}, \mathrm{i})^{-1}f(g),\end{align*} $$
$$ \begin{align*}f(\gamma g k) = j_{\underline{w}}(k_{\infty}, \mathrm{i})^{-1}f(g),\end{align*} $$
 $z\in \frak h^{{\Sigma _{\infty }}}$
,
$z\in \frak h^{{\Sigma _{\infty }}}$
,  $$ \begin{align*}j_{\underline{w}}({\left(\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\right)}, z_{}) := (ad-bc)^{(w_{0}-w)/2} (cz+d )^{w}.\end{align*} $$
$$ \begin{align*}j_{\underline{w}}({\left(\begin{smallmatrix}a&b\\c&d\end{smallmatrix}\right)}, z_{}) := (ad-bc)^{(w_{0}-w)/2} (cz+d )^{w}.\end{align*} $$
-
(2) There is a Whittaker–Fourier expansion
(2.2.1)for all $$ \begin{align}\begin{aligned} f\left(\left(\begin{array}{cc}y&x\\&1\end{array}\right)\right) &= |y| \sum_{a\in F} W^{\mathbf{C}}_{f,a}(y)(Y) \, {\mathbf{q}}^{a} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} f\left(\left(\begin{array}{cc}y&x\\&1\end{array}\right)\right) &= |y| \sum_{a\in F} W^{\mathbf{C}}_{f,a}(y)(Y) \, {\mathbf{q}}^{a} \end{aligned}\end{align} $$
 $y\in {\mathbf {A}}^{+}$
,
$y\in {\mathbf {A}}^{+}$
,
 $x\in {\mathbf {A}}$
, where:
$x\in {\mathbf {A}}$
, where:
-
• we have
for polynomials $$ \begin{align*}W_{f,0}^{\mathbf{C}}(y)= y_{\infty}^{(w_{0}+w-2)/2} \mathrm{W}_{f, 0}(y) , \quad W_{f,a}^{\mathbf{C}}(y) = (ay_{\infty})^{(w_{0}+w-2)/2} \mathrm{W}_{f, a}(y) \quad (a\neq 0)\end{align*} $$
of degree
$$ \begin{align*}W_{f,0}^{\mathbf{C}}(y)= y_{\infty}^{(w_{0}+w-2)/2} \mathrm{W}_{f, 0}(y) , \quad W_{f,a}^{\mathbf{C}}(y) = (ay_{\infty})^{(w_{0}+w-2)/2} \mathrm{W}_{f, a}(y) \quad (a\neq 0)\end{align*} $$
of degree $$ \begin{align*}\mathrm{W}_{f, a}(y)\in \mathbf{C}[(T_{\tau})_{\tau\in \Sigma_{\infty}}]\end{align*} $$
$$ \begin{align*}\mathrm{W}_{f, a}(y)\in \mathbf{C}[(T_{\tau})_{\tau\in \Sigma_{\infty}}]\end{align*} $$
 $\leq m_{\tau }$
in the variables
$\leq m_{\tau }$
in the variables
 $T_{\tau }$
, evaluated at
$T_{\tau }$
, evaluated at
 $Y:=(Y_{\tau })_{\tau \in \Sigma _{\infty }}$
with
$Y:=(Y_{\tau })_{\tau \in \Sigma _{\infty }}$
with
 $Y_{\tau }= (4\pi y_{\tau })^{-1}$
;
$Y_{\tau }= (4\pi y_{\tau })^{-1}$
;
-
• we denote
 $$ \begin{align*}\mathbf{q}^{a} := \psi(ax) \psi_{\infty}(\mathrm{i} a y_{\infty}).\end{align*} $$
$$ \begin{align*}\mathbf{q}^{a} := \psi(ax) \psi_{\infty}(\mathrm{i} a y_{\infty}).\end{align*} $$
-
The polynomial
![]() $\mathrm {W}_{f,a}(y)$
only depends on the class of
$\mathrm {W}_{f,a}(y)$
only depends on the class of
![]() $ay$
modulo
$ay$
modulo
![]() $\mathbf {a}^{-1}(U)$
, so that defining
$\mathbf {a}^{-1}(U)$
, so that defining
for
![]() $a\in \mathbf {A}^{+}$
, for all
$a\in \mathbf {A}^{+}$
, for all
![]() $a\in F^{+}$
, and for
$a\in F^{+}$
, and for
![]() $y\in \mathbf {A}^{+}$
, we have
$y\in \mathbf {A}^{+}$
, we have
![]() $W_{f,a}(y)=W_{f} (ay)$
. We say that f is cuspidal if
$W_{f,a}(y)=W_{f} (ay)$
. We say that f is cuspidal if
![]() $W_{0}(y)=0$
for all y.
$W_{0}(y)=0$
for all y.
If f is nearly holomorphic of degree
![]() $0$
(that is,
$0$
(that is,
![]() $\leq (0, \ldots , 0)$
), we simply say that f is a (holomorphic) modular form. If
$\leq (0, \ldots , 0)$
), we simply say that f is a (holomorphic) modular form. If
![]() $R\subset \mathbf {C}$
is any subring, we denote by
$R\subset \mathbf {C}$
is any subring, we denote by
respectively, the spaces of cuspidal forms and holomorphic forms of level U and weight
![]() $\underline {w}$
, and of nearly holomorphic forms of level U, weight
$\underline {w}$
, and of nearly holomorphic forms of level U, weight
![]() $\underline {w}$
, and degree
$\underline {w}$
, and degree
![]() $\leq m=(m_{\tau })$
, such that for all
$\leq m=(m_{\tau })$
, such that for all
![]() $a\in \mathbf {A}^{+}$
, the polynomials
$a\in \mathbf {A}^{+}$
, the polynomials
![]() $W_f({a})$
have coefficients in R. We write
$W_f({a})$
have coefficients in R. We write
![]() $N_{\underline {w}}^{}(U, R):= \varinjlim _{m} N_{\underline {w}}^{ \leq m}(U, R)$
, and
$N_{\underline {w}}^{}(U, R):= \varinjlim _{m} N_{\underline {w}}^{ \leq m}(U, R)$
, and
![]() $\Box (R):=\varinjlim _{U} \Box (U, R)$
if
$\Box (R):=\varinjlim _{U} \Box (U, R)$
if
![]() $\Box $
stands for the notation for any of the spaces of forms defined above (or below).
$\Box $
stands for the notation for any of the spaces of forms defined above (or below).
Finally, we define the space
![]() $S^{\mathrm {a}}_{\underline {w}}(U, \mathbf {C})$
of antiholomorphic cuspforms to be the
$S^{\mathrm {a}}_{\underline {w}}(U, \mathbf {C})$
of antiholomorphic cuspforms to be the
![]() $\mathbf {C}$
-vector space image of
$\mathbf {C}$
-vector space image of
![]() $S_{\underline {w}}(U, \mathbf {C})$
under complex conjugation. The formula
$S_{\underline {w}}(U, \mathbf {C})$
under complex conjugation. The formula
 $$ \begin{align}\begin{aligned} f\mapsto f^{\mathrm{a}}:=\left(\begin{array}{cc}-1&\\&1\end{array}\right) f \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} f\mapsto f^{\mathrm{a}}:=\left(\begin{array}{cc}-1&\\&1\end{array}\right) f \end{aligned}\end{align} $$
(where
![]() $\left (\begin {smallmatrix}-1&\\&1\end {smallmatrix}\right ) \in \mathrm {G}(F)\subset \mathrm {G}(\mathbf {A})$
acts, as usual, by right translation) defines
$\left (\begin {smallmatrix}-1&\\&1\end {smallmatrix}\right ) \in \mathrm {G}(F)\subset \mathrm {G}(\mathbf {A})$
acts, as usual, by right translation) defines
![]() $\mathbf {C}$
-linear bijections from
$\mathbf {C}$
-linear bijections from
![]() $S_{\underline {w}}(U, \mathbf {C})$
to
$S_{\underline {w}}(U, \mathbf {C})$
to
![]() $S^{\mathrm {a}}_{\underline {w}}(U, \mathbf {C})$
and vice versa.
$S^{\mathrm {a}}_{\underline {w}}(U, \mathbf {C})$
and vice versa.
2.2.2 Twisted modular forms
A twisted nearly holomorphic (Hilbert) modular form of weight
![]() $\underline {w}$
, level U, and degree
$\underline {w}$
, level U, and degree
![]() $\leq m=(m_{\tau })$
is a function
$\leq m=(m_{\tau })$
is a function
satisfying the following two conditions:
-
(1) For all
 $g\in \mathrm {G}(\mathbf {A})$
,
$g\in \mathrm {G}(\mathbf {A})$
,
 $\gamma \in \mathrm {G}(F)$
, and
$\gamma \in \mathrm {G}(F)$
, and
 $k \in U C_{\infty }^{+}$
,
$k \in U C_{\infty }^{+}$
,  $$ \begin{align*}f(\gamma g k, \det(\gamma)^{-1} u) = j_{\underline{w}}(k_{\infty}, \mathrm{i})^{-1} f(g, u).\end{align*} $$
$$ \begin{align*}f(\gamma g k, \det(\gamma)^{-1} u) = j_{\underline{w}}(k_{\infty}, \mathrm{i})^{-1} f(g, u).\end{align*} $$
-
(2) There is a Whittaker–Fourier expansion
(2.2.4)for all $$ \begin{align}\begin{aligned} f\left(\left(\begin{array}{cc}y&x\\&1\end{array}\right) , u\right) &= |y| \sum_{a\in F} W^{\mathbf{C}}_{f, a}(y, u)(Y) \, {\mathbf{q}}^{a} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} f\left(\left(\begin{array}{cc}y&x\\&1\end{array}\right) , u\right) &= |y| \sum_{a\in F} W^{\mathbf{C}}_{f, a}(y, u)(Y) \, {\mathbf{q}}^{a} \end{aligned}\end{align} $$
 $x\in {\mathbf {A}}$
and
$x\in {\mathbf {A}}$
and
 $y, u\in {\mathbf {A}}^{\times }$
such that
$y, u\in {\mathbf {A}}^{\times }$
such that
 $(uy)_{\infty }>0$
, where:
$(uy)_{\infty }>0$
, where:  $$ \begin{align*} &W_{f, 0}^{\mathbf{C}}(y, u)= y_{\infty}^{(w_{0}+w-2)/2} \mathrm{W}_{f, 0}(y, u) ,\\ & W_{f, a}^{\mathbf{C}}(y, u) = (ay_{\infty})^{(w_{0}+w-2)/2} \mathrm{W}_{f, a}(y, u) \quad (a \neq 0)\end{align*} $$
$$ \begin{align*} &W_{f, 0}^{\mathbf{C}}(y, u)= y_{\infty}^{(w_{0}+w-2)/2} \mathrm{W}_{f, 0}(y, u) ,\\ & W_{f, a}^{\mathbf{C}}(y, u) = (ay_{\infty})^{(w_{0}+w-2)/2} \mathrm{W}_{f, a}(y, u) \quad (a \neq 0)\end{align*} $$
for polynomials
of degree $$ \begin{align*}\mathrm{W}_{f, a}(y, u)\in \mathbf{C}[(T_{\tau})_{\tau\colon F\hookrightarrow \mathbf{R}}]\end{align*} $$
$$ \begin{align*}\mathrm{W}_{f, a}(y, u)\in \mathbf{C}[(T_{\tau})_{\tau\colon F\hookrightarrow \mathbf{R}}]\end{align*} $$
 $\leq m_{\tau }$
in the variables
$\leq m_{\tau }$
in the variables
 $T_{\tau }$
, evaluated at
$T_{\tau }$
, evaluated at
 $Y:=(Y_{\tau })_{\tau \colon F\hookrightarrow \mathbf {R}}$
with
$Y:=(Y_{\tau })_{\tau \colon F\hookrightarrow \mathbf {R}}$
with
 $Y_{\tau }= (4\pi y_{\tau })^{-1}$
.
$Y_{\tau }= (4\pi y_{\tau })^{-1}$
.
If
![]() $R\subset \mathbf {C}$
is any subring, we denote by
$R\subset \mathbf {C}$
is any subring, we denote by
![]() $ M^{\mathrm {tw }}_{\underline {w}}(U, R)\subset N_{\underline {w}}^{\mathrm {tw}, \leq m}(U, R)$
the spaces of holomorphic and nearly holomorphic forms of level U, weight
$ M^{\mathrm {tw }}_{\underline {w}}(U, R)\subset N_{\underline {w}}^{\mathrm {tw}, \leq m}(U, R)$
the spaces of holomorphic and nearly holomorphic forms of level U, weight
![]() $\underline {w}$
, and degree
$\underline {w}$
, and degree
![]() $\leq m=(m_{\tau })$
, such that all the polynomials
$\leq m=(m_{\tau })$
, such that all the polynomials
![]() $\mathrm {W}_{f, a}(y, u)$
have coefficients in R.
$\mathrm {W}_{f, a}(y, u)$
have coefficients in R.
2.2.3 Contracted product
For any open compact subgroup
![]() $U_{F}\subset \widehat {\mathscr {O}}_{F}^{\times }$
, let
$U_{F}\subset \widehat {\mathscr {O}}_{F}^{\times }$
, let
 $$ \begin{align}\begin{aligned} \qquad \mu_{U_{F}}:= F^{\times}\cap U_{F}, \qquad \nu_{U_{F}}:=|\{\pm 1\} \cap \mu_{U_{F}}|, \qquad \qquad c_{U_{F}}= {\nu_{U_{F}} \cdot 2^{[F:\mathbf{Q}]}h_{F}\over [\mathscr{O}_{F}^{\times}:\mu_{U_{F}}^{2}]}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \qquad \mu_{U_{F}}:= F^{\times}\cap U_{F}, \qquad \nu_{U_{F}}:=|\{\pm 1\} \cap \mu_{U_{F}}|, \qquad \qquad c_{U_{F}}= {\nu_{U_{F}} \cdot 2^{[F:\mathbf{Q}]}h_{F}\over [\mathscr{O}_{F}^{\times}:\mu_{U_{F}}^{2}]}. \end{aligned}\end{align} $$
Let
![]() $\varphi \colon \mathbf {A}^{\times }\to \mathbf {C}$
be a Schwartz function, invariant under a subgroup of the form
$\varphi \colon \mathbf {A}^{\times }\to \mathbf {C}$
be a Schwartz function, invariant under a subgroup of the form
![]() $\mu _{U_{F}'}^{2}\subset F^{\times }$
as above. Then the sum
$\mu _{U_{F}'}^{2}\subset F^{\times }$
as above. Then the sum
 $$ \begin{align}\begin{aligned} \sum^{\star}_{u\in F^{\times}} \varphi(u):= c_{U_{F}}\sum_{u\in \mu_{U_{F}}^{2}\backslash F^{\times}} \varphi(u) \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum^{\star}_{u\in F^{\times}} \varphi(u):= c_{U_{F}}\sum_{u\in \mu_{U_{F}}^{2}\backslash F^{\times}} \varphi(u) \end{aligned}\end{align} $$
is well defined independently of
![]() $U_{F}\subset U_{F}'$
, and for any such choice, the support of the sum is finite.
$U_{F}\subset U_{F}'$
, and for any such choice, the support of the sum is finite.
If
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
are twisted nearly holomorphic forms, we may thus define a (plain) nearly holomorphic form
$f_{2}$
are twisted nearly holomorphic forms, we may thus define a (plain) nearly holomorphic form
![]() $f_{1} \star f_{2}$
by
$f_{1} \star f_{2}$
by
 $$ \begin{align}\begin{aligned} f_{1} \star f_{2}(g):= \sum_{u\in F^{\times}}^{\star} f_{1}(g, u)f_{2}(g, u). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} f_{1} \star f_{2}(g):= \sum_{u\in F^{\times}}^{\star} f_{1}(g, u)f_{2}(g, u). \end{aligned}\end{align} $$
2.2.4 Differential operators
We attach to a nearly holomorphic (genuine or twisted) form f the function
 $$ \begin{align*}\begin{aligned} f^{\frak h}\colon \mathrm{G}(\mathbf{A}^{\infty})\times \frak h^{{\Sigma_{\infty}}} &\to \mathbf{C} \\ (g^{\infty}, z=g_{\infty} \mathrm{i})& \mapsto j_{\underline{w}}(g_{\infty}, \mathrm{i}) f(g_{\infty}); \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} f^{\frak h}\colon \mathrm{G}(\mathbf{A}^{\infty})\times \frak h^{{\Sigma_{\infty}}} &\to \mathbf{C} \\ (g^{\infty}, z=g_{\infty} \mathrm{i})& \mapsto j_{\underline{w}}(g_{\infty}, \mathrm{i}) f(g_{\infty}); \end{aligned}\end{align*} $$
the map
![]() $f\mapsto f^{\frak h}$
is injective.
$f\mapsto f^{\frak h}$
is injective.
The Maass–Shimura differential operators on functions on
![]() $\frak h^{{\Sigma _{\infty }}}$
are defined as follows. For
$\frak h^{{\Sigma _{\infty }}}$
are defined as follows. For
![]() $\tau \colon F\hookrightarrow \mathbf {R}$
and
$\tau \colon F\hookrightarrow \mathbf {R}$
and
![]() $w \in \mathbf {Z}$
, let
$w \in \mathbf {Z}$
, let
 $$ \begin{align*}\delta_{w}^{\tau, \frak h}:= {1\over 2\pi i} \left({w\over 2i y_{\tau}}+ {\partial \over \partial z_{\tau}}\right), \qquad d^{\tau}:= {1\over 2\pi i} {\partial\over \partial z_{\tau}},\end{align*} $$
$$ \begin{align*}\delta_{w}^{\tau, \frak h}:= {1\over 2\pi i} \left({w\over 2i y_{\tau}}+ {\partial \over \partial z_{\tau}}\right), \qquad d^{\tau}:= {1\over 2\pi i} {\partial\over \partial z_{\tau}},\end{align*} $$
a differential operator on the upper half-plane
![]() $\frak h$
. For
$\frak h$
. For
![]() $w,k \in \mathbf {Z}_{\geq 0}^{{\Sigma _{\infty }}}$
, let
$w,k \in \mathbf {Z}_{\geq 0}^{{\Sigma _{\infty }}}$
, let
Then, for any ring
![]() $\mathbf {Q}\subset R\subset \mathbf {C}$
, this operator defines a map
$\mathbf {Q}\subset R\subset \mathbf {C}$
, this operator defines a map
such that
![]() $\delta _{w}^{k}(f)^{\frak h}=\delta _{w}^{k, \frak h}(f^{\frak h})$
. (For a proof of the intuitive fact that the archimedean operator
$\delta _{w}^{k}(f)^{\frak h}=\delta _{w}^{k, \frak h}(f^{\frak h})$
. (For a proof of the intuitive fact that the archimedean operator
![]() $\delta _{\underline {w}}^{k}$
indeed preserves the rationality properties of finite Whittaker–Fourier coefficients, see [Reference HidaHid91, Proposition 1.2], whose calculations also apply to the twisted case.) The subscript w will be omitted if it is clear from the context.
$\delta _{\underline {w}}^{k}$
indeed preserves the rationality properties of finite Whittaker–Fourier coefficients, see [Reference HidaHid91, Proposition 1.2], whose calculations also apply to the twisted case.) The subscript w will be omitted if it is clear from the context.
By [Reference ShimuraShi81, equation (1.16)], for all
![]() $k\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
, we have
$k\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
, we have
 $$ \begin{align}\begin{aligned} \delta_{w}^{k}=\sum_{0 \leq j\leq k} \prod_{\tau\in \Sigma_{\infty}} {k_{\tau}\choose j_{\tau}} {\Gamma(w_{\tau}+k_{\tau})\over \Gamma(w_{\tau}+j_{\tau})} (-4\pi y_{\tau})^{j_{\tau}-k_{\tau}} \, d^{j_{}}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \delta_{w}^{k}=\sum_{0 \leq j\leq k} \prod_{\tau\in \Sigma_{\infty}} {k_{\tau}\choose j_{\tau}} {\Gamma(w_{\tau}+k_{\tau})\over \Gamma(w_{\tau}+j_{\tau})} (-4\pi y_{\tau})^{j_{\tau}-k_{\tau}} \, d^{j_{}}. \end{aligned}\end{align} $$
If
![]() $w\geq 2m+1$
, any
$w\geq 2m+1$
, any
![]() $f\in N_{\underline {w}}^{\mathrm {(tw), \leq m}}(U, R)$
can be written uniquely as
$f\in N_{\underline {w}}^{\mathrm {(tw), \leq m}}(U, R)$
can be written uniquely as
with
![]() $f_{r}\in M_{\underline {w}+(0; -2r)}^{\mathrm {(tw) }}(U, R)$
. (The proof in [Reference ShimuraShi76, Lemma 7] carries over to our context.) Thus, the linear map
$f_{r}\in M_{\underline {w}+(0; -2r)}^{\mathrm {(tw) }}(U, R)$
. (The proof in [Reference ShimuraShi76, Lemma 7] carries over to our context.) Thus, the linear map
 $$ \begin{align}\begin{aligned} e^{\mathrm{hol}}\colon N_{\underline{w}}^{\mathrm{(tw), \leq m}}(U, R) &\to M_{\underline{w}}^{\mathrm{(tw)}}(U, R)\\ f&\mapsto f_{0}\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} e^{\mathrm{hol}}\colon N_{\underline{w}}^{\mathrm{(tw), \leq m}}(U, R) &\to M_{\underline{w}}^{\mathrm{(tw)}}(U, R)\\ f&\mapsto f_{0}\end{aligned}\end{align} $$
is well defined.
2.3 p-adic modular forms
We study the completions of spaces of modular forms for certain p-adic norms.
2.3.1 Arithmetic q-expansion
Let
![]() $\underline {w}$
be a weight for
$\underline {w}$
be a weight for
![]() $\mathrm {G}$
, and let
$\mathrm {G}$
, and let
![]() $U\subset \mathrm {G}(\mathbf {A}^{\infty })$
be a compact open subgroup. The q-expansion map
$U\subset \mathrm {G}(\mathbf {A}^{\infty })$
be a compact open subgroup. The q-expansion map
sends
![]() $S_{\underline {w}}(U,\mathbf {C})$
to
$S_{\underline {w}}(U,\mathbf {C})$
to
![]() $ \mathbf {C}^{\mathbf {A}^{+}/U_{F}F_{\infty }^{+}}$
, where
$ \mathbf {C}^{\mathbf {A}^{+}/U_{F}F_{\infty }^{+}}$
, where
![]() $U_{F}=\mathbf {a}^{-1}(U)$
. By the q-expansion principle (see [Reference DisegniDis17, Proposition 2.1.1] for a version in our setting), the map is injective. We denote its image by
$U_{F}=\mathbf {a}^{-1}(U)$
. By the q-expansion principle (see [Reference DisegniDis17, Proposition 2.1.1] for a version in our setting), the map is injective. We denote its image by
![]() $\mathrm {S}_{\underline {w}}(U,\mathbf {C})$
and view the map
$\mathrm {S}_{\underline {w}}(U,\mathbf {C})$
and view the map
![]() $S_{\underline {w}}(U,\mathbf {C})\to \mathrm { S}_{\underline {w}}(U,\mathbf {C})$
as an identification.
$S_{\underline {w}}(U,\mathbf {C})\to \mathrm { S}_{\underline {w}}(U,\mathbf {C})$
as an identification.
If R is any ring admitting embeddings into
![]() $\mathbf {C}$
, we denote by
$\mathbf {C}$
, we denote by
the set of those sequences
such that for any
![]() $\iota \colon R\hookrightarrow \mathbf {C}$
, the sequence
$\iota \colon R\hookrightarrow \mathbf {C}$
, the sequence
![]() $\mathrm {f}^{\iota }:=(\iota \mathrm {W}_{\mathrm {f}}(a))_{a}$
is the q-expansion of a cuspform
$\mathrm {f}^{\iota }:=(\iota \mathrm {W}_{\mathrm {f}}(a))_{a}$
is the q-expansion of a cuspform
(In (2.3.1), the notation
![]() $\mathrm {W}_{\mathrm {f}}$
can be thought of as simply synonymous to
$\mathrm {W}_{\mathrm {f}}$
can be thought of as simply synonymous to
![]() $\mathrm {f}$
; it is introduced in order to match the identification of the previous paragraph.) By [Reference HidaHid91, Theorem 2.2(i)] (together with a consideration of Galois actions mixing the weights), for any such ring R, we have
$\mathrm {f}$
; it is introduced in order to match the identification of the previous paragraph.) By [Reference HidaHid91, Theorem 2.2(i)] (together with a consideration of Galois actions mixing the weights), for any such ring R, we have
![]() $\mathrm {S}_{\bullet }(U, R)= \mathrm {S}_{\bullet }(U, \mathbf {Z})\otimes R$
. For more general rings, the previous equality is taken to be the definition of
$\mathrm {S}_{\bullet }(U, R)= \mathrm {S}_{\bullet }(U, \mathbf {Z})\otimes R$
. For more general rings, the previous equality is taken to be the definition of
![]() $\mathrm {S}_{\bullet }(U, R)$
.
$\mathrm {S}_{\bullet }(U, R)$
.
2.3.2 p-adic modular forms
Let L be a finite extension of
![]() $\mathbf {Q}_{p}$
splitting F. A p-adic L-valued (cohomological) weight
$\mathbf {Q}_{p}$
splitting F. A p-adic L-valued (cohomological) weight
![]() $\underline {w}=(w_{0}, (w_{\tau })_{\tau \colon F\hookrightarrow L})$
is a tuple of integers, all having the same parity, such that
$\underline {w}=(w_{0}, (w_{\tau })_{\tau \colon F\hookrightarrow L})$
is a tuple of integers, all having the same parity, such that
![]() $w_{\tau }\geq 1$
for all
$w_{\tau }\geq 1$
for all
![]() $\tau \colon F\hookrightarrow L$
. As in Section 1.1.1, if
$\tau \colon F\hookrightarrow L$
. As in Section 1.1.1, if
![]() $\underline {w}$
is an L-valued weight and
$\underline {w}$
is an L-valued weight and
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
is an embedding, we define the complex weight
$\iota \colon L\hookrightarrow \mathbf {C}$
is an embedding, we define the complex weight
![]() $\underline {w}^{\iota }=(w_{0}, (w_{\tau })_{\iota \circ \tau })$
.
$\underline {w}^{\iota }=(w_{0}, (w_{\tau })_{\iota \circ \tau })$
.
Let
![]() $U\subset \mathrm {G}(\mathbf {A}^{\infty })$
be a compact open subgroup, and let
$U\subset \mathrm {G}(\mathbf {A}^{\infty })$
be a compact open subgroup, and let
![]() $\underline {w} $
be an L-valued weight. We define
$\underline {w} $
be an L-valued weight. We define
![]() $\mathrm { S}_{\underline {w}}(U, L)$
to be the set of q-expansions
$\mathrm { S}_{\underline {w}}(U, L)$
to be the set of q-expansions
![]() $\mathrm {f}$
such that for every
$\mathrm {f}$
such that for every
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, the expansion
$\iota \colon L\hookrightarrow \mathbf {C}$
, the expansion
![]() $\mathrm {f}^{\iota }$
belongs to
$\mathrm {f}^{\iota }$
belongs to
![]() $\mathrm {S}_{\underline {w}^{\iota }}(U,\mathbf {C})$
. The p-adic q-expansion of
$\mathrm {S}_{\underline {w}^{\iota }}(U,\mathbf {C})$
. The p-adic q-expansion of
![]() $\mathrm {f}=(\mathrm {W}_{\mathrm {f}}({a}))_{a}\in \mathrm {S}_{\underline {w}}(U, L)$
is the sequence
$\mathrm {f}=(\mathrm {W}_{\mathrm {f}}({a}))_{a}\in \mathrm {S}_{\underline {w}}(U, L)$
is the sequence
so that
is the Whittaker–Fourier coefficient of
![]() $f^{\iota }$
as in (2.2.1). (In other words, we have two embeddings
$f^{\iota }$
as in (2.2.1). (In other words, we have two embeddings
![]() $\mathrm {S}_{\underline {w}}(U, L)\hookrightarrow L^{\mathbf {A}^{+}/U_{F}F_{\infty }^{+}}$
: the q-expansion
$\mathrm {S}_{\underline {w}}(U, L)\hookrightarrow L^{\mathbf {A}^{+}/U_{F}F_{\infty }^{+}}$
: the q-expansion
![]() $\mathrm {f} \mapsto (\mathrm {W}_{\mathrm {f}}(a))_{a}$
, and the p-adic q-expansion
$\mathrm {f} \mapsto (\mathrm {W}_{\mathrm {f}}(a))_{a}$
, and the p-adic q-expansion
![]() $\mathrm {f}\mapsto (W_{\mathrm {f}}(a))_{a}$
.)
$\mathrm {f}\mapsto (W_{\mathrm {f}}(a))_{a}$
.)
Let
![]() $U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
be a compact open subgroups, let
$U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
be a compact open subgroups, let
![]() $U_{F}^{p}:=\mathbf {a}^{-1}(U^{p})$
, and for any L-valued weight
$U_{F}^{p}:=\mathbf {a}^{-1}(U^{p})$
, and for any L-valued weight
![]() $\underline {w}$
, we denote
$\underline {w}$
, we denote
The space of cuspidal p-adic modular forms
is the completion of
![]() $\mathrm {S}_{\underline {w}}(U^{p}, L)$
for the norm
$\mathrm {S}_{\underline {w}}(U^{p}, L)$
for the norm
![]() $||\mathrm {f}||:= \sup _{a} |W_{\mathrm {f}}(a)|$
, for any
$||\mathrm {f}||:= \sup _{a} |W_{\mathrm {f}}(a)|$
, for any
![]() $\underline {w}$
. By a fundamental result of Hida (see [Reference HidaHid91, paragraph after Theorem 3.1]), the space
$\underline {w}$
. By a fundamental result of Hida (see [Reference HidaHid91, paragraph after Theorem 3.1]), the space
![]() $\mathbf {S}(U^{p}, L)$
is independent of the choice of
$\mathbf {S}(U^{p}, L)$
is independent of the choice of
![]() $\underline {w}$
. In particular, if L is Galois over
$\underline {w}$
. In particular, if L is Galois over
![]() $\mathbf {Q}_{p}$
, this space is stable by the action of
$\mathbf {Q}_{p}$
, this space is stable by the action of
![]() $\mathrm {Gal}(L/\mathbf {Q}_{p})$
and so it is of the form
$\mathrm {Gal}(L/\mathbf {Q}_{p})$
and so it is of the form
![]() $\mathbf {S}(U^{p}, \mathbf {Q}_{p})\otimes _{\mathbf {Q}_{p}}L$
for a space
$\mathbf {S}(U^{p}, \mathbf {Q}_{p})\otimes _{\mathbf {Q}_{p}}L$
for a space
![]() $\mathbf { S}(U^{p}, \mathbf {Q}_{p})$
.
$\mathbf { S}(U^{p}, \mathbf {Q}_{p})$
.
2.3.3 Nearly holomorphic forms as p-adic modular forms
We may attach a p-adic q-expansion to a nearly holomorphic form with coefficients in a p-adic subfield of
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
Let L be a finite extension of
![]() $\mathbf {Q}_{p}$
, and let
$\mathbf {Q}_{p}$
, and let
![]() $\underline {w}$
be a p-adic L-valued weight. We say that
$\underline {w}$
be a p-adic L-valued weight. We say that
is a p-adic nearly holomorphic cuspform of weight
![]() $\underline {w}$
and level
$\underline {w}$
and level
![]() $U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
if the following condition holds. For each
$U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
if the following condition holds. For each
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, there exists a cuspidal nearly holomorphic form
$\iota \colon L\hookrightarrow \mathbf {C}$
, there exists a cuspidal nearly holomorphic form
for some
![]() $n\in \mathbf {Z}_{\geq 1}^{S_{p}}$
, whose Whittaker–Fourier polynomials have constant terms satisfying
$n\in \mathbf {Z}_{\geq 1}^{S_{p}}$
, whose Whittaker–Fourier polynomials have constant terms satisfying
The notion of a p-adic twisted nearly holomorphic cuspform is defined similarly by the identity
![]() $\mathrm {W}_{f^{\iota }, a}(y, u)(0) = \iota \left ((ay)_{p}^{(-w_{0}-w+2)/2}W_{f}(a)(y, u)\right )$
.
$\mathrm {W}_{f^{\iota }, a}(y, u)(0) = \iota \left ((ay)_{p}^{(-w_{0}-w+2)/2}W_{f}(a)(y, u)\right )$
.
Proposition 2.2 If f is a p-adic nearly holomorphic cuspform over L of level
![]() $U^{p}$
, then it belongs to the space
$U^{p}$
, then it belongs to the space
![]() $\mathbf {S}(U^{p},L)$
of p-adic modular cuspforms of level
$\mathbf {S}(U^{p},L)$
of p-adic modular cuspforms of level
![]() $U^{p}$
.
$U^{p}$
.
Proof This is the first assertion of [Reference HidaHid91, Proposition 7.3].
2.3.4 Hecke operators and ordinary projection
The space
![]() $N_{\underline {w}}(U, \mathbf {C})$
is endowed with the usual action of
$N_{\underline {w}}(U, \mathbf {C})$
is endowed with the usual action of
![]() $\mathscr {H}_{U}$
. By writing down the effect of this action on Whittaker–Fourier coefficients of cuspforms, we may descend it to a bounded action of
$\mathscr {H}_{U}$
. By writing down the effect of this action on Whittaker–Fourier coefficients of cuspforms, we may descend it to a bounded action of
![]() $\mathscr {H}_{U^{p}, L}$
on
$\mathscr {H}_{U^{p}, L}$
on
![]() $\mathrm { S}_{\underline {w}}(U^{p},L)$
, and hence on
$\mathrm { S}_{\underline {w}}(U^{p},L)$
, and hence on
![]() $\mathbf {S}(U^{p}, L)$
, for any p-adic field L.
$\mathbf {S}(U^{p}, L)$
, for any p-adic field L.
For
![]() $t\in A_{p}^{+}$
or
$t\in A_{p}^{+}$
or
![]() $y\in \prod _{v\vert {p}}\mathscr {O}_{F, v}-\{0\}$
, and any
$y\in \prod _{v\vert {p}}\mathscr {O}_{F, v}-\{0\}$
, and any
![]() $n\in \mathbf {Z}_{\geq 1} ^{S_{p}}$
, define the double coset operators
$n\in \mathbf {Z}_{\geq 1} ^{S_{p}}$
, define the double coset operators
 $$ \begin{align}\begin{aligned} \mathrm{U}_{t}&:=[U_{p, n} \, t \, U_{p, n}], \qquad &\mathrm{U}_{t}^{\circ, \underline{w}} := t_{1}^{2-w}\det(t)^{(-w_{0}+w-2)/2} \mathrm{U}_{t}, \\ \mathrm{U}_{y}&:= \mathrm{U}_{\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right)},\qquad & \mathrm{U}_{y}^{\circ, \underline{w}}:= y^{(-w_{0}-w+2)/2 } \mathrm{U}_{y}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathrm{U}_{t}&:=[U_{p, n} \, t \, U_{p, n}], \qquad &\mathrm{U}_{t}^{\circ, \underline{w}} := t_{1}^{2-w}\det(t)^{(-w_{0}+w-2)/2} \mathrm{U}_{t}, \\ \mathrm{U}_{y}&:= \mathrm{U}_{\left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right)},\qquad & \mathrm{U}_{y}^{\circ, \underline{w}}:= y^{(-w_{0}-w+2)/2 } \mathrm{U}_{y}. \end{aligned}\end{align} $$
If L is a finite extension of
![]() $\mathbf {Q}_{p}$
, then for all
$\mathbf {Q}_{p}$
, then for all
![]() $y\in \prod _{v\vert p}\mathscr {O}_{F, v}-\{0\}$
, we also define the operator
$y\in \prod _{v\vert p}\mathscr {O}_{F, v}-\{0\}$
, we also define the operator
 $$ \begin{align*}\begin{aligned} \mathrm{U}_{y}^{\circ}\colon \mathbf{S}(U^{p}, L) &\to \mathbf{S}(U^{p}, L)\\ W_{\mathrm{U}_{y}^{\circ}f}(c)&:= W_{f}(cy).\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \mathrm{U}_{y}^{\circ}\colon \mathbf{S}(U^{p}, L) &\to \mathbf{S}(U^{p}, L)\\ W_{\mathrm{U}_{y}^{\circ}f}(c)&:= W_{f}(cy).\end{aligned}\end{align*} $$
This is compatible with the previous definition in the following sense (see [Reference HidaHid91, equation (2.2b)], where
![]() $\mathrm {U}_{y}$
is denoted by
$\mathrm {U}_{y}$
is denoted by
![]() $T(y)$
): if f is a p-adic nearly holomorphic form of weight
$T(y)$
): if f is a p-adic nearly holomorphic form of weight
![]() $\underline {w}$
over L, then for all
$\underline {w}$
over L, then for all
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, we have
$\iota \colon L\hookrightarrow \mathbf {C}$
, we have
The superscript
![]() $\underline {w}$
will be omitted when understood from the context. The ordinary projector is
$\underline {w}$
will be omitted when understood from the context. The ordinary projector is
for any tame level
![]() $U^{p}$
and p-adic field L. Its image is denoted by
$U^{p}$
and p-adic field L. Its image is denoted by
The operator
![]() $e^{\mathrm {ord}}$
preserves
$e^{\mathrm {ord}}$
preserves
![]() $\mathrm {S}_{\underline {w}}(U^{p},L)$
, and we denote
$\mathrm {S}_{\underline {w}}(U^{p},L)$
, and we denote
![]() $\mathrm {S}^{\mathrm {ord}}_{\underline {w}}(U^{p}, L):= e^{\mathrm {ord}} \mathbf {S}(U^{p},L)$
and
$\mathrm {S}^{\mathrm {ord}}_{\underline {w}}(U^{p}, L):= e^{\mathrm {ord}} \mathbf {S}(U^{p},L)$
and
![]() $\mathrm {S}^{\mathrm {ord}}(U^{p}, L):= \bigoplus _{\underline {w}} \mathrm { S}^{\mathrm {ord}}_{\underline {w}}(U^{p}, L)$
.
$\mathrm {S}^{\mathrm {ord}}(U^{p}, L):= \bigoplus _{\underline {w}} \mathrm { S}^{\mathrm {ord}}_{\underline {w}}(U^{p}, L)$
.
If
![]() $f^{\mathbf {C}}$
is a complex modular form arising as
$f^{\mathbf {C}}$
is a complex modular form arising as
![]() $f^{\mathbf {C}}=f^{\iota }$
for a form
$f^{\mathbf {C}}=f^{\iota }$
for a form
![]() $f\in \mathrm {S}(L)$
for some finite extension L of
$f\in \mathrm {S}(L)$
for some finite extension L of
![]() $\mathbf {Q}_{p}$
and some
$\mathbf {Q}_{p}$
and some
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, we define
$\iota \colon L\hookrightarrow \mathbf {C}$
, we define
2.3.5 Differential operators after ordinary and holomorphic projections
Let L be a finite extension of
![]() $\mathbf {Q}_{p}$
, and let
$\mathbf {Q}_{p}$
, and let
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
be p-adic twisted nearly holomorphic forms over L. For any
$f_{2}$
be p-adic twisted nearly holomorphic forms over L. For any
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
and
$\iota \colon L\hookrightarrow \mathbf {C}$
and
![]() $k \in \mathbf {Z}_{\geq 0}^{{\Sigma _{\infty }}}$
, we have
$k \in \mathbf {Z}_{\geq 0}^{{\Sigma _{\infty }}}$
, we have
the proof of [Reference HidaHid91, Proposition 7.3] carries over to the twisted case.
2.4 Hida families
We gather the fundamental notions concerning Hida families and the associated sheaves of modular forms.
2.4.1 Weight space
Let
![]() $U_{F, p}^{\circ }=\prod _{v\vert p} U_{F, v}^{\circ }\subset \mathscr {O}_{F, p}^{\times }$
be a compact open subgroup (which will be fixed once and for all in Section 2.4.5). Let
$U_{F, p}^{\circ }=\prod _{v\vert p} U_{F, v}^{\circ }\subset \mathscr {O}_{F, p}^{\times }$
be a compact open subgroup (which will be fixed once and for all in Section 2.4.5). Let
![]() $U_{F}^{p}\subset \mathbf {A}^{p\infty , \times }$
be a compact open subgroup, and consider the topological groups (with the profinite topology)
$U_{F}^{p}\subset \mathbf {A}^{p\infty , \times }$
be a compact open subgroup, and consider the topological groups (with the profinite topology)
the latter is isomorphic to
![]() $\Delta \times \mathbf {Z}_{p}^{1+[F:\mathbf {Q}]+\delta _{F,p}}$
, where
$\Delta \times \mathbf {Z}_{p}^{1+[F:\mathbf {Q}]+\delta _{F,p}}$
, where
![]() $\Delta $
is a finite group and
$\Delta $
is a finite group and
![]() $\delta _{F, p}$
is the p-Leopoldt defect of F. It is embedded into
$\delta _{F, p}$
is the p-Leopoldt defect of F. It is embedded into
![]() $A(\mathbf {A}^{\infty })$
by
$A(\mathbf {A}^{\infty })$
by
 $$ \begin{align*}(z, y_{p})\mapsto \left(\begin{array}{cc}zy_{p}&\\&z\end{array}\right).\end{align*} $$
$$ \begin{align*}(z, y_{p})\mapsto \left(\begin{array}{cc}zy_{p}&\\&z\end{array}\right).\end{align*} $$
The weight space (of tame level
![]() $U_{F}^{p}$
) is
$U_{F}^{p}$
) is
A point
![]() $\underline {\kappa }\in \frak W$
is identified with the pair of characters
$\underline {\kappa }\in \frak W$
is identified with the pair of characters
We have an involution defined as
If
![]() $\underline {k}$
is a p-adic weight for
$\underline {k}$
is a p-adic weight for
![]() $\mathrm {G}$
, we say that
$\mathrm {G}$
, we say that
![]() $\underline {\kappa } $
is classical of weight
$\underline {\kappa } $
is classical of weight
![]() $\underline {k}$
if for all
$\underline {k}$
if for all
![]() $v\vert p$
,
$v\vert p$
,
are smooth characters of
![]() $F_{p}^{\times }$
(respectively,
$F_{p}^{\times }$
(respectively,
![]() $U_{F, v}^{\circ }$
); in the second equation,
$U_{F, v}^{\circ }$
); in the second equation,
![]() $\kappa _{v}:=\kappa _{|U^{\circ }_{F,v}}$
, and the product runs over the
$\kappa _{v}:=\kappa _{|U^{\circ }_{F,v}}$
, and the product runs over the
![]() $\tau \in \Sigma _{p}$
inducing the place
$\tau \in \Sigma _{p}$
inducing the place
![]() $v\in S_{p}$
. For a classical weight
$v\in S_{p}$
. For a classical weight
![]() $\underline {\kappa }$
, we define
$\underline {\kappa }$
, we define
![]() $\kappa ^{\mathrm {sm}}:=\otimes _{v\vert p} \kappa _{v}^{\mathrm {sm}}$
and
$\kappa ^{\mathrm {sm}}:=\otimes _{v\vert p} \kappa _{v}^{\mathrm {sm}}$
and
a smooth character of
![]() $U_{F, p}^{\circ }$
.
$U_{F, p}^{\circ }$
.
We denote by
the set of points of classical weight, which has the structure of an ind-étale ind-finite scheme over
![]() $\mathbf {Q}_{p}$
. If
$\mathbf {Q}_{p}$
. If
![]() $\underline {\kappa }$
is classical of weight
$\underline {\kappa }$
is classical of weight
![]() $\underline {k}=(k_{0}, k)$
, then
$\underline {k}=(k_{0}, k)$
, then
![]() $\underline {\kappa }^{\curlyvee }$
is classical of weight
$\underline {\kappa }^{\curlyvee }$
is classical of weight
![]() $\underline {k}^{\vee }=(-k_{0}, k)$
. We let
$\underline {k}^{\vee }=(-k_{0}, k)$
. We let
![]() $\frak W^{\mathrm {cl}, \geq 2}$
be the set of classical points satisfying
$\frak W^{\mathrm {cl}, \geq 2}$
be the set of classical points satisfying
![]() $k \geq 2$
.
$k \geq 2$
.
2.4.2 Hida schemes
In light of the examples of the previous and following paragraphs, it will be convenient to introduce a suitable category of spaces.Footnote
8
Define the category of Hida rings to consist of finite flat
![]() -algebras
-algebras
![]() $A^{\circ }$
(for some n) and
$A^{\circ }$
(for some n) and
![]() $\mathbf {Z}_{p}$
-algebra morphisms, and the category of Hida algebras to be the image of Hida rings under the functor
$\mathbf {Z}_{p}$
-algebra morphisms, and the category of Hida algebras to be the image of Hida rings under the functor
![]() $\otimes _{\mathbf {Z}_{p}}\mathbf {Q}_{p}$
. Define the category of affine Hida schemes to be dual to the category of Hida algebras. A Hida scheme is an open subset of an affine Hida scheme. If
$\otimes _{\mathbf {Z}_{p}}\mathbf {Q}_{p}$
. Define the category of affine Hida schemes to be dual to the category of Hida algebras. A Hida scheme is an open subset of an affine Hida scheme. If
![]() $A_{i}^{\circ }$
are Hida rings (for
$A_{i}^{\circ }$
are Hida rings (for
![]() $i=1, 2$
) and
$i=1, 2$
) and
![]() $\mathscr {X}_{i}=\mathrm {Spec}\, (A_{i}^{\circ }\otimes _{\mathbf {Z}_{p}} \mathbf {Q}_{p})$
(for
$\mathscr {X}_{i}=\mathrm {Spec}\, (A_{i}^{\circ }\otimes _{\mathbf {Z}_{p}} \mathbf {Q}_{p})$
(for
![]() $i=1,2$
), we define
$i=1,2$
), we define
where
![]() $\hat {\otimes }$
is the completed tensor product.
$\hat {\otimes }$
is the completed tensor product.
2.4.3 Hida families
Let
be the images of the Hecke algebras
![]() $\mathscr {H}_{U^{p}, \mathbf {Q}_{p}}^{\mathrm {sph,\ \mathrm {ord}}}$
,
$\mathscr {H}_{U^{p}, \mathbf {Q}_{p}}^{\mathrm {sph,\ \mathrm {ord}}}$
,
![]() $\mathscr {H}_{U^{p}, \mathbf {Q}_{p}}^{\mathrm {ord}}$
from Section 2.1.3. We let
$\mathscr {H}_{U^{p}, \mathbf {Q}_{p}}^{\mathrm {ord}}$
from Section 2.1.3. We let
be the ordinary eigenvariety for
![]() $\mathrm {G}$
of tame level
$\mathrm {G}$
of tame level
![]() $U^{p}$
. (The subscript
$U^{p}$
. (The subscript
![]() $U^{p}$
will be omitted when unimportant or understood from the context.) The space
$U^{p}$
will be omitted when unimportant or understood from the context.) The space
![]() $\mathscr {Y}_{\mathrm {G}, U^{p}}$
is a union of finitely many irreducible components, called Hida families of tame level (dividing)
$\mathscr {Y}_{\mathrm {G}, U^{p}}$
is a union of finitely many irreducible components, called Hida families of tame level (dividing)
![]() $U^{p}$
. It carries an involution
$U^{p}$
. It carries an involution
![]() $\curlyvee $
deduced from the one on
$\curlyvee $
deduced from the one on
![]() $\mathscr {H}_{U^{p}, \mathbf {Q}_{p}}^{\mathrm {sph,\ \mathrm {ord}}}$
.
$\mathscr {H}_{U^{p}, \mathbf {Q}_{p}}^{\mathrm {sph,\ \mathrm {ord}}}$
.
Letting
![]() $U_{F} ^{p}:= U^{p}\cap Z(\mathbf {A}^{p\infty })$
, we have a weight-character map
$U_{F} ^{p}:= U^{p}\cap Z(\mathbf {A}^{p\infty })$
, we have a weight-character map
that, when identified with a pair
![]() $(\kappa _{\mathrm {G}, 0}, \kappa _{\mathrm {G}}) $
of
$(\kappa _{\mathrm {G}, 0}, \kappa _{\mathrm {G}}) $
of
![]() $\mathscr {O}(\mathscr {Y}_{\mathrm {G}})^{\times }$
-valued characters as in (2.4.2), is
$\mathscr {O}(\mathscr {Y}_{\mathrm {G}})^{\times }$
-valued characters as in (2.4.2), is
![]() $\kappa _{\mathrm {G}, 0}(z)=$
the Hecke operator acting by right translation by z on modular forms,
$\kappa _{\mathrm {G}, 0}(z)=$
the Hecke operator acting by right translation by z on modular forms,
![]() $\kappa _{G}(y_{p})= \mathrm {U}_{y_{p}}^{\circ }$
. The weight map is finite and flat, and it intertwines the involutions
$\kappa _{G}(y_{p})= \mathrm {U}_{y_{p}}^{\circ }$
. The weight map is finite and flat, and it intertwines the involutions
![]() $\curlyvee $
.
$\curlyvee $
.
The set of classical points of
![]() $\mathscr {Y}_{\mathrm {G}} $
is
$\mathscr {Y}_{\mathrm {G}} $
is
If
![]() $x_{0}\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}$
, we denote by
$x_{0}\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}$
, we denote by
![]() $\pi _{x_{0}}$
the automorphic representation of
$\pi _{x_{0}}$
the automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
over
$\mathrm {G}(\mathbf {A})$
over
![]() $\mathbf {Q}_{p}(x_{0})$
on which
$\mathbf {Q}_{p}(x_{0})$
on which
![]() $\mathscr {H}^{\mathrm {sph}}_{U^{p}}$
acts by the
$\mathscr {H}^{\mathrm {sph}}_{U^{p}}$
acts by the
![]() $\mathbf {Q}_{p}(x_{0})$
-character corresponding to
$\mathbf {Q}_{p}(x_{0})$
-character corresponding to
![]() $x_{0}$
. If
$x_{0}$
. If
![]() $x\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C})$
corresponds to
$x\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C})$
corresponds to
![]() $(x_{0}\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}, \iota \colon \mathbf {Q}_{p}(x_{0})\hookrightarrow \mathbf {C})$
, we denote
$(x_{0}\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}, \iota \colon \mathbf {Q}_{p}(x_{0})\hookrightarrow \mathbf {C})$
, we denote
![]() $\pi _{x}:= \pi _{x_{0}}^{\iota }$
.
$\pi _{x}:= \pi _{x_{0}}^{\iota }$
.
2.4.4 Families of ordinary forms
By construction, for each
![]() $U^{p}{}'\subset U^{p}$
, the ordinary eigenvariety
$U^{p}{}'\subset U^{p}$
, the ordinary eigenvariety
![]() $\mathscr {Y}_{\mathrm {G}, U^{p}}$
(respectively, the weight space
$\mathscr {Y}_{\mathrm {G}, U^{p}}$
(respectively, the weight space
![]() $\frak W_{U_{F}^{p}}$
) carries a (coherent) sheaf
$\frak W_{U_{F}^{p}}$
) carries a (coherent) sheaf
(respectively,
![]() $\mathscr {S}^{U^{p}{}'}_{\frak W}:=\kappa _{\mathrm {G}, *} \mathscr {S}^{U^{p}{}'}$
), whose modules of global sections are
$\mathscr {S}^{U^{p}{}'}_{\frak W}:=\kappa _{\mathrm {G}, *} \mathscr {S}^{U^{p}{}'}$
), whose modules of global sections are
![]() $\mathbf {S}^{\mathrm {ord}}(U^{p}{}', \mathbf {Q}_{p})$
. We set
$\mathbf {S}^{\mathrm {ord}}(U^{p}{}', \mathbf {Q}_{p})$
. We set
![]() $\mathscr {S}_{(\frak W)}:=\varinjlim _{U^{p}{}'}\mathscr {S}_{(\frak W)}^{U^{p}}.$
By Hida’s Control Theorem (see [Reference HidaHid91, Corollary 3.3]), the restriction of
$\mathscr {S}_{(\frak W)}:=\varinjlim _{U^{p}{}'}\mathscr {S}_{(\frak W)}^{U^{p}}.$
By Hida’s Control Theorem (see [Reference HidaHid91, Corollary 3.3]), the restriction of
![]() $\mathscr {S}_{\frak W}^{U^{p}}$
to
$\mathscr {S}_{\frak W}^{U^{p}}$
to
![]() $\frak W^{\mathrm {cl}}$
is the sheaf attached to
$\frak W^{\mathrm {cl}}$
is the sheaf attached to
![]() $\mathrm {S}^{\mathrm {ord}}(U^{p}, \mathbf {Q}_{p})$
.
$\mathrm {S}^{\mathrm {ord}}(U^{p}, \mathbf {Q}_{p})$
.
For each
![]() $x\in \mathscr {Y}_{\mathrm {G}, U^{p}}^{\mathrm {cl}}$
of weight
$x\in \mathscr {Y}_{\mathrm {G}, U^{p}}^{\mathrm {cl}}$
of weight
![]() $\underline {w}$
, there exists a unique (up to isomorphism) ordinary automorphic representation
$\underline {w}$
, there exists a unique (up to isomorphism) ordinary automorphic representation
![]() $\pi _{x}$
of
$\pi _{x}$
of
![]() $\mathrm {G}(A)$
over
$\mathrm {G}(A)$
over
![]() $L:=\mathbf {Q}_{p}(x)$
of weight
$L:=\mathbf {Q}_{p}(x)$
of weight
![]() $\underline {w}$
such that there is an
$\underline {w}$
such that there is an
![]() $\mathscr {H}_{U^{p}, L}^{\mathrm {ord}}$
-isomorphism
$\mathscr {H}_{U^{p}, L}^{\mathrm {ord}}$
-isomorphism
the isomorphism is unique up to scalars. This defines a bijection between
![]() $\mathscr {Y}_{\mathrm {G}, U^{p}}^{\mathrm {cl}}(\overline {\mathbf {Q}}_{p})$
and the set of isomorphism classes of ordinary automorphic representation
$\mathscr {Y}_{\mathrm {G}, U^{p}}^{\mathrm {cl}}(\overline {\mathbf {Q}}_{p})$
and the set of isomorphism classes of ordinary automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {G}(\mathbf {A})$
over
$\mathrm {G}(\mathbf {A})$
over
![]() $\overline {\mathbf {Q}}_{p}$
with
$\overline {\mathbf {Q}}_{p}$
with
![]() $\pi ^{U^{p}}\neq 0$
.
$\pi ^{U^{p}}\neq 0$
.
Lemma 2.3 Let
![]() $U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty }) $
be a compact open subgroup, and let
$U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty }) $
be a compact open subgroup, and let
![]() $U_{F}^{p}:= U^{p}\cap Z(\mathbf {A}^{p\infty })$
. Let
$U_{F}^{p}:= U^{p}\cap Z(\mathbf {A}^{p\infty })$
. Let
![]() $\mathscr {Z}$
be a Hida scheme endowed with a map
$\mathscr {Z}$
be a Hida scheme endowed with a map
![]() $\varphi \colon \mathscr {Z}\to \frak {W=\frak W}_{U^{p}_{F}}$
. Then we have an
$\varphi \colon \mathscr {Z}\to \frak {W=\frak W}_{U^{p}_{F}}$
. Then we have an
![]() $\mathscr {O}_{\mathscr {Z}}$
-linear injective q-expansion map
$\mathscr {O}_{\mathscr {Z}}$
-linear injective q-expansion map
characterized by the property that for every
![]() $\kappa \in \frak W^{\mathrm {cl}}$
, every closed point
$\kappa \in \frak W^{\mathrm {cl}}$
, every closed point
![]() $z\in \varphi ^{-1}(\kappa )$
, and every
$z\in \varphi ^{-1}(\kappa )$
, and every
![]() $a\in \mathbf {A}^{\infty , \times }$
, we have
$a\in \mathbf {A}^{\infty , \times }$
, we have
where the right-hand side is the p-adic q-expansion coefficient of the classical modular form
![]() ${\mathbf {f}}(z)\in (\varphi ^{*}\mathscr {S}_{\frak W})_{|z} \subset \mathrm {S}^{\mathrm {ord}}(U^{p}, \mathbf {Q}_{p}(z))$
.
${\mathbf {f}}(z)\in (\varphi ^{*}\mathscr {S}_{\frak W})_{|z} \subset \mathrm {S}^{\mathrm {ord}}(U^{p}, \mathbf {Q}_{p}(z))$
.
Moreover, the image of (2.4.4) equals the space of those sequences
![]() $(W(a))_{a}$
for which there exists a set of closed points
$(W(a))_{a}$
for which there exists a set of closed points
![]() $\Sigma \subset \varphi ^{-1}(\frak W^{\mathrm {cl}})$
that is dense in
$\Sigma \subset \varphi ^{-1}(\frak W^{\mathrm {cl}})$
that is dense in
![]() $\mathscr {Z}$
such that for all
$\mathscr {Z}$
such that for all
![]() $z\in \Sigma $
, the sequence
$z\in \Sigma $
, the sequence
![]() $(W(a)(z))_{a}$
is the p-adic q-expansion of a modular form
$(W(a)(z))_{a}$
is the p-adic q-expansion of a modular form
![]() $\mathbf {f}_{z}\in (\varphi ^{*}\mathscr {S}_{\frak W})_{|z}.$
$\mathbf {f}_{z}\in (\varphi ^{*}\mathscr {S}_{\frak W})_{|z}.$
Note that the sheaf
![]() $\mathscr {S}^{U^{p}}$
on
$\mathscr {S}^{U^{p}}$
on
![]() $\mathscr {Y}_{\mathrm {G}}$
is identified with
$\mathscr {Y}_{\mathrm {G}}$
is identified with
![]() $(\mathscr {S}_{\frak W}^{U^{p}}\otimes _{\mathscr {O}_{\frak W}}\mathscr {Y}_{\mathrm {G}})^{\mathscr {O}_{\mathscr {Y}_{\mathrm {G}}}}$
, the subsheaf of invariants for the diagonal
$(\mathscr {S}_{\frak W}^{U^{p}}\otimes _{\mathscr {O}_{\frak W}}\mathscr {Y}_{\mathrm {G}})^{\mathscr {O}_{\mathscr {Y}_{\mathrm {G}}}}$
, the subsheaf of invariants for the diagonal
![]() $\mathscr {O}_{\frak W}$
-linear action of
$\mathscr {O}_{\frak W}$
-linear action of
![]() $\mathscr {O}_{\mathscr {Y}_{\mathrm {G}}}$
. In particular, we deduce from (2.4.4) a q-expansion map
$\mathscr {O}_{\mathscr {Y}_{\mathrm {G}}}$
. In particular, we deduce from (2.4.4) a q-expansion map
Proof It suffices to construct (2.4.4) for
![]() $\mathscr {Z}=\frak W$
as the general case follows by base change. Let
$\mathscr {Z}=\frak W$
as the general case follows by base change. Let
![]() , and let
, and let
![]() $\mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Z}_{p})$
be the space of ordinary forms with
$\mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Z}_{p})$
be the space of ordinary forms with
![]() $\mathbf {Z}_{p}$
-coefficients; this is an
$\mathbf {Z}_{p}$
-coefficients; this is an
![]() $A^{\circ }$
-module and a
$A^{\circ }$
-module and a
![]() $\mathbf {Z}_{p}$
-lattice in
$\mathbf {Z}_{p}$
-lattice in
![]() $\mathscr {S}_{\frak W}^{U^{p}}(\frak W)= \mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Q}_{p})$
. For
$\mathscr {S}_{\frak W}^{U^{p}}(\frak W)= \mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Q}_{p})$
. For
![]() $\kappa \in \frak W^{\mathrm {cl}}$
, let
$\kappa \in \frak W^{\mathrm {cl}}$
, let
![]() $\mathfrak {p}_{\kappa }\subset A^{\circ }$
be the corresponding prime ideal. Let
$\mathfrak {p}_{\kappa }\subset A^{\circ }$
be the corresponding prime ideal. Let
![]() $n\in \mathbf {N}$
, and let M range among finite subsets of
$n\in \mathbf {N}$
, and let M range among finite subsets of
![]() $\frak W$
; the filtered system of ideals
$\frak W$
; the filtered system of ideals
forms a fundamental system of neighborhoods of
![]() $0\in A^{\circ }$
, i.e.,
$0\in A^{\circ }$
, i.e.,
![]() $A^{\circ }=\varprojlim _{n, M} A^{\circ }/I_{n, M}$
. The p-adic q-expansion maps
$A^{\circ }=\varprojlim _{n, M} A^{\circ }/I_{n, M}$
. The p-adic q-expansion maps
![]() $\mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Z}_{p})\otimes _{A^{\circ }}A^{\circ }/\mathfrak {p}_{\kappa }\to \mathbf {Z}_{p}(\kappa )^{\mathbf {A}^{\infty , \times }}$
yield a compatible family of maps
$\mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Z}_{p})\otimes _{A^{\circ }}A^{\circ }/\mathfrak {p}_{\kappa }\to \mathbf {Z}_{p}(\kappa )^{\mathbf {A}^{\infty , \times }}$
yield a compatible family of maps
and after taking projective limits, the desired map
![]() $\mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Z}_{p}) \to (A^{\circ })^{\mathbf {A}^{\infty , \times }}$
. It is injective by the q-expansion principle and the preservation of injectivity under inverse limits.
$\mathbf {S}^{\mathrm {ord}}(U^{p}, \mathbf {Z}_{p}) \to (A^{\circ })^{\mathbf {A}^{\infty , \times }}$
. It is injective by the q-expansion principle and the preservation of injectivity under inverse limits.
We now consider the second statement. It is clear that, for any fixed
![]() $\Sigma $
as in the lemma, the space
$\Sigma $
as in the lemma, the space
![]() $\tilde {\mathscr {S}}_{\mathscr {Z}}^{U^{p}, \Sigma } \subset \mathscr {O}_{\mathscr {Z}}^{\mathbf {A}^{\infty , \times }}$
described contains the image of (2.4.4); we show the opposite containment. We may assume that
$\tilde {\mathscr {S}}_{\mathscr {Z}}^{U^{p}, \Sigma } \subset \mathscr {O}_{\mathscr {Z}}^{\mathbf {A}^{\infty , \times }}$
described contains the image of (2.4.4); we show the opposite containment. We may assume that
![]() $\mathscr {Z}=\mathrm {Spec}\, B^{\circ }_{\mathbf {Q}_{p}}$
for a Hida ring
$\mathscr {Z}=\mathrm {Spec}\, B^{\circ }_{\mathbf {Q}_{p}}$
for a Hida ring
![]() $B^{\circ }$
, and consider (2.4.4) as a map
$B^{\circ }$
, and consider (2.4.4) as a map
For
![]() $z\in \Sigma $
, let
$z\in \Sigma $
, let
![]() $\mathfrak {p}_{z}\subset B^{\circ }$
be the corresponding prime ideal. Let
$\mathfrak {p}_{z}\subset B^{\circ }$
be the corresponding prime ideal. Let
![]() $n\in \mathbf {N}$
, and let N range among finite subsets of
$n\in \mathbf {N}$
, and let N range among finite subsets of
![]() $\Sigma $
; then the filtered system of ideals
$\Sigma $
; then the filtered system of ideals
![]() $J_{n,N}:= (p^{n})+\bigcap _{z\in N} \mathfrak {p}_{z}$
forms a fundamental system of neighborhoods of
$J_{n,N}:= (p^{n})+\bigcap _{z\in N} \mathfrak {p}_{z}$
forms a fundamental system of neighborhoods of
![]() $0\in B^{\circ }$
. By assumption, for each
$0\in B^{\circ }$
. By assumption, for each
![]() $z\in \Sigma $
, the map (2.4.6) is an isomorphism modulo
$z\in \Sigma $
, the map (2.4.6) is an isomorphism modulo
![]() $\mathfrak {p}_{z}$
; hence, it is an isomorphism modulo
$\mathfrak {p}_{z}$
; hence, it is an isomorphism modulo
![]() $J_{n, N}$
for all
$J_{n, N}$
for all
![]() $(n, N)$
, hence an isomorphism.
$(n, N)$
, hence an isomorphism.
We call elements of
![]() $\mathscr {S}_{\mathscr {Z}}^{U^{p}}$
(respectively,
$\mathscr {S}_{\mathscr {Z}}^{U^{p}}$
(respectively,
![]() $\mathscr {S}_{\mathscr {Z}}^{U^{p}}\otimes _{\mathscr {O}_{\mathscr {Z}}} \mathscr {K}(\mathscr {Z})$
)
$\mathscr {S}_{\mathscr {Z}}^{U^{p}}\otimes _{\mathscr {O}_{\mathscr {Z}}} \mathscr {K}(\mathscr {Z})$
)
![]() $\mathscr {Z}$
-adic ordinary modular cuspforms (respectively, meromorphic
$\mathscr {Z}$
-adic ordinary modular cuspforms (respectively, meromorphic
![]() $\mathscr {Z}$
-adic ordinary modular cuspforms) of weight
$\mathscr {Z}$
-adic ordinary modular cuspforms) of weight
![]() $\varphi \colon \mathscr {Z}\to \frak W$
.
$\varphi \colon \mathscr {Z}\to \frak W$
.
2.4.5 Weight-character map for
 $\mathrm {H}$
$\mathrm {H}$
Let
![]() $U_{\mathrm {H}}^{p}\subset \mathrm {H}(\mathbf {A}^{p\infty })$
be an open compact subgroup, and let
$U_{\mathrm {H}}^{p}\subset \mathrm {H}(\mathbf {A}^{p\infty })$
be an open compact subgroup, and let
as in (1.1.6). A (Hida) family for
![]() $\mathrm {H}$
is a connected component of
$\mathrm {H}$
is a connected component of
![]() $\mathscr {Y}_{\mathrm {H}}$
.
$\mathscr {Y}_{\mathrm {H}}$
.
Fix a sufficiently small open compact subgroup
![]() $U_{F, p}^{\circ , \sqrt {}}=\prod _{v\vert p} U_{F, v}^{\circ , \sqrt {}}\subset \mathscr {O}_{F,p}^{\times }$
and an injective group homomorphism
$U_{F, p}^{\circ , \sqrt {}}=\prod _{v\vert p} U_{F, v}^{\circ , \sqrt {}}\subset \mathscr {O}_{F,p}^{\times }$
and an injective group homomorphism
and let
which is now fixed as promised in Section 2.4.1. Let
![]() $\sqrt {\ }\colon U_{F, p}^{\circ } \to U_{F, p}^{\circ , \sqrt {}} $
be the (uniquely determined, up to shrinking
$\sqrt {\ }\colon U_{F, p}^{\circ } \to U_{F, p}^{\circ , \sqrt {}} $
be the (uniquely determined, up to shrinking
![]() $U_{F, p}^{\circ , \sqrt {}}$
) square root, and let
$U_{F, p}^{\circ , \sqrt {}}$
) square root, and let
![]() $j, j'\colon U_{F, p}^{\circ }\to \mathscr {O}_{E , p}^{\times }$
be the mapsFootnote
9
$j, j'\colon U_{F, p}^{\circ }\to \mathscr {O}_{E , p}^{\times }$
be the mapsFootnote
9
For any open compact
![]() $U_{E}^{p}\subset \mathbf {A}_{E}^{p\infty , \times }$
and
$U_{E}^{p}\subset \mathbf {A}_{E}^{p\infty , \times }$
and
![]() $U_{F}^{p}:= U_{E}^{p}\cap \mathbf {A}^{p\infty , \times }$
, define a map
$U_{F}^{p}:= U_{E}^{p}\cap \mathbf {A}^{p\infty , \times }$
, define a map
 $$ \begin{align}\begin{aligned} \underline{\kappa}_{\mathrm{H}}\colon \ \mathscr{Y}_{\mathrm{H}, U_{E}^{p}} &\to \frak W_{U_{F}^{p}}\\ y &\mapsto \underline{\kappa}_{\mathrm{H}}(y)=\left( \kappa_{0}=\chi_{y|[Z]_{U_{F}^{p}}}, \kappa: = \chi_{y}\circ j \right). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \underline{\kappa}_{\mathrm{H}}\colon \ \mathscr{Y}_{\mathrm{H}, U_{E}^{p}} &\to \frak W_{U_{F}^{p}}\\ y &\mapsto \underline{\kappa}_{\mathrm{H}}(y)=\left( \kappa_{0}=\chi_{y|[Z]_{U_{F}^{p}}}, \kappa: = \chi_{y}\circ j \right). \end{aligned}\end{align} $$
The set of classical points is
Note that if
![]() $y\in \mathscr {Y}_{\mathrm {H}}$
is a classical point such that
$y\in \mathscr {Y}_{\mathrm {H}}$
is a classical point such that
![]() $\underline {\kappa }_{\mathrm {H}}(y)$
has weight
$\underline {\kappa }_{\mathrm {H}}(y)$
has weight
![]() $(l_{0}, l)$
, then
$(l_{0}, l)$
, then
![]() $\chi _{y}$
has weight
$\chi _{y}$
has weight
![]() $(l_{0}, l)$
as defined in the introduction.
$(l_{0}, l)$
as defined in the introduction.
2.4.6 Hida families for
 $\mathrm {G}\times \mathrm {H}$
$\mathrm {G}\times \mathrm {H}$
These are defined as in Section 1.1.4.
2.4.7 Universal automorphic sheaf on a Hida family
Let
![]() $\mathscr {X}_{\mathrm {G}}$
be a Hida family for
$\mathscr {X}_{\mathrm {G}}$
be a Hida family for
![]() $\mathrm {G}$
, and let
$\mathrm {G}$
, and let
![]() $\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}:= \mathscr {X}_{\mathrm {G}} \cap \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}} $
. For each sufficiently small
$\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}:= \mathscr {X}_{\mathrm {G}} \cap \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}} $
. For each sufficiently small
![]() $U^{p}$
, we may view
$U^{p}$
, we may view
![]() $\mathscr {X}\subset \mathscr {Y}_{\mathrm {G}, U^{p}}$
and we define
$\mathscr {X}\subset \mathscr {Y}_{\mathrm {G}, U^{p}}$
and we define
For each
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, by Hida’s Control Theorem (see, for instance, [Reference HidaHid91, Corollary 3.3]) and the theory of newforms, we have an isomorphism of
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, by Hida’s Control Theorem (see, for instance, [Reference HidaHid91, Corollary 3.3]) and the theory of newforms, we have an isomorphism of
![]() $\mathscr {H}_{U^{p}}$
-modules,
$\mathscr {H}_{U^{p}}$
-modules,
Let
![]() $U^{p}_{\mathscr {X}_{\mathrm {G}}}$
be minimal such that
$U^{p}_{\mathscr {X}_{\mathrm {G}}}$
be minimal such that
![]() $\mathscr {X}_{\mathrm {G}}$
is a component of
$\mathscr {X}_{\mathrm {G}}$
is a component of
![]() $\mathscr {Y}_{\mathrm {G}, U^{p}_{\mathscr {X}_{\mathrm {G}}}}$
. By [Reference HidaHid91, Section 3], there is a unique
$\mathscr {Y}_{\mathrm {G}, U^{p}_{\mathscr {X}_{\mathrm {G}}}}$
. By [Reference HidaHid91, Section 3], there is a unique
(the normalised primitive form over
![]() $\mathscr {X}_{\mathrm {G}}$
) such that
$\mathscr {X}_{\mathrm {G}}$
) such that
![]() $W_{{\mathbf {f}}_{0}}(1)=1\in \mathscr {O}(\mathscr {X}_{\mathrm {G}})$
for the q-expansion map deduced from (2.4.5). Any
$W_{{\mathbf {f}}_{0}}(1)=1\in \mathscr {O}(\mathscr {X}_{\mathrm {G}})$
for the q-expansion map deduced from (2.4.5). Any
![]() $\mathbf {f} \in \Pi ^{U^{p}}$
can be written as
$\mathbf {f} \in \Pi ^{U^{p}}$
can be written as
![]() $\mathbf {f} =T \mathbf {f}_{0}$
for some Hecke operator T supported at the places
$\mathbf {f} =T \mathbf {f}_{0}$
for some Hecke operator T supported at the places
![]() $v\nmid p\infty $
such that
$v\nmid p\infty $
such that
![]() $U^{p}$
is not maximal.
$U^{p}$
is not maximal.
2.4.8 Universal Galois sheaf on a Hida family and local–global compatibility
Let
![]() $\mathscr {X}_{\mathrm {G}}$
be a Hida family for
$\mathscr {X}_{\mathrm {G}}$
be a Hida family for
![]() $\mathrm {G}$
. By results of Hida and Wiles (see [Reference DisegniDis/b, Proposition 3.2.4]), there exist an open subset
$\mathrm {G}$
. By results of Hida and Wiles (see [Reference DisegniDis/b, Proposition 3.2.4]), there exist an open subset
![]() $\mathscr {X}_{\mathrm {G}}'\subset \mathscr {X}_{\mathrm {G}}$
containing
$\mathscr {X}_{\mathrm {G}}'\subset \mathscr {X}_{\mathrm {G}}$
containing
![]() $\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and a locally free sheaf
$\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and a locally free sheaf
![]() $\mathscr {V}_{\mathrm {G}}$
of rank
$\mathscr {V}_{\mathrm {G}}$
of rank
![]() $2$
, endowed with a Galois action
$2$
, endowed with a Galois action
such that for all
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, the fiber
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, the fiber
![]() $\mathscr {V}_{\mathrm {G}|x}$
is the Galois representation attached to
$\mathscr {V}_{\mathrm {G}|x}$
is the Galois representation attached to
![]() $\pi _{x}$
by the global Langlands correspondence.
$\pi _{x}$
by the global Langlands correspondence.
Let S be a finite set of finite places of F, disjoint from
![]() $S_{p}$
, such that for all
$S_{p}$
, such that for all
![]() $v\notin S$
, the tame level
$v\notin S$
, the tame level
![]() $U^{p}=U^{Sp}U_{S}$
of
$U^{p}=U^{Sp}U_{S}$
of
![]() $\mathscr {X}_{\mathrm {G}}$
is maximal at v. We define
$\mathscr {X}_{\mathrm {G}}$
is maximal at v. We define
 $$ \begin{align}\begin{aligned} \Pi_{\mathscr{X}_{\mathrm{G}}}^{U^{Sp}}:= \varinjlim_{U^{\prime}_{S}} \Pi_{\mathscr{X}_{\mathrm{G}}}^{U^{Sp}U^{\prime}_{S}}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \Pi_{\mathscr{X}_{\mathrm{G}}}^{U^{Sp}}:= \varinjlim_{U^{\prime}_{S}} \Pi_{\mathscr{X}_{\mathrm{G}}}^{U^{Sp}U^{\prime}_{S}}, \end{aligned}\end{align} $$
which is a finitely generated
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}}}[\mathrm {G}(F_{S})]$
-module. On the other hand, [Reference DisegniDis20, Theorem 4.4.1] attaches to the restriction
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}}}[\mathrm {G}(F_{S})]$
-module. On the other hand, [Reference DisegniDis20, Theorem 4.4.1] attaches to the restriction
![]() $\mathscr {V}_{\mathrm {G}, v}:= \mathscr {V}_{\mathrm {G}|G_{F_{v}}}$
an
$\mathscr {V}_{\mathrm {G}, v}:= \mathscr {V}_{\mathrm {G}|G_{F_{v}}}$
an
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}[\mathrm {G}(F_{S})]$
-module
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}[\mathrm {G}(F_{S})]$
-module
which is torsion-free and co-Whittaker in the sense of [Reference DisegniDis20, Definition 4.2.2].
Proposition 2.4 After possibly replacing
![]() $\mathscr {X}_{\mathrm {G}}'\subset \mathscr {X}_{\mathrm {G}}$
with a smaller open subset still containing
$\mathscr {X}_{\mathrm {G}}'\subset \mathscr {X}_{\mathrm {G}}$
with a smaller open subset still containing
![]() $\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, there exists a line bundle
$\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, there exists a line bundle
![]() $\Pi ^{\circ }_{\mathscr {X}_{\mathrm {G}}'} $
over
$\Pi ^{\circ }_{\mathscr {X}_{\mathrm {G}}'} $
over
![]() $\mathscr {X}_{\mathrm {G}}'$
with trivial
$\mathscr {X}_{\mathrm {G}}'$
with trivial
![]() $\mathrm {G}(F_{S})$
-action, such that
$\mathrm {G}(F_{S})$
-action, such that
as
![]() $\mathscr {O}_{\mathscr {X}^{\prime }_{\mathrm {G}}}[\mathrm {G}(F_{S})]$
-modules.
$\mathscr {O}_{\mathscr {X}^{\prime }_{\mathrm {G}}}[\mathrm {G}(F_{S})]$
-modules.
Proof By the local–global compatibility of the Langlands correspondence for Hilbert modular forms (see [Reference CarayolCar86] or [Reference DisegniDis/b, Theorem 2.5.1]), for all
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and all places v, the
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and all places v, the
![]() $\mathrm {G}(F_{v})$
-representation
$\mathrm {G}(F_{v})$
-representation
![]() $\pi _{x,v}$
corresponds, under local Langlands, to the Weil–Deligne representation
$\pi _{x,v}$
corresponds, under local Langlands, to the Weil–Deligne representation
![]() $V_{x, v}$
attached to
$V_{x, v}$
attached to
![]() $\mathscr {V}_{\mathrm {G}|x|G_{F_{v}}}$
. Then the result follows from [Reference DisegniDis20, Theorem 4.4.3].
$\mathscr {V}_{\mathrm {G}|x|G_{F_{v}}}$
. Then the result follows from [Reference DisegniDis20, Theorem 4.4.3].
3 Theta-Eisenstein family
In this section, we define the kernel of the Rankin–Selberg convolution giving the p-adic L-function.
3.1 Weil representation
We recall the definition of the Weil representation for groups of similitudes; this subsection is largely identical to [Reference DisegniDis17, Section 3.1].
3.1.1 Local case
Let
![]() $V=(V,q)$
be a quadratic space of even dimension over a local field F of characteristic not 2. Fix a nontrivial additive character
$V=(V,q)$
be a quadratic space of even dimension over a local field F of characteristic not 2. Fix a nontrivial additive character
![]() $\psi $
of F. For
$\psi $
of F. For
![]() $u\in F^\times $
, we denote by
$u\in F^\times $
, we denote by
![]() $V_u$
the quadratic space
$V_u$
the quadratic space
![]() $(V,uq)$
. We let
$(V,uq)$
. We let
![]() $\mathrm {GL}_2(F)\times \mathrm {GO}(V)$
act on the usual space of Schwartz functions
$\mathrm {GL}_2(F)\times \mathrm {GO}(V)$
act on the usual space of Schwartz functions
![]() ${\mathcal {S}}'(V\times F^\times )$
as follows (here,
${\mathcal {S}}'(V\times F^\times )$
as follows (here,
![]() $\nu \colon \mathrm {GO}(V)\rightarrow \mathbf {G}_m$
denotes the similitude character):
$\nu \colon \mathrm {GO}(V)\rightarrow \mathbf {G}_m$
denotes the similitude character):
-
•
 $r(h)\phi (x,u)=\phi (h^{-1}x,\nu (h)u)$
for
$r(h)\phi (x,u)=\phi (h^{-1}x,\nu (h)u)$
for
 $h\in \mathrm {GO}(V)$
;
$h\in \mathrm {GO}(V)$
; -
•
 $r(n(b))\phi (x,u)=\psi (buq(x))\phi (x,u)$
for
$r(n(b))\phi (x,u)=\psi (buq(x))\phi (x,u)$
for
 $n(b)\in N(F)\subset \mathrm {GL}_2(F)$
;
$n(b)\in N(F)\subset \mathrm {GL}_2(F)$
; -
•
 $r\left (\begin {pmatrix}a&\\& d\end {pmatrix}\right )\phi (x,u)=\chi _{V_{u}}(a)|{a\over d}|^{\dim V\over 4}\phi (at, d^{-1}a^{-1}u)$
;
$r\left (\begin {pmatrix}a&\\& d\end {pmatrix}\right )\phi (x,u)=\chi _{V_{u}}(a)|{a\over d}|^{\dim V\over 4}\phi (at, d^{-1}a^{-1}u)$
; -
•
 $r(w)\phi (x,u)=\gamma (V_u)\hat {\phi }(x,u)$
for
$r(w)\phi (x,u)=\gamma (V_u)\hat {\phi }(x,u)$
for
 $w=\begin {pmatrix}&1\\-1 &\end {pmatrix}.$
$w=\begin {pmatrix}&1\\-1 &\end {pmatrix}.$
Here,
![]() $\chi _{V}=\chi _{(V,q)}$
is the quadratic character attached to V,
$\chi _{V}=\chi _{(V,q)}$
is the quadratic character attached to V,
![]() $\gamma (V,q)$
is a fourth root of unity, and
$\gamma (V,q)$
is a fourth root of unity, and
![]() $\hat {\phi }$
denotes Fourier transform in the first variable with respect to the self-dual measure for the character
$\hat {\phi }$
denotes Fourier transform in the first variable with respect to the self-dual measure for the character
![]() $\psi _{u}(x)=\psi (ux)$
. We will need to note the following facts (see, for instance, [Reference Jacquet and LanglandsJL70]):
$\psi _{u}(x)=\psi (ux)$
. We will need to note the following facts (see, for instance, [Reference Jacquet and LanglandsJL70]):
![]() $\chi _{V}$
is trivial if V is a quaternion algebra over F or
$\chi _{V}$
is trivial if V is a quaternion algebra over F or
![]() $V=F\oplus F$
, and
$V=F\oplus F$
, and
![]() $\chi _{V}=\eta $
if V is a separable quadratic extension E of F with associated character
$\chi _{V}=\eta $
if V is a separable quadratic extension E of F with associated character
![]() $\eta $
.
$\eta $
.
3.1.2 Fock model and reduced Fock model
Assume that
![]() $F=\mathbf {R}$
and V is positive definite. Then we will prefer to consider a modified version of the previous setting. Let the Fock model
$F=\mathbf {R}$
and V is positive definite. Then we will prefer to consider a modified version of the previous setting. Let the Fock model
![]() $\mathcal {S}(V\times \mathbf {R}^{\times }, \mathbf {C})$
be the space of functions spanned by those of the form
$\mathcal {S}(V\times \mathbf {R}^{\times }, \mathbf {C})$
be the space of functions spanned by those of the form
where H is a compactly supported smooth function on
![]() $\mathbf {R}^{\times }$
and P is a complex polynomial function on V. This space is not stable under the action of
$\mathbf {R}^{\times }$
and P is a complex polynomial function on V. This space is not stable under the action of
![]() $\mathrm {GL}_{2}(\mathbf {R})$
, but it is so under the restriction of the induced
$\mathrm {GL}_{2}(\mathbf {R})$
, but it is so under the restriction of the induced
![]() $(\mathfrak {gl}_{2, \mathbf {R}},\mathbf {O}_{2}(\mathbf {R}))$
-action on the usual Schwartz space (see [Reference Yuan, Zhang and ZhangYZZ12, Section 2.1.2]).
$(\mathfrak {gl}_{2, \mathbf {R}},\mathbf {O}_{2}(\mathbf {R}))$
-action on the usual Schwartz space (see [Reference Yuan, Zhang and ZhangYZZ12, Section 2.1.2]).
We will also need to consider the reduced Fock space
![]() $\overline {\mathcal {S}}(V\times \mathbf {R}^{\times })$
spanned by functions of the form
$\overline {\mathcal {S}}(V\times \mathbf {R}^{\times })$
spanned by functions of the form
where
![]() $P_{1}$
,
$P_{1}$
,
![]() $P_{2}$
are polynomial functions with rational coefficients.
$P_{2}$
are polynomial functions with rational coefficients.
By [Reference Yuan, Zhang and ZhangYZZ12, Sections 3.4.1 and 4.4.1], there is a surjective quotient map

We let
![]() $\mathcal {S}(V\times \mathbf {R}^{\times } ) \subset \mathcal {S}(V\times \mathbf {R}^{\times } , \mathbf {C})$
be the preimage of
$\mathcal {S}(V\times \mathbf {R}^{\times } ) \subset \mathcal {S}(V\times \mathbf {R}^{\times } , \mathbf {C})$
be the preimage of
![]() $\overline {\mathcal {S}}(V\times \mathbf {R}^{\times })$
. For the sake of uniformity, when F is non-archimedean, we set
$\overline {\mathcal {S}}(V\times \mathbf {R}^{\times })$
. For the sake of uniformity, when F is non-archimedean, we set
![]() $\overline {\mathcal {S}}(V\times F^{\times })=\mathcal {S}(V\times F^{\times }):= \mathcal {S}'(V\times F^{\times })$
.
$\overline {\mathcal {S}}(V\times F^{\times })=\mathcal {S}(V\times F^{\times }):= \mathcal {S}'(V\times F^{\times })$
.
3.1.3 Global case
Let
![]() $(\mathbf {V},q)$
be an even-dimensional quadratic space over the adèles
$(\mathbf {V},q)$
be an even-dimensional quadratic space over the adèles
![]() $\mathbf {A}$
of a totally real number field F, and suppose that
$\mathbf {A}$
of a totally real number field F, and suppose that
![]() $\mathbf {V}_{\infty }$
is positive definite; we say that
$\mathbf {V}_{\infty }$
is positive definite; we say that
![]() $\mathbf {V}$
is coherent if it has a model over F and incoherent otherwise. Given an
$\mathbf {V}$
is coherent if it has a model over F and incoherent otherwise. Given an
![]() $\widehat {\mathscr {O}}_{F}$
-lattice
$\widehat {\mathscr {O}}_{F}$
-lattice
![]() $\mathbf {{V}}^{\circ }\subset \mathbf {V}$
, we define the space
$\mathbf {{V}}^{\circ }\subset \mathbf {V}$
, we define the space
![]() $\mathcal {S}(\mathbf {V}\times \mathbf {A}^{\times })$
as the restricted tensor product of the corresponding local spaces, with respect to the spherical elements
$\mathcal {S}(\mathbf {V}\times \mathbf {A}^{\times })$
as the restricted tensor product of the corresponding local spaces, with respect to the spherical elements
if
![]() $\psi _{v}$
has level
$\psi _{v}$
has level
![]() $n_{v}$
. We call such
$n_{v}$
. We call such
![]() $\phi _{v}$
the standard Schwartz function at a non-archimedean place v. We define similarly the reduced space
$\phi _{v}$
the standard Schwartz function at a non-archimedean place v. We define similarly the reduced space
![]() $\overline {\mathcal {S}}(\mathbf {V}\times \mathbf {A}^{\times })$
, which admits a quotient map
$\overline {\mathcal {S}}(\mathbf {V}\times \mathbf {A}^{\times })$
, which admits a quotient map
defined by the product of the maps (3.1.1) at the infinite places and of the identity at the finite places. The Weil representation of
![]() $ \mathrm {GO}(\mathbf {V})\times \mathrm {G}(\mathbf {A}^{\infty })\times (\mathfrak {gl}_{2,F_{\infty }},\mathbf {O}(\mathbf {V}_{\infty }))$
is the restricted tensor product of the local representations.
$ \mathrm {GO}(\mathbf {V})\times \mathrm {G}(\mathbf {A}^{\infty })\times (\mathfrak {gl}_{2,F_{\infty }},\mathbf {O}(\mathbf {V}_{\infty }))$
is the restricted tensor product of the local representations.
For a quadratic space
![]() $\mathbf {V}=(\mathbf {V}, q) $
over
$\mathbf {V}=(\mathbf {V}, q) $
over
![]() $\mathbf {A}$
, we define
$\mathbf {A}$
, we define
![]() $\varepsilon (\mathbf {V})=+1$
(respectively,
$\varepsilon (\mathbf {V})=+1$
(respectively,
![]() $-1$
) if and only if there exists (respectively, does not exist) a quadratic space V over F such that
$-1$
) if and only if there exists (respectively, does not exist) a quadratic space V over F such that
![]() $V\otimes _{F}\mathbf {A}=\mathbf {V}$
.
$V\otimes _{F}\mathbf {A}=\mathbf {V}$
.
3.1.4 The quadratic spaces of interest
Let us go back to our usual notation: thus, F is our chosen totally real field and E its chosen CM quadratic extension. In this paper, we will consider the quadratic spaces
![]() $\mathbf {V}=(\mathbf {B}, q)$
, where
$\mathbf {V}=(\mathbf {B}, q)$
, where
![]() $\mathbf {B}$
is a quaternion algebra over
$\mathbf {B}$
is a quaternion algebra over
![]() $\mathbf {A}$
, definite at all the archimedean places and split at p, and endowed with an
$\mathbf {A}$
, definite at all the archimedean places and split at p, and endowed with an
![]() $\mathbf {A}$
-embedding
$\mathbf {A}$
-embedding
![]() $\mathbf {A}_{E}\hookrightarrow \mathbf {B}$
, and
$\mathbf {A}_{E}\hookrightarrow \mathbf {B}$
, and
![]() $q\colon \mathbf {B}=\mathbf {V}\to \mathbf {A}$
is its reduced norm. It has a decomposition
$q\colon \mathbf {B}=\mathbf {V}\to \mathbf {A}$
is its reduced norm. It has a decomposition
where
![]() $\mathbf {V}_{1}=\mathbf {A}_{E}$
(on which the restriction of q coincides with
$\mathbf {V}_{1}=\mathbf {A}_{E}$
(on which the restriction of q coincides with
![]() $N_{E/F}$
) and
$N_{E/F}$
) and
![]() $\mathbf {V}_{2}$
is the q-orthogonal complement. Thus,
$\mathbf {V}_{2}$
is the q-orthogonal complement. Thus,
![]() $\varepsilon (\mathbf {V})=\varepsilon (\mathbf {V}_{2})$
. We denote by
$\varepsilon (\mathbf {V})=\varepsilon (\mathbf {V}_{2})$
. We denote by
![]() $r_{1}$
the restriction of r to a representation of
$r_{1}$
the restriction of r to a representation of
![]() $\mathbf {A}_{E}^{\times }=\mathrm {GO}(\mathbf {V}_{1})$
on
$\mathbf {A}_{E}^{\times }=\mathrm {GO}(\mathbf {V}_{1})$
on
![]() $\overline {\mathcal {S}}(\mathbf {V}_{1}\times \mathbf {A}^{\times })$
.
$\overline {\mathcal {S}}(\mathbf {V}_{1}\times \mathbf {A}^{\times })$
.
For each place v, we have
 $$ \begin{align}\begin{aligned} \varepsilon({\mathbf{B}}_{v})=\varepsilon(\mathbf{V}_{v})= \begin{cases} +1, &\text{if}\ \mathbf{B}_{v}\cong M_{2}(F_{v}), \\ -1, &\text{if}\ \mathbf{B}_{v}\ \text{is a division algebra.} \end{cases} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \varepsilon({\mathbf{B}}_{v})=\varepsilon(\mathbf{V}_{v})= \begin{cases} +1, &\text{if}\ \mathbf{B}_{v}\cong M_{2}(F_{v}), \\ -1, &\text{if}\ \mathbf{B}_{v}\ \text{is a division algebra.} \end{cases} \end{aligned}\end{align} $$
We have
![]() $\varepsilon (\mathbf {V}):=\prod _{v} \varepsilon (\mathbf {V}_{v}) = (-1)^{[F:\mathbf {Q}]} \prod _{v\nmid p} \varepsilon (\mathbf {V}_{v})$
.
$\varepsilon (\mathbf {V}):=\prod _{v} \varepsilon (\mathbf {V}_{v}) = (-1)^{[F:\mathbf {Q}]} \prod _{v\nmid p} \varepsilon (\mathbf {V}_{v})$
.
3.2 Theta series
Let
![]() $\phi _{1} \in \overline {\mathcal {S}}(\mathbf {V}_{1}\times \mathbf {A}^{\times })$
. We define a function on
$\phi _{1} \in \overline {\mathcal {S}}(\mathbf {V}_{1}\times \mathbf {A}^{\times })$
. We define a function on
![]() $\mathrm {G}(\mathbf {A})\times \mathbf {A}^{\times }$
by
$\mathrm {G}(\mathbf {A})\times \mathbf {A}^{\times }$
by
It satisfies
for all
![]() $z\in {\mathbf {A}}^{\times }$
(here, we view
$z\in {\mathbf {A}}^{\times }$
(here, we view
![]() $(z, 1) \in \mathrm {G}(\mathbf {A})\times \mathbf {A}_{E}^{\times }$
).
$(z, 1) \in \mathrm {G}(\mathbf {A})\times \mathbf {A}_{E}^{\times }$
).
For a complex weight
![]() $\underline {l}$
for
$\underline {l}$
for
![]() $\mathrm {H}$
, let
$\mathrm {H}$
, let
 $$ \begin{align}\begin{aligned} \phi^{}_{1, \underline{l}, \infty} &:=\otimes_{v\vert \infty}\phi^{}_{1 , \underline{l},v}, \\ \phi^{}_{1 ,\underline{l},v}(t, u)^{} &:= \mathbf{1}_{\mathbf{R}^{+}}(u) \begin{cases} t^{l_{v}} |u|^{(-l_{0}+l_{v})/ 2}e^{-2\pi uq(t)}, & \text{if}\ l_{v}\geq 0,\\ ( \overline{t})^{-l_{v}} |u|^{(-l_{0}-l_{v})/ 2}e^{-2\pi uq(t)}, & \text{if}\ l_{v} \leq 0, \end{cases} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \phi^{}_{1, \underline{l}, \infty} &:=\otimes_{v\vert \infty}\phi^{}_{1 , \underline{l},v}, \\ \phi^{}_{1 ,\underline{l},v}(t, u)^{} &:= \mathbf{1}_{\mathbf{R}^{+}}(u) \begin{cases} t^{l_{v}} |u|^{(-l_{0}+l_{v})/ 2}e^{-2\pi uq(t)}, & \text{if}\ l_{v}\geq 0,\\ ( \overline{t})^{-l_{v}} |u|^{(-l_{0}-l_{v})/ 2}e^{-2\pi uq(t)}, & \text{if}\ l_{v} \leq 0, \end{cases} \end{aligned}\end{align} $$
and let
Define
![]() $|\underline {l}|:= (l_{0}, (| l_{v}|)_{v})$
.
$|\underline {l}|:= (l_{0}, (| l_{v}|)_{v})$
.
Lemma 3.1 The series
![]() $\theta ^{}(g, u, \phi _{1}^{\infty }; \underline {l})$
is a twisted modular form of weight
$\theta ^{}(g, u, \phi _{1}^{\infty }; \underline {l})$
is a twisted modular form of weight
![]() $(0, \underline {1})+|\underline {l} |$
.
$(0, \underline {1})+|\underline {l} |$
.
Proof The usual proof that classical theta series are automorphic shows that our
![]() $\theta $
is twisted automorphic. The archimedean component of the central character is easy to determine by (3.2.2). The weight is computed as in [Reference XueXue07, Section A1 on p. 350].
$\theta $
is twisted automorphic. The archimedean component of the central character is easy to determine by (3.2.2). The weight is computed as in [Reference XueXue07, Section A1 on p. 350].
The Whittaker–Fourier expansion of
![]() $\theta ({\underline {l}})$
is standard: for all
$\theta ({\underline {l}})$
is standard: for all
![]() $g=\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right )\in \mathrm {G}(\mathbf {A})$
with
$g=\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right )\in \mathrm {G}(\mathbf {A})$
with
![]() $y\in \mathbf {A}^{+}$
,
$y\in \mathbf {A}^{+}$
,
 $$ \begin{align}\begin{aligned} \theta(g, u, \phi_{1}^{\infty}; \underline{l}) &=\sum_{a\in F^{\times}} \sum_{x\in E^{\times}\colon uq(x)=a} r(g) \phi_{1}(x, u)\\ &= \eta(y)|y| y_{\infty}^{l_{0}+ | l |\over 2} \sum_{a\in F^{\times}} \sum_{\substack{x\in E^{\times} \\ uq(x)=a}} \phi_{1}^{\infty}(yx, y^{ -1} u) \, \mathbf{q}^{a}. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \theta(g, u, \phi_{1}^{\infty}; \underline{l}) &=\sum_{a\in F^{\times}} \sum_{x\in E^{\times}\colon uq(x)=a} r(g) \phi_{1}(x, u)\\ &= \eta(y)|y| y_{\infty}^{l_{0}+ | l |\over 2} \sum_{a\in F^{\times}} \sum_{\substack{x\in E^{\times} \\ uq(x)=a}} \phi_{1}^{\infty}(yx, y^{ -1} u) \, \mathbf{q}^{a}. \end{aligned}\end{align} $$
The following expansion result will be used in Section 3.4.
Lemma 3.2 Let
![]() $\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character of weight
$\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character of weight
![]() $\underline {l}$
, and let
$\underline {l}$
, and let
![]() $E(g,u) $
be any twisted modular form such that
$E(g,u) $
be any twisted modular form such that
![]() $E(g, u_{\infty } u)=E(g, u)$
for all
$E(g, u_{\infty } u)=E(g, u)$
for all
![]() $u_{\infty }\in F_{\infty }^{+}$
. Suppose that
$u_{\infty }\in F_{\infty }^{+}$
. Suppose that
![]() $\phi _{1}^{\infty }(0, u)=0$
for all u. Then, for all
$\phi _{1}^{\infty }(0, u)=0$
for all u. Then, for all
 $g=\left (\begin {array}{cc}y&x\\&1\end {array}\right )\in \mathrm {G}(\mathbf {A})$
, we have
$g=\left (\begin {array}{cc}y&x\\&1\end {array}\right )\in \mathrm {G}(\mathbf {A})$
, we have
 $$ \begin{align*} &\int^{*}_{E^{\times}\backslash {\mathbf{A}}_{E}^{\times} /\mathbf{A}^{\times}} \chi(t) \theta(g, u, r(t)\phi_{1}^{\infty}; \underline{l}) \star E(g,q(t) u)\, dt \\ &\quad= 4 |D_{E/F}|^{1/2} \sum_{a\in F^{\times}} \mathbf{1}_{F_{\infty}^{+}}(y_{\infty}^{-1}a) \eta(y) |y|^{1/2} y_{\infty}^{| l | +l_{0}\over 2} \int_{{\mathbf{A}}_{E}^{\infty,\times} } \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(y,y^{-1} a)\\ & \qquad\times E(g, q(t) a) \, d^{\bullet}t\, \mathbf{q}^{a}. \end{align*} $$
$$ \begin{align*} &\int^{*}_{E^{\times}\backslash {\mathbf{A}}_{E}^{\times} /\mathbf{A}^{\times}} \chi(t) \theta(g, u, r(t)\phi_{1}^{\infty}; \underline{l}) \star E(g,q(t) u)\, dt \\ &\quad= 4 |D_{E/F}|^{1/2} \sum_{a\in F^{\times}} \mathbf{1}_{F_{\infty}^{+}}(y_{\infty}^{-1}a) \eta(y) |y|^{1/2} y_{\infty}^{| l | +l_{0}\over 2} \int_{{\mathbf{A}}_{E}^{\infty,\times} } \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(y,y^{-1} a)\\ & \qquad\times E(g, q(t) a) \, d^{\bullet}t\, \mathbf{q}^{a}. \end{align*} $$
Proof We may assume that
![]() $U_{F}$
is so small that
$U_{F}$
is so small that
![]() $E(u)$
is invariant under
$E(u)$
is invariant under
![]() $u\in U_{F}$
and
$u\in U_{F}$
and
![]() $\nu _{U_{F}}=1$
. Taking fundamental domains for
$\nu _{U_{F}}=1$
. Taking fundamental domains for
![]() $\mu _{U_{F}}^{2}\backslash F^{\times }$
, the expression of interest is
$\mu _{U_{F}}^{2}\backslash F^{\times }$
, the expression of interest is
 $$ \begin{align*}\begin{aligned} &c_{U_{F}}\eta(y) |y|^{1/2} \int^{*}_{E^{\times}\backslash {\mathbf{A}}_{E}^{\times} /\mathbf{A}^{\times}} \chi(t) \sum_{u\in \mu_{U_{F}}^{2}\backslash F^{\times}} \sum_{a\in \mu_{U_{F}}^{2}\backslash F^{\times}}\sum_{x\in E^{\times}} \phi_{1}^{}(t^{-1}xy, y^{-1}q(t) u) \mathbf{1}[uq(x)=a]\\& \quad E(q(t) u,g) \, dt. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} &c_{U_{F}}\eta(y) |y|^{1/2} \int^{*}_{E^{\times}\backslash {\mathbf{A}}_{E}^{\times} /\mathbf{A}^{\times}} \chi(t) \sum_{u\in \mu_{U_{F}}^{2}\backslash F^{\times}} \sum_{a\in \mu_{U_{F}}^{2}\backslash F^{\times}}\sum_{x\in E^{\times}} \phi_{1}^{}(t^{-1}xy, y^{-1}q(t) u) \mathbf{1}[uq(x)=a]\\& \quad E(q(t) u,g) \, dt. \end{aligned}\end{align*} $$
Since the integrand is invariant under
![]() $E_{\infty }^{\times }$
, by Lemma 2.1 with
$E_{\infty }^{\times }$
, by Lemma 2.1 with
![]() $\mu =\mu _{U_{F}}$
and a change of variables
$\mu =\mu _{U_{F}}$
and a change of variables
![]() $a=uq(x)$
, this equals
$a=uq(x)$
, this equals
 $$ \begin{align*}\begin{aligned} & {2 L(1, \eta) c_{U_{F}}\over h_{E} [\mathscr{O}_{E}^{\times}:\mu_{U_{F}}]} \eta(y) |y|^{1/2} \int_{ {\mathbf{A}}_{E}^{\infty,\times} } \sum_{a\in \mu_{U_{F}}^{2}\backslash F^{\times}} \sum_{\alpha\in \mu_{U_{F}}} \\ & \qquad\qquad { \chi^{\infty}(t\alpha) \phi_{1}^{\infty}(t^{-1}\alpha^{-1}y, y^{-1}aq(t)\alpha^{2})) \mathbf{1}_{F_{\infty}^{+}}(y_{\infty}^{-1}a) y_{\infty}^{ | l | +l_{0}\over 2} \ E(g,q(t\alpha) a) \, \mathbf{q}^{\alpha^{2}a} \, d^{\bullet}t}.\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} & {2 L(1, \eta) c_{U_{F}}\over h_{E} [\mathscr{O}_{E}^{\times}:\mu_{U_{F}}]} \eta(y) |y|^{1/2} \int_{ {\mathbf{A}}_{E}^{\infty,\times} } \sum_{a\in \mu_{U_{F}}^{2}\backslash F^{\times}} \sum_{\alpha\in \mu_{U_{F}}} \\ & \qquad\qquad { \chi^{\infty}(t\alpha) \phi_{1}^{\infty}(t^{-1}\alpha^{-1}y, y^{-1}aq(t)\alpha^{2})) \mathbf{1}_{F_{\infty}^{+}}(y_{\infty}^{-1}a) y_{\infty}^{ | l | +l_{0}\over 2} \ E(g,q(t\alpha) a) \, \mathbf{q}^{\alpha^{2}a} \, d^{\bullet}t}.\end{aligned}\end{align*} $$
By the invariance properties under
![]() ${U_{F}}$
, this can be brought into the desired expression by a change of variables
${U_{F}}$
, this can be brought into the desired expression by a change of variables
![]() $a'=\alpha ^{2}a$
and the calculation
$a'=\alpha ^{2}a$
and the calculation
 $$ \begin{align*}{2 L(1, \eta) c_{U_{F}}\over h_{E} [\mathscr{O}_{E}^{\times}:\mu_{U_{F}}]} = {L(1, \eta) [\mathscr{O}_{E}^{\times}:\mathscr{O}_{F}^{\times}] \over h_{E}/h_{F}} = 4 |D_{E/F}|^{1/2},\end{align*} $$
$$ \begin{align*}{2 L(1, \eta) c_{U_{F}}\over h_{E} [\mathscr{O}_{E}^{\times}:\mu_{U_{F}}]} = {L(1, \eta) [\mathscr{O}_{E}^{\times}:\mathscr{O}_{F}^{\times}] \over h_{E}/h_{F}} = 4 |D_{E/F}|^{1/2},\end{align*} $$
which follows from the definition of
![]() $c_{U_{F}}=(2.2.5)$
and the class number formula.
$c_{U_{F}}=(2.2.5)$
and the class number formula.
3.3 Eisenstein series
Let
![]() $\mathbf {V}_{2}$
be a two-dimensional quadratic space over
$\mathbf {V}_{2}$
be a two-dimensional quadratic space over
![]() $\mathbf {A}$
, totally definite at the archimedean places. Let
$\mathbf {A}$
, totally definite at the archimedean places. Let
![]() $\phi _{2}^{}\in \overline {\mathcal {S}}(\mathbf {V}_{2}\times \mathbf {A}^{\times })$
be a Schwartz function, and let
$\phi _{2}^{}\in \overline {\mathcal {S}}(\mathbf {V}_{2}\times \mathbf {A}^{\times })$
be a Schwartz function, and let
![]() $\xi \colon F^{\times }\backslash {\mathbf {A}}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character such that
$\xi \colon F^{\times }\backslash {\mathbf {A}}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character such that
![]() $\xi _{\infty }(x) = x^{k_{0}}$
for some integer
$\xi _{\infty }(x) = x^{k_{0}}$
for some integer
![]() $k_{0}$
and for all
$k_{0}$
and for all
![]() $x\in F_{\infty }^{+}$
. Define the automorphic Eisenstein seriesFootnote
10
$x\in F_{\infty }^{+}$
. Define the automorphic Eisenstein seriesFootnote
10
 $$ \begin{align*}{E}_{r}(g, u , \phi_{2};\xi)={L^{(p\infty)}(1, \eta\xi)\over {L}^{(p\infty)}(1, \eta)}\sum_{\gamma\in P^{1}(F)\backslash SL_{2}(F)} \delta_{\xi, r} (\gamma g w_{r,p}) r(\gamma g) \phi_{2}(0,u),\end{align*} $$
$$ \begin{align*}{E}_{r}(g, u , \phi_{2};\xi)={L^{(p\infty)}(1, \eta\xi)\over {L}^{(p\infty)}(1, \eta)}\sum_{\gamma\in P^{1}(F)\backslash SL_{2}(F)} \delta_{\xi, r} (\gamma g w_{r,p}) r(\gamma g) \phi_{2}(0,u),\end{align*} $$
where (with
![]() $s\in \mathbf {C}$
)
$s\in \mathbf {C}$
)
 $$ \begin{align}\begin{aligned} \delta_{\xi, r}(g) &:=\delta_{\xi, r, 0}(g),\\ \delta_{\xi, r,s}(g) &:=\begin{cases} \xi(d)^{-1} |a/d|^{s/2} \psi(k_{0} \theta), &\textrm{if } g= \left(\begin{smallmatrix}a&b\\&d\end{smallmatrix}\right) h \textrm{ with } h=h^{\infty}r_{\theta}\in U_{p,r} SO(2, F_{\infty}), \\ 0, & \textrm{if } g\notin P(\mathbf{A}) U_{p,r} SO(2, F_{\infty}). \end{cases} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \delta_{\xi, r}(g) &:=\delta_{\xi, r, 0}(g),\\ \delta_{\xi, r,s}(g) &:=\begin{cases} \xi(d)^{-1} |a/d|^{s/2} \psi(k_{0} \theta), &\textrm{if } g= \left(\begin{smallmatrix}a&b\\&d\end{smallmatrix}\right) h \textrm{ with } h=h^{\infty}r_{\theta}\in U_{p,r} SO(2, F_{\infty}), \\ 0, & \textrm{if } g\notin P(\mathbf{A}) U_{p,r} SO(2, F_{\infty}). \end{cases} \end{aligned}\end{align} $$
(The defining sum is absolutely convergent for
![]() $\Re (s)$
sufficiently large, and otherwise it is interpreted by analytic continuation.) It satisfies
$\Re (s)$
sufficiently large, and otherwise it is interpreted by analytic continuation.) It satisfies
3.3.1 Schwartz function at
 $\infty $
$\infty $
Let
![]() $P_{k_{0}, k} \in \mathbf {R}[X]$
be the (rescaled) Laguerre polynomial
$P_{k_{0}, k} \in \mathbf {R}[X]$
be the (rescaled) Laguerre polynomial
 $$ \begin{align}\begin{aligned} P^{}_{k_{0}, k}(X) &:=(2\pi i)^{-k_{0}} (4\pi)^{-k} (k+k_{0})! \sum_{j=0}^{k} {k\choose j} {(-X)^{j}\over j!}. \\ \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} P^{}_{k_{0}, k}(X) &:=(2\pi i)^{-k_{0}} (4\pi)^{-k} (k+k_{0})! \sum_{j=0}^{k} {k\choose j} {(-X)^{j}\over j!}. \\ \end{aligned}\end{align} $$
For
![]() $k=(k_{0}, (k_{v}))\in \mathbf {Z}\times \mathbf {Z}_{\geq 0}^{{\Sigma _{\infty }}}$
such that
$k=(k_{0}, (k_{v}))\in \mathbf {Z}\times \mathbf {Z}_{\geq 0}^{{\Sigma _{\infty }}}$
such that
![]() $k_{v}+k_{0}\geq 0$
for all v, define
$k_{v}+k_{0}\geq 0$
for all v, define
where
![]() $\phi ^{}_{2, \infty , k}=\otimes _{v\vert \infty }\phi ^{}_{2, v, k_{v}}$
with
$\phi ^{}_{2, \infty , k}=\otimes _{v\vert \infty }\phi ^{}_{2, v, k_{v}}$
with
The series
![]() ${E}_{r}(\phi _{2}^{\infty }; \xi , k)$
belongs to
${E}_{r}(\phi _{2}^{\infty }; \xi , k)$
belongs to
![]() $N_{\mathrm {tw}, (-k_{0}, k+k_{0})}^{\leq k}( \mathbf {C})$
.
$N_{\mathrm {tw}, (-k_{0}, k+k_{0})}^{\leq k}( \mathbf {C})$
.
3.3.2 Whittaker–Fourier expansion
The following standard result is essentially [Reference DisegniDis17, Proposition 3.2.1].
Proposition 3.3 We have
where
with, for each v and
![]() $a\in F_{v}$
,
$a\in F_{v}$
,
 $$ \begin{align*} & W_{a,r,v}(g,u, \phi_{2,v};\xi_{v})\\ & \quad = { L^{(p\infty)}(1, \eta_{v}\xi_{v}) \over L^{(p\infty)}(1, \eta_{v})} \int_{F_{v}}\delta_{\xi,r, v}(wn(b)gw_{r,v}) r(wn(b)g ) \phi_{2,v }(0,u)\psi_{v}(-ab) \, db. \end{align*} $$
$$ \begin{align*} & W_{a,r,v}(g,u, \phi_{2,v};\xi_{v})\\ & \quad = { L^{(p\infty)}(1, \eta_{v}\xi_{v}) \over L^{(p\infty)}(1, \eta_{v})} \int_{F_{v}}\delta_{\xi,r, v}(wn(b)gw_{r,v}) r(wn(b)g ) \phi_{2,v }(0,u)\psi_{v}(-ab) \, db. \end{align*} $$
Here,
![]() $L^{(p\infty )}(s, \xi ^{\prime }_{v}):=L(s, \xi ^{\prime }_{v})$
if
$L^{(p\infty )}(s, \xi ^{\prime }_{v}):=L(s, \xi ^{\prime }_{v})$
if
![]() $v\nmid p\infty $
and
$v\nmid p\infty $
and
![]() $L^{(p \infty )}(s,\xi ^{\prime }_{v}):=1$
if
$L^{(p \infty )}(s,\xi ^{\prime }_{v}):=1$
if
![]() $v\vert p\infty $
, and we use the convention that
$v\vert p\infty $
, and we use the convention that
![]() $r_{v}=0$
if
$r_{v}=0$
if
![]() $v\nmid p$
.
$v\nmid p$
.
(Note that the functions
![]() $W_{a,r}(\phi _{2}, \xi )$
correspond to the
$W_{a,r}(\phi _{2}, \xi )$
correspond to the
![]() $W^{\mathbf {C}}_{E_{r}(\phi _{2}, \xi ), a}$
of Section 2.2.2. We prefer to use lighter notation in this section.)
$W^{\mathbf {C}}_{E_{r}(\phi _{2}, \xi ), a}$
of Section 2.2.2. We prefer to use lighter notation in this section.)
We choose convenient normalizations for the local Whittaker functions: let
![]() $\gamma _{u, v}=\gamma (\mathbf {V}_{2,v}, uq)$
be the Weil index, and for
$\gamma _{u, v}=\gamma (\mathbf {V}_{2,v}, uq)$
be the Weil index, and for
![]() $a\in F_{v}^{\times }$
, set
$a\in F_{v}^{\times }$
, set
Then, for the global Whittaker functions, we have
 $$ \begin{align} W_{a,r}(g,u, \phi_{2}; \xi)={-\varepsilon(\mathbf{V}_{2}) \over L^{(p)}(1, \eta)} \prod_{v}W^{\circ}_{a,r,v}(g,u, \phi_{2,v}; \xi_{v}) \end{align} $$
$$ \begin{align} W_{a,r}(g,u, \phi_{2}; \xi)={-\varepsilon(\mathbf{V}_{2}) \over L^{(p)}(1, \eta)} \prod_{v}W^{\circ}_{a,r,v}(g,u, \phi_{2,v}; \xi_{v}) \end{align} $$
if
![]() $a\in F^{\times }$
, where
$a\in F^{\times }$
, where
![]() $\varepsilon (\mathbf {V}_{2})=\prod _{v}\gamma _{u, v}$
equals
$\varepsilon (\mathbf {V}_{2})=\prod _{v}\gamma _{u, v}$
equals
![]() $-1$
if
$-1$
if
![]() $\mathbf {V}_{2}$
is coherent or
$\mathbf {V}_{2}$
is coherent or
![]() $+1$
if
$+1$
if
![]() $\mathbf { V}_{2}$
is incoherent. We similarly define
$\mathbf { V}_{2}$
is incoherent. We similarly define
![]() $W_{0, r}^{\circ }(g, u, \phi _{2}, \xi ) $
by the identity
$W_{0, r}^{\circ }(g, u, \phi _{2}, \xi ) $
by the identity
 $$ \begin{align} W_{0, r}^{}(g, u, \phi_{2}; \xi) = {-\varepsilon(\mathbf{V}_{2}) \over L^{(p)}(1, \eta)} W_{0, r}^{\circ}(g, u, \phi_{2}; \xi). \end{align} $$
$$ \begin{align} W_{0, r}^{}(g, u, \phi_{2}; \xi) = {-\varepsilon(\mathbf{V}_{2}) \over L^{(p)}(1, \eta)} W_{0, r}^{\circ}(g, u, \phi_{2}; \xi). \end{align} $$
A simple calculation shows that for all v and
![]() $a\neq 0$
,
$a\neq 0$
,
We will sometimes drop
![]() $\phi _{2, v}$
from the notation.
$\phi _{2, v}$
from the notation.
The following sufficient condition for cuspidality will simplify matters a little later on.
Lemma 3.4 Assume that there is a place
![]() $v\nmid p\infty $
, at which
$v\nmid p\infty $
, at which
![]() $\xi _{v}$
is unramified, such that
$\xi _{v}$
is unramified, such that
for all u. Then, for all
![]() $g={\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right )}$
with
$g={\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right )}$
with
![]() $y\in \mathbf {A}^{+}, x\in \mathbf {A}$
, we have
$y\in \mathbf {A}^{+}, x\in \mathbf {A}$
, we have
Proof This is a special case of [Reference Yuan, Zhang and ZhangYZZ12, Proposition 6.10].
3.3.3 Archimedean Whittaker functions
We compute them explicitly based on our explicit choice of Schwartz function.
Lemma 3.5 Let
![]() $v\vert \infty $
, let
$v\vert \infty $
, let
![]() $\xi _{v}(x)=x^{k_{0}}$
for some
$\xi _{v}(x)=x^{k_{0}}$
for some
![]() $k_{0}\in \mathbf {Z}$
, and let
$k_{0}\in \mathbf {Z}$
, and let
![]() $\phi _{2,v}(x, u):= \mathbf {1}_{\mathbf {R}^{+}}(u) (uq(x))^{k}e^{-2\pi uq(x)}$
for some
$\phi _{2,v}(x, u):= \mathbf {1}_{\mathbf {R}^{+}}(u) (uq(x))^{k}e^{-2\pi uq(x)}$
for some
![]() $k\in \mathbf {Z}_{\geq 0}$
with
$k\in \mathbf {Z}_{\geq 0}$
with
![]() $k\geq -k_{0}$
. Let
$k\geq -k_{0}$
. Let
![]() $a\in \mathbf {R}^{\times }$
. Then
$a\in \mathbf {R}^{\times }$
. Then
 $$ \begin{align*} W_{a,v}^{\circ}( 1,u, \phi_{2,v, k_{v}};\xi_{v}) = \begin{cases} \displaystyle 2 (2\pi i)^{k_{0}} {k! \over (k+k_{0})!} a^{k+k_{0}} e^{-2\pi a}, & \text{if}\ a,u>0,\\ 0, & \text{if}\ a<0\ \text{or}\ u<0. \end{cases} \end{align*} $$
$$ \begin{align*} W_{a,v}^{\circ}( 1,u, \phi_{2,v, k_{v}};\xi_{v}) = \begin{cases} \displaystyle 2 (2\pi i)^{k_{0}} {k! \over (k+k_{0})!} a^{k+k_{0}} e^{-2\pi a}, & \text{if}\ a,u>0,\\ 0, & \text{if}\ a<0\ \text{or}\ u<0. \end{cases} \end{align*} $$
Proof We drop the subscript v and write
![]() $\delta _{\xi , s}$
for
$\delta _{\xi , s}$
for
![]() $\delta _{\xi , r,s}$
. We have
$\delta _{\xi , r,s}$
. We have
 $$ \begin{align*}wn(b) = \left(\begin{array}{@{}cc@{}}(1 +b^{2})^{-1/2} &-b(1 +b^{2})^{-1/2 }\\& {(1 +b^{2})^{1/2} } r_{\theta_{b}}\end{array}\right) \end{align*} $$
$$ \begin{align*}wn(b) = \left(\begin{array}{@{}cc@{}}(1 +b^{2})^{-1/2} &-b(1 +b^{2})^{-1/2 }\\& {(1 +b^{2})^{1/2} } r_{\theta_{b}}\end{array}\right) \end{align*} $$
with
![]() $e^{ i \theta _{b}} = (i-b)/ {(1 +b^{2})^{1/2} }$
. Then
$e^{ i \theta _{b}} = (i-b)/ {(1 +b^{2})^{1/2} }$
. Then
![]() $\delta _{\xi ,s} (wn(b)) = i^{k_{0}} (1+b^{2})^{-s/2} (1- ib)^{-k_{0}}$
. Since
$\delta _{\xi ,s} (wn(b)) = i^{k_{0}} (1+b^{2})^{-s/2} (1- ib)^{-k_{0}}$
. Since
![]() $L(1,\eta )=\pi ^{-1} $
and
$L(1,\eta )=\pi ^{-1} $
and
![]() $\gamma _{v}=i$
, we have
$\gamma _{v}=i$
, we have
 $$ \begin{align}\begin{aligned} & i^{-k_{0}}W_{a}^{\circ}(s, 1,u, \phi_{2, k})\\ & \quad := i^{-1} \pi^{-1}\int_{\mathbf{R}} \delta_{\xi, s}(w n(b) ) r(wn(b))\phi_{2, k}(0, u)\psi(-ab) \, db\\ & \quad = \pi^{-1}\int_{\mathbf{R}} (1+b^{2})^{-s/2} (1- ib)^{-k_{0}} \int_{\mathbf{C}} \phi_{2, k}(x, u) \psi(ubq(x)) d_{u}x \, \psi(-ab) db\\ & \quad = \pi^{-1} \int_{\mathbf{R}} (1+b^{2})^{-s/2} (1- ib)^{-k_{0}} \int_{\mathbf{C}} u^{k+1} q(x)^{k} e^{-2\pi u q(x)} \psi(ubq(x)) d_{1}x\, \psi(-ab) db, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} & i^{-k_{0}}W_{a}^{\circ}(s, 1,u, \phi_{2, k})\\ & \quad := i^{-1} \pi^{-1}\int_{\mathbf{R}} \delta_{\xi, s}(w n(b) ) r(wn(b))\phi_{2, k}(0, u)\psi(-ab) \, db\\ & \quad = \pi^{-1}\int_{\mathbf{R}} (1+b^{2})^{-s/2} (1- ib)^{-k_{0}} \int_{\mathbf{C}} \phi_{2, k}(x, u) \psi(ubq(x)) d_{u}x \, \psi(-ab) db\\ & \quad = \pi^{-1} \int_{\mathbf{R}} (1+b^{2})^{-s/2} (1- ib)^{-k_{0}} \int_{\mathbf{C}} u^{k+1} q(x)^{k} e^{-2\pi u q(x)} \psi(ubq(x)) d_{1}x\, \psi(-ab) db, \end{aligned}\end{align} $$
where we recall that
![]() $d_{u}x= |u| d_{1}x$
and
$d_{u}x= |u| d_{1}x$
and
![]() $d_{1}x$
is twice the usual Lebesgue measure. The integral over
$d_{1}x$
is twice the usual Lebesgue measure. The integral over
![]() $\mathbf {C}$
is
$\mathbf {C}$
is
 $$ \begin{align*}2u^{k+1}\sum_{j=0}^{k} \int_{\mathbf{R}} \int_{\mathbf{R}}{k\choose j} x_{1}^{2j}x_{2}^{k-j} e^{-2\pi u (1-ib) (x_{1}^{2}+x_{2}^{2})} dx_{1}dx_{2}.\end{align*} $$
$$ \begin{align*}2u^{k+1}\sum_{j=0}^{k} \int_{\mathbf{R}} \int_{\mathbf{R}}{k\choose j} x_{1}^{2j}x_{2}^{k-j} e^{-2\pi u (1-ib) (x_{1}^{2}+x_{2}^{2})} dx_{1}dx_{2}.\end{align*} $$
Since
![]() $\int _{\mathbf {R}} x^{2j}e^{-Ax^{2}} \, dx = {A^{-j-1/2}\Gamma (j+1/2)}$
, this equals
$\int _{\mathbf {R}} x^{2j}e^{-Ax^{2}} \, dx = {A^{-j-1/2}\Gamma (j+1/2)}$
, this equals
 $$ \begin{align*}\begin{aligned} & 2 u^{k} \sum_{j=0}^{k} {k \choose j} \Gamma(j+1/2) \Gamma(k-j+1/2)\cdot (2\pi u )^{-k-1} (1-ib)^{-k-1} = 2^{-k} \pi^{-k} k! \, (1-ib)^{-k-1} \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} & 2 u^{k} \sum_{j=0}^{k} {k \choose j} \Gamma(j+1/2) \Gamma(k-j+1/2)\cdot (2\pi u )^{-k-1} (1-ib)^{-k-1} = 2^{-k} \pi^{-k} k! \, (1-ib)^{-k-1} \end{aligned}\end{align*} $$
by the combinatorial identity (see Appendix A)
 $$ \begin{align}\begin{aligned} \sum_{j=0}^{k} {k \choose j} \Gamma(j+1/2) \Gamma(k-j+1/2) = \pi k!.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \sum_{j=0}^{k} {k \choose j} \Gamma(j+1/2) \Gamma(k-j+1/2) = \pi k!.\end{aligned}\end{align} $$
Therefore, when
![]() $u>0$
,
$u>0$
,
The integral is the same one appearing in [Reference Yuan, Zhang and ZhangYZZ12, bottom of p. 55] with
![]() $d=2+2k+2k_{0}$
. By [Reference Yuan, Zhang and ZhangYZZ12, Proposition 2.11] (whose normalization differs from ours by
$d=2+2k+2k_{0}$
. By [Reference Yuan, Zhang and ZhangYZZ12, Proposition 2.11] (whose normalization differs from ours by
![]() $L(1, \eta _{v}\xi _{v})=\pi i $
), we find
$L(1, \eta _{v}\xi _{v})=\pi i $
), we find
 $$ \begin{align*}W_{a}^{\circ}(0, 1,u, \phi_{2, k}) &= i^{k_{0}} 2^{-k} \pi^{-k-1} k! {(2\pi)^{1+k+k_{0}}\over \Gamma(1+k+k_{0})} a^{k+k_{0}} e^{-2\pi a}\\ &= 2 (2\pi i)^{k_{0}} {k! \over (k+k_{0})!} a^{k+k_{0}} e^{-2\pi a}\end{align*} $$
$$ \begin{align*}W_{a}^{\circ}(0, 1,u, \phi_{2, k}) &= i^{k_{0}} 2^{-k} \pi^{-k-1} k! {(2\pi)^{1+k+k_{0}}\over \Gamma(1+k+k_{0})} a^{k+k_{0}} e^{-2\pi a}\\ &= 2 (2\pi i)^{k_{0}} {k! \over (k+k_{0})!} a^{k+k_{0}} e^{-2\pi a}\end{align*} $$
if
![]() $a, u>0$
, as well as simpler formulas implying the desired ones in the other cases.
$a, u>0$
, as well as simpler formulas implying the desired ones in the other cases.
We deduce the following. Let
 $$ \begin{align}\begin{aligned} Q_{k_{0}, k}(X)= \sum_{j=0}^{k} {k\choose j} {(k+k_{0})! \over (j+k_{0})!} (-X)^{k-j},\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} Q_{k_{0}, k}(X)= \sum_{j=0}^{k} {k\choose j} {(k+k_{0})! \over (j+k_{0})!} (-X)^{k-j},\end{aligned}\end{align} $$
which satisfies
![]() $Q_{k_{0}, k}(0)=1$
.
$Q_{k_{0}, k}(0)=1$
.
Proposition 3.6 Let
![]() $v\vert \infty $
, let
$v\vert \infty $
, let
![]() $a\in \mathbf {R}$
, and let
$a\in \mathbf {R}$
, and let
![]() $k_{0}\in \mathbf {Z}$
and
$k_{0}\in \mathbf {Z}$
and
![]() $k\in \mathbf {Z}_{\geq 0}$
with
$k\in \mathbf {Z}_{\geq 0}$
with
![]() $k\geq -k_{0}$
. Then, for
$k\geq -k_{0}$
. Then, for
![]() $a\neq 0$
, we have
$a\neq 0$
, we have
if
![]() $ay>0$
,
$ay>0$
,
![]() $uy>0$
, and
$uy>0$
, and
![]() $W_{a,v}(0, \left (\begin {smallmatrix}y&\\&1\end {smallmatrix}\right ),u, \phi _{2,v ,k_{v}}; \xi _{v})=0$
otherwise.
$W_{a,v}(0, \left (\begin {smallmatrix}y&\\&1\end {smallmatrix}\right ),u, \phi _{2,v ,k_{v}}; \xi _{v})=0$
otherwise.
Proof After recalling the definition of
![]() $P_{k_{0}, k}$
in (3.3.2), by Lemma 3.5 and (3.3.6), we find the asserted vanishing and that for
$P_{k_{0}, k}$
in (3.3.2), by Lemma 3.5 and (3.3.6), we find the asserted vanishing and that for
![]() $ay, uy>0$
we have (dropping subscripts v):
$ay, uy>0$
we have (dropping subscripts v):
 $$ \begin{align*} & W_{a,v}( \left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right),u, \phi_{2, k}; \xi)\\ & \quad = \eta\xi^{-1}(y) |y|^{1/2} \cdot 2 (4\pi)^{-k} (-4\pi)^{-k_{0}} (k+k_{0})! \sum_{j=0}^{k} {k\choose j} {(k+k_{0})! \over (j+k_{0})!} (-4\pi ay)^{j+k_{0}} e^{-2\pi ay} ,\end{align*} $$
$$ \begin{align*} & W_{a,v}( \left(\begin{smallmatrix}y&\\&1\end{smallmatrix}\right),u, \phi_{2, k}; \xi)\\ & \quad = \eta\xi^{-1}(y) |y|^{1/2} \cdot 2 (4\pi)^{-k} (-4\pi)^{-k_{0}} (k+k_{0})! \sum_{j=0}^{k} {k\choose j} {(k+k_{0})! \over (j+k_{0})!} (-4\pi ay)^{j+k_{0}} e^{-2\pi ay} ,\end{align*} $$
which is equal to the asserted formula.
Corollary 3.7 Let
![]() $\xi \colon F^{\times }\backslash \mathbf {A}^{\times }\to \mathbf {C}^{\times }$
with
$\xi \colon F^{\times }\backslash \mathbf {A}^{\times }\to \mathbf {C}^{\times }$
with
![]() $\xi (x_{\infty })=x_{\infty }^{k_{0}}$
for some
$\xi (x_{\infty })=x_{\infty }^{k_{0}}$
for some
![]() $k_{0}\in \mathbf {Z}$
. For each
$k_{0}\in \mathbf {Z}$
. For each
![]() $k\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
with
$k\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
with
![]() $k\geq -k_{0}$
, we have
$k\geq -k_{0}$
, we have
3.3.4 Schwartz function at p
Let
![]() $U_{F,p}^{\circ } \subset \mathscr {O}_{F, p}^{\times }$
be as fixed in Section 2.4.5, and let
$U_{F,p}^{\circ } \subset \mathscr {O}_{F, p}^{\times }$
be as fixed in Section 2.4.5, and let
![]() $\kappa _{2}'\colon U_{F,p}^{\circ }\to \mathbf {C}^{\times }$
be a smooth character. We define
$\kappa _{2}'\colon U_{F,p}^{\circ }\to \mathbf {C}^{\times }$
be a smooth character. We define
where
![]() $\mathbf {V}^{\circ }_{2,p}\subset \mathbf {V}_{2,p}$
is a fixed
$\mathbf {V}^{\circ }_{2,p}\subset \mathbf {V}_{2,p}$
is a fixed
![]() $\mathscr {O}_{F, p}$
-lattice and
$\mathscr {O}_{F, p}$
-lattice and
 $\displaystyle \delta _{U_{F,p}^{\circ }}(u):= {\mathrm {vol}(\mathscr {O}_{F, p}^{\times })\over \mathrm {vol}(U_{F,p}^{\circ })}\cdot \mathbf {1}_{U_{F,p}^{\circ }}(u)$
. It is invariant under
$\displaystyle \delta _{U_{F,p}^{\circ }}(u):= {\mathrm {vol}(\mathscr {O}_{F, p}^{\times })\over \mathrm {vol}(U_{F,p}^{\circ })}\cdot \mathbf {1}_{U_{F,p}^{\circ }}(u)$
. It is invariant under
![]() $N(\mathscr {O}_{F,p})$
.
$N(\mathscr {O}_{F,p})$
.
Let
and denote its normalized Whittaker functions by
depending on the place v, we will drop the unnecessary elements from the notation.
3.3.5 Non-archimedean Whittaker functions
We study the functions
![]() $W_{a,v}^{\circ }$
and the q-expansion of
$W_{a,v}^{\circ }$
and the q-expansion of
![]() $E_{r}$
.
$E_{r}$
.
Proposition 3.8 Let v be a non-archimedean place of F.
-
(1) If
 $v\nmid p$
, then
$v\nmid p$
, then
 $W_{a,v,r}^{\circ }=W_{a,v}^{\circ }$
does not depend on r, and for all
$W_{a,v,r}^{\circ }=W_{a,v}^{\circ }$
does not depend on r, and for all
 $a\in F_{v}$
, where
$a\in F_{v}$
, where $$ \begin{align*}W_{a,v}^{\circ}(1,u, \xi)=|d_{v}|^{1/2}L(1, \eta_{v}\xi_{v}) (1-\xi_{v}(\varpi_{v})) \sum_{n=0}^{\infty} \xi_{F,v}(\varpi_{v})^{n} q_{F,v}^{n}\int_{D_{n}(a)}\phi_{2,v}(x_{2},u) \, d_{u}x_{2},\end{align*} $$
$$ \begin{align*}W_{a,v}^{\circ}(1,u, \xi)=|d_{v}|^{1/2}L(1, \eta_{v}\xi_{v}) (1-\xi_{v}(\varpi_{v})) \sum_{n=0}^{\infty} \xi_{F,v}(\varpi_{v})^{n} q_{F,v}^{n}\int_{D_{n}(a)}\phi_{2,v}(x_{2},u) \, d_{u}x_{2},\end{align*} $$
 $d_{u}x_{2}$
is the self-dual measure on
$d_{u}x_{2}$
is the self-dual measure on
 $(\mathbf {V}_{2,v}, uq)$
and (When the sum is infinite, it is to be understood in the sense of analytic continuation from characters
$(\mathbf {V}_{2,v}, uq)$
and (When the sum is infinite, it is to be understood in the sense of analytic continuation from characters $$ \begin{align*}D_{n}(a)=\{ x_{2}\in \mathbf{V}_{2,v}\, |\, uq(x_{2})\in a+p_{v}^{n}d_{v}^{-1}\}.\end{align*} $$
$$ \begin{align*}D_{n}(a)=\{ x_{2}\in \mathbf{V}_{2,v}\, |\, uq(x_{2})\in a+p_{v}^{n}d_{v}^{-1}\}.\end{align*} $$
 $\xi |\cdot |^{s}$
with
$\xi |\cdot |^{s}$
with
 $s>0$
.)
$s>0$
.)
-
(2) For all finite places v,
 $|d|_{v}^{-3/2}|D_{v}|^{-1/2}W_{a,v}^{\circ }(1, u, \xi )\in \mathbf {Q}[\xi , \phi _{2,v}]$
, and for almost all v, we have
$|d|_{v}^{-3/2}|D_{v}|^{-1/2}W_{a,v}^{\circ }(1, u, \xi )\in \mathbf {Q}[\xi , \phi _{2,v}]$
, and for almost all v, we have  $$ \begin{align*}|d|_{v}^{-3/2}|D_{v}|^{-1/2}W^{\circ}_{a,v}(1,u, \xi)= \begin{cases} 1, & \textrm{ if } v(a)\geq - v(d_{v})\textrm{ and } v(u)=-v(d_{v}), \\ 0, & \textrm{ otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}|d|_{v}^{-3/2}|D_{v}|^{-1/2}W^{\circ}_{a,v}(1,u, \xi)= \begin{cases} 1, & \textrm{ if } v(a)\geq - v(d_{v})\textrm{ and } v(u)=-v(d_{v}), \\ 0, & \textrm{ otherwise.} \end{cases}\end{align*} $$
-
(3) If
 $v\vert p$
, then
$v\vert p$
, then  $$ \begin{align*}\kern-8pt W_{a,r, v}^{\circ}(1, u; \xi, \kappa_{2}')= \begin{cases} |d_{v}|^{3/2}|D_{v}|^{1/2} \xi_{v}(-1) \kappa_{2,v}'(u), & \textrm{ if } v(a)\geq -v(d) \textrm{ and } u\in U_{F, v}^{\circ}, \\ 0, & \textrm{ otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\kern-8pt W_{a,r, v}^{\circ}(1, u; \xi, \kappa_{2}')= \begin{cases} |d_{v}|^{3/2}|D_{v}|^{1/2} \xi_{v}(-1) \kappa_{2,v}'(u), & \textrm{ if } v(a)\geq -v(d) \textrm{ and } u\in U_{F, v}^{\circ}, \\ 0, & \textrm{ otherwise.} \end{cases} \end{align*} $$
Proof See [Reference DisegniDis17, Proposition 3.2.3 and Lemma 3.2.4] for parts 1 and 2. For part 3, we drop subscripts v and compute
(the latter if
![]() $b\in \mathscr {O}_{F}$
), so that
$b\in \mathscr {O}_{F}$
), so that
which gives the asserted value.
Corollary 3.9 For
![]() $g=\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right ) $
with
$g=\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right ) $
with
![]() $y\in \mathbf {A}^{+}$
and
$y\in \mathbf {A}^{+}$
and
![]() $x\in \mathbf {A}$
, we have
$x\in \mathbf {A}$
, we have
 $$ \begin{align*} &{E}_{r} (g,u,\phi_{2}^{\infty}; \xi, k) = {-\varepsilon(\mathbf{V}_{2}) \over L^{(p)}(1, \eta)} \eta\xi^{-1}(y) |y|^{1/2} \\ &\cdot \left(W_{0}^{\circ}(y, u)+ \sum_{a\in F^{+}} 2^{[F:\mathbf{Q}]} (ay_{\infty})^{k+k_{0}} W_{a,r}^{\circ , \infty}(0, 1, y^{-1}u, \phi_{2}, \xi) Q_{k_{0}, k}((4\pi a y_{\infty})^{-1}) \, \mathbf{q}^{a}\right), \end{align*} $$
$$ \begin{align*} &{E}_{r} (g,u,\phi_{2}^{\infty}; \xi, k) = {-\varepsilon(\mathbf{V}_{2}) \over L^{(p)}(1, \eta)} \eta\xi^{-1}(y) |y|^{1/2} \\ &\cdot \left(W_{0}^{\circ}(y, u)+ \sum_{a\in F^{+}} 2^{[F:\mathbf{Q}]} (ay_{\infty})^{k+k_{0}} W_{a,r}^{\circ , \infty}(0, 1, y^{-1}u, \phi_{2}, \xi) Q_{k_{0}, k}((4\pi a y_{\infty})^{-1}) \, \mathbf{q}^{a}\right), \end{align*} $$
where
![]() $W_{a,r}^{\circ , \infty }(0, 1, u, \phi _{2}; \xi ) = \prod _{v\nmid \infty }W_{a,r,v}^{\circ }(0, 1, y^{-1}u, \phi _{2, v}; \xi )$
.
$W_{a,r}^{\circ , \infty }(0, 1, u, \phi _{2}; \xi ) = \prod _{v\nmid \infty }W_{a,r,v}^{\circ }(0, 1, y^{-1}u, \phi _{2, v}; \xi )$
.
Let
![]() $\phi _{2}^{p\infty }$
satisfy (3.3.7), so that by Lemma 3.4, the corresponding Eisenstein series is cuspidal. For
$\phi _{2}^{p\infty }$
satisfy (3.3.7), so that by Lemma 3.4, the corresponding Eisenstein series is cuspidal. For
![]() $\xi $
a locally algebraic p-adic character of
$\xi $
a locally algebraic p-adic character of
![]() $\mathbf {A}^{\times }$
of weight
$\mathbf {A}^{\times }$
of weight
![]() $k_{0}$
, consider the (bounded) sequence of coefficients in
$k_{0}$
, consider the (bounded) sequence of coefficients in
![]() $\mathbf {Q}_{p}(\xi )$
$\mathbf {Q}_{p}(\xi )$
where
![]() $\lambda = {-\varepsilon (\mathbf {V}_{2}) / |D_{E/F}|^{1/2} L^{(p)}(1, \eta )} $
. This is the p-adic q-expansion attached to
$\lambda = {-\varepsilon (\mathbf {V}_{2}) / |D_{E/F}|^{1/2} L^{(p)}(1, \eta )} $
. This is the p-adic q-expansion attached to
![]() $E_{r}$
. Analogously to Corollary 3.7, we have
$E_{r}$
. Analogously to Corollary 3.7, we have
3.3.6 p-adic interpolation of Whittaker functions
For a place
![]() $v\nmid p\infty $
of F, denote
$v\nmid p\infty $
of F, denote
![]() $\mathscr {Y}_{v}:= \mathrm {Spec}\, \mathbf {Q}_{p}[F_{v}^{\times }]$
and (for a later use)
$\mathscr {Y}_{v}:= \mathrm {Spec}\, \mathbf {Q}_{p}[F_{v}^{\times }]$
and (for a later use)
![]() $\mathscr {Y}_{\mathrm {H}, v}:=\mathrm {Spec}\, \mathbf {Q}_{p}[E_{v}^{\times }]$
, the spaces of characters of
$\mathscr {Y}_{\mathrm {H}, v}:=\mathrm {Spec}\, \mathbf {Q}_{p}[E_{v}^{\times }]$
, the spaces of characters of
![]() $F_{v}^{\times }$
(respectively,
$F_{v}^{\times }$
(respectively,
![]() $E_{v}^{\times }$
). We say that a meromorphic function
$E_{v}^{\times }$
). We say that a meromorphic function
![]() $\Phi $
on an integral scheme has poles controlled by the (nonzero) meromorphic function
$\Phi $
on an integral scheme has poles controlled by the (nonzero) meromorphic function
![]() $\Phi '$
if
$\Phi '$
if
![]() $\Phi /\Phi '$
is regular.
$\Phi /\Phi '$
is regular.
Proposition 3.10 Let
![]() $v\nmid p\infty $
. For each
$v\nmid p\infty $
. For each
![]() $a\in F_{v}^{\times }$
,
$a\in F_{v}^{\times }$
,
![]() $y\in F_{v}^{\times }$
, and
$y\in F_{v}^{\times }$
, and
![]() $\phi _{2,v}\in \mathcal {S}(\mathbf { V}_{2}^{p\infty }\times \mathbf {A}^{p\infty , \times }, \mathbf {Q}_{p})$
, there is a meromorphic function
$\phi _{2,v}\in \mathcal {S}(\mathbf { V}_{2}^{p\infty }\times \mathbf {A}^{p\infty , \times }, \mathbf {Q}_{p})$
, there is a meromorphic function
regular if
![]() $\phi _{2, v}$
is standard and otherwise with poles controlled by
$\phi _{2, v}$
is standard and otherwise with poles controlled by
![]() $L(1,\eta _{v}\xi _{v})$
, satisfying
$L(1,\eta _{v}\xi _{v})$
, satisfying
for all
![]() $\xi _{v}\in \mathscr {Y}_{v}(\mathbf {C})$
whose underlying scheme point is not a pole.
$\xi _{v}\in \mathscr {Y}_{v}(\mathbf {C})$
whose underlying scheme point is not a pole.
Proof Part 1 is proved as in [Reference DisegniDis17, Lemma 3.3.1], except that we write the arbitrary
![]() $\phi _{2,v}=c\phi _{2, v}^{\circ }+\phi _{2,v}'$
without the extra factor of equation (3.3.2) ibid. Then the argument shows that (only) when
$\phi _{2,v}=c\phi _{2, v}^{\circ }+\phi _{2,v}'$
without the extra factor of equation (3.3.2) ibid. Then the argument shows that (only) when
![]() $\phi ^{\prime }_{2,v}\neq 0$
, there may be a pole controlled by
$\phi ^{\prime }_{2,v}\neq 0$
, there may be a pole controlled by
![]() $L(1, \eta _{v}\xi _{v})$
.
$L(1, \eta _{v}\xi _{v})$
.
3.4 Theta-Eisenstein family
Fix a compact open subgroup
![]() $U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
(which will be usually omitted from all the notation), and let
$U^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
(which will be usually omitted from all the notation), and let
![]() $U_{F}^{p}:= U^{p} \cap \mathbf {A}^{p\infty , \times }$
. Let
$U_{F}^{p}:= U^{p} \cap \mathbf {A}^{p\infty , \times }$
. Let
![]() $\phi ^{p\infty }\in \mathcal {S}(\mathbf {V}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
be a Schwartz function fixed by
$\phi ^{p\infty }\in \mathcal {S}(\mathbf {V}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
be a Schwartz function fixed by
![]() $U^{p}$
. Let
$U^{p}$
. Let
![]() $\xi \colon F^{\times }\backslash \mathbf {A}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character fixed by
$\xi \colon F^{\times }\backslash \mathbf {A}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character fixed by
![]() $U_{F}^{p}$
such that
$U_{F}^{p}$
such that
![]() $\xi (x_{\infty })=x_{\infty }^{k_{0}}$
for some
$\xi (x_{\infty })=x_{\infty }^{k_{0}}$
for some
![]() $k_{0}\in \mathbf {Z}$
, and let
$k_{0}\in \mathbf {Z}$
, and let
![]() $k\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
satisfy
$k\in \mathbf {Z}_{\geq 0}^{\Sigma _{\infty }}$
satisfy
![]() $k_{v}+k_{0}\geq 0 $
for all v.
$k_{v}+k_{0}\geq 0 $
for all v.
We fix a choice of a Schwartz function in
![]() $\mathcal {S}(\mathbf {V}_{2, p}\times F_{p}^{\times })$
as follows. Let
$\mathcal {S}(\mathbf {V}_{2, p}\times F_{p}^{\times })$
as follows. Let
![]() $U_{F, p}^{\circ }\subset \mathscr {O}_{F,p}^{\times }$
be as fixed in Section 2.4.5. For
$U_{F, p}^{\circ }\subset \mathscr {O}_{F,p}^{\times }$
be as fixed in Section 2.4.5. For
![]() $r\in \mathbf {Z}_{\geq 1}^{S_{p}}$
and
$r\in \mathbf {Z}_{\geq 1}^{S_{p}}$
and
![]() $\kappa _{1}'\colon U_{F, p}^{\circ } \to \mathbf {C}^{\times }$
a smooth character, we define
$\kappa _{1}'\colon U_{F, p}^{\circ } \to \mathbf {C}^{\times }$
a smooth character, we define
 $$ \begin{align}\begin{aligned} \phi_{1, r, \kappa_{1}', p}(x_{1}, u)&=\delta_{1, r, p}(x) \mathbf{1}_{U_{F, p}^{\circ}} \kappa_{1}' (u):= \prod_{v\vert p} \phi_{1, r_{v}, \kappa_{1}', v}(x_{1,v}, u_{v}), \\ \phi_{1, r_{v}, \kappa_{1}', v}(x_{1,v}, u_{v}) &:={ \mathrm{vol}(\mathscr{O}_{E, v}, dt)\over \mathrm{vol}(1+\varpi_{v}^{r_{v}}\mathscr{O}_{E,v}, d^{\times}t)} \mathbf{1}_{1+\varpi_{v}^{r_{v}}\mathscr{O}_{E,v}}(x_{1,v}) \mathbf{1}_{U_{F, p}^{\circ}}(u)\kappa_{1}'(u), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \phi_{1, r, \kappa_{1}', p}(x_{1}, u)&=\delta_{1, r, p}(x) \mathbf{1}_{U_{F, p}^{\circ}} \kappa_{1}' (u):= \prod_{v\vert p} \phi_{1, r_{v}, \kappa_{1}', v}(x_{1,v}, u_{v}), \\ \phi_{1, r_{v}, \kappa_{1}', v}(x_{1,v}, u_{v}) &:={ \mathrm{vol}(\mathscr{O}_{E, v}, dt)\over \mathrm{vol}(1+\varpi_{v}^{r_{v}}\mathscr{O}_{E,v}, d^{\times}t)} \mathbf{1}_{1+\varpi_{v}^{r_{v}}\mathscr{O}_{E,v}}(x_{1,v}) \mathbf{1}_{U_{F, p}^{\circ}}(u)\kappa_{1}'(u), \end{aligned}\end{align} $$
which is invariant under
![]() $N(\mathscr {O}_{F,p})=\prod _{v\vert p} N(\mathscr {O}_{F,v})$
.
$N(\mathscr {O}_{F,p})=\prod _{v\vert p} N(\mathscr {O}_{F,v})$
.
Let
![]() $\kappa _{2}'\colon U_{F, p}^{\circ }\to \mathbf {C}^{\times }$
be a smooth character. For
$\kappa _{2}'\colon U_{F, p}^{\circ }\to \mathbf {C}^{\times }$
be a smooth character. For
![]() $t\in \mathbf {A}_{E}^{\times }$
,
$t\in \mathbf {A}_{E}^{\times }$
,
![]() $r\geq \underline {1}$
, and
$r\geq \underline {1}$
, and
![]() $\phi ^{p\infty }=\phi _{1}^{p\infty }\otimes \phi _{2}^{p\infty }\in \mathcal {S}(\mathbf {V}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
, define a form in
$\phi ^{p\infty }=\phi _{1}^{p\infty }\otimes \phi _{2}^{p\infty }\in \mathcal {S}(\mathbf {V}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
, define a form in
![]() $N_{(l_{0}-k_{0}, {2}+ l + k_{0}+2k)}^{\leq k}(\mathbf {C})$
by
$N_{(l_{0}-k_{0}, {2}+ l + k_{0}+2k)}^{\leq k}(\mathbf {C})$
by
where the product
![]() $\star $
is (2.2.7), and
$\star $
is (2.2.7), and
![]() $E_{r}(\cdot )=(3.3.12)$
.
$E_{r}(\cdot )=(3.3.12)$
.
Fix a compact open subgroup
![]() $U_{\mathrm {H}}^{p}\subset \mathbf {A}_{E}^{p\infty , \times }$
(which will be omitted from all the notation). Let
$U_{\mathrm {H}}^{p}\subset \mathbf {A}_{E}^{p\infty , \times }$
(which will be omitted from all the notation). Let
![]() $\underline {l}$
be a complex weight for
$\underline {l}$
be a complex weight for
![]() $\mathrm {H}$
, let
$\mathrm {H}$
, let
![]() $\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character of weight
$\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\times }\to \mathbf {C}^{\times }$
be a locally algebraic character of weight
![]() $\underline {l}$
fixed by
$\underline {l}$
fixed by
![]() $U_{\mathrm {H}}^{p}$
, and assume that for all
$U_{\mathrm {H}}^{p}$
, and assume that for all
![]() $w\vert v\vert p$
, the integer
$w\vert v\vert p$
, the integer
![]() $r_{v}\geq 1$
is greater than the conductors of
$r_{v}\geq 1$
is greater than the conductors of
![]() $\chi _{w}$
,
$\chi _{w}$
,
![]() $\xi _{v}$
,
$\xi _{v}$
,
![]() $\kappa _{2,v}'$
. Then we define
$\kappa _{2,v}'$
. Then we define
which does not depend on the choice of r; here,
![]() $\kappa _{1,\chi , p}'$
is as in (2.4.3), namely
$\kappa _{1,\chi , p}'$
is as in (2.4.3), namely
for
![]() $j'\colon U_{F, p}^{\circ }\to \mathscr {O}_{E, p}^{\times }$
as in (2.4.7).
$j'\colon U_{F, p}^{\circ }\to \mathscr {O}_{E, p}^{\times }$
as in (2.4.7).
Lemma 3.11 For each
![]() $c\in \mathbf {A}^{+}$
satisfying
$c\in \mathbf {A}^{+}$
satisfying
![]() $v(c)\geq 1$
for some
$v(c)\geq 1$
for some
![]() $v\vert p$
, the c
th Whittaker–Fourier coefficient of
$v\vert p$
, the c
th Whittaker–Fourier coefficient of
![]() $ I(\phi ^{p\infty }; \chi , \xi ,\kappa _{2}', k) $
is
$ I(\phi ^{p\infty }; \chi , \xi ,\kappa _{2}', k) $
is
 $$ \begin{align*} &W_{ I}^{\mathbf{C}}(c) = {-\varepsilon(\mathbf{V}_{2})\cdot 2^{[F:\mathbf{Q}]} \over L^{(p)}(1, \eta)} {|D_{E/F}|^{1/2}\over |D_{F}|^{1/2}} \cdot \sum_{a/c\in F, \ 0<a/c<1} \chi^{\infty}(a) a_{\infty}^{(| l | +l_{0})/2} \xi^{\infty, -1}(c-a)(a-c)_{\infty}^{k} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \prod_{v\nmid p\infty} J_{v}(a, c, \phi_{v}; \chi_{v}, \xi_{v}) \prod_{v\vert p} J_{v}(a, c; \chi_{v}, \xi_{v}, \kappa_{2,v}'). \end{align*} $$
$$ \begin{align*} &W_{ I}^{\mathbf{C}}(c) = {-\varepsilon(\mathbf{V}_{2})\cdot 2^{[F:\mathbf{Q}]} \over L^{(p)}(1, \eta)} {|D_{E/F}|^{1/2}\over |D_{F}|^{1/2}} \cdot \sum_{a/c\in F, \ 0<a/c<1} \chi^{\infty}(a) a_{\infty}^{(| l | +l_{0})/2} \xi^{\infty, -1}(c-a)(a-c)_{\infty}^{k} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad \prod_{v\nmid p\infty} J_{v}(a, c, \phi_{v}; \chi_{v}, \xi_{v}) \prod_{v\vert p} J_{v}(a, c; \chi_{v}, \xi_{v}, \kappa_{2,v}'). \end{align*} $$
Here, taking
![]() $\phi _{1, v} = \phi _{1, r_{v},\kappa _{1,\chi ,v}'}$
with
$\phi _{1, v} = \phi _{1, r_{v},\kappa _{1,\chi ,v}'}$
with
![]() $ \kappa _{1,\chi ,v}':= \chi _{v}\circ j_{v}$
and
$ \kappa _{1,\chi ,v}':= \chi _{v}\circ j_{v}$
and
![]() $\phi _{2,v}=\phi _{2, \kappa _{2,v}'}$
if
$\phi _{2,v}=\phi _{2, \kappa _{2,v}'}$
if
![]() $v\vert p$
, we define, for all
$v\vert p$
, we define, for all
![]() $v\nmid p\infty $
,
$v\nmid p\infty $
,
 $$ \begin{align}\begin{aligned} \qquad\quad & J_{v}(a, c, (\phi_{v});\chi_{v},\xi_{v}, (\kappa_{2, v}'))\\ & \quad := \int_{E_{v}^{\times}} \chi_{v}(t) r_{1}(t)\phi_{1, v}(1, a) W^{\circ}_{c-q(t) a, v}(1, q(t)a, (\phi_{2,v}); \xi, (\kappa_{2,v}')) \, d^{\bullet}t_{v}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \qquad\quad & J_{v}(a, c, (\phi_{v});\chi_{v},\xi_{v}, (\kappa_{2, v}'))\\ & \quad := \int_{E_{v}^{\times}} \chi_{v}(t) r_{1}(t)\phi_{1, v}(1, a) W^{\circ}_{c-q(t) a, v}(1, q(t)a, (\phi_{2,v}); \xi, (\kappa_{2,v}')) \, d^{\bullet}t_{v}, \end{aligned}\end{align} $$
for the measure
![]() $d^{\bullet }t_{v}$
giving volume
$d^{\bullet }t_{v}$
giving volume
![]() $1$
to
$1$
to
![]() $\mathscr {O}_{E, v}^{\times }$
.
$\mathscr {O}_{E, v}^{\times }$
.
Proof We lighten some of the notation. The assumptions of Lemma 3.2 are satisfied; therefore, for
![]() $c\in F^{+}$
and
$c\in F^{+}$
and
![]() $g=\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right ) $
with
$g=\left (\begin {smallmatrix}y&x\\&1\end {smallmatrix}\right ) $
with
![]() $y\in \mathbf {A} ^{+}$
and
$y\in \mathbf {A} ^{+}$
and
![]() $x\in \mathbf {A}$
,
$x\in \mathbf {A}$
,
 $$ \begin{align*} & I(g; \chi, \xi,\kappa_{2}', k)\\&\quad = {|D_{E/F}|^{1/2}\over |D_{F}|^{1/2}} \eta(y) |y|^{1/2} y_{\infty}^{ | l |+l_{0}\over 2} \sum_{a\in F^{+}} \int_{{\mathbf{A}}_{E}^{\infty,\times} } \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(y,y^{-1} a) \ {E}(g,q(t) a) \, d^{\bullet}t\, \mathbf{q}^{a} \\ &\quad= {|D_{E/F}|^{1/2} \over |D_{F}|^{1/2}} |y|^{1/2} \eta\chi(y) y_{\infty}^{( | l | -l_{0})/2} \sum_{a\in F^{+}} \int_{{\mathbf{A}}_{E}^{\infty,\times} } \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(1, ay) \ {E}(g,q(t)ay^{2}) \, d^{\bullet}t\, \mathbf{q}^{a}\!. \\ \end{align*} $$
$$ \begin{align*} & I(g; \chi, \xi,\kappa_{2}', k)\\&\quad = {|D_{E/F}|^{1/2}\over |D_{F}|^{1/2}} \eta(y) |y|^{1/2} y_{\infty}^{ | l |+l_{0}\over 2} \sum_{a\in F^{+}} \int_{{\mathbf{A}}_{E}^{\infty,\times} } \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(y,y^{-1} a) \ {E}(g,q(t) a) \, d^{\bullet}t\, \mathbf{q}^{a} \\ &\quad= {|D_{E/F}|^{1/2} \over |D_{F}|^{1/2}} |y|^{1/2} \eta\chi(y) y_{\infty}^{( | l | -l_{0})/2} \sum_{a\in F^{+}} \int_{{\mathbf{A}}_{E}^{\infty,\times} } \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(1, ay) \ {E}(g,q(t)ay^{2}) \, d^{\bullet}t\, \mathbf{q}^{a}\!. \\ \end{align*} $$
Now, for
![]() $\lambda = {-\varepsilon (\mathbf {V}_{2})/ L^{(p)}(1, \eta )}$
, by Corollary 3.9, we have
$\lambda = {-\varepsilon (\mathbf {V}_{2})/ L^{(p)}(1, \eta )}$
, by Corollary 3.9, we have
 $$ \begin{align*}&{E}(g,q(t) ay^{2})= \lambda \cdot |y|^{1/2} \eta\xi^{-1}(y) \\&\quad\times\left(W_{0}(y, u) + (-1)_{\infty}^{k}\sum_{b\in F^{+}} 2^{[F:\mathbf{Q}]} (by_{\infty})^{k+k_{0}} Q_{k_{0}, \underline{k}} ((4\pi b y_{\infty})^{-1}) W^{\circ, \infty}_{by}(1, q(t)ay, \xi) \,\mathbf{q}^{b}\right)\end{align*} $$
$$ \begin{align*}&{E}(g,q(t) ay^{2})= \lambda \cdot |y|^{1/2} \eta\xi^{-1}(y) \\&\quad\times\left(W_{0}(y, u) + (-1)_{\infty}^{k}\sum_{b\in F^{+}} 2^{[F:\mathbf{Q}]} (by_{\infty})^{k+k_{0}} Q_{k_{0}, \underline{k}} ((4\pi b y_{\infty})^{-1}) W^{\circ, \infty}_{by}(1, q(t)ay, \xi) \,\mathbf{q}^{b}\right)\end{align*} $$
so that
for some coefficients
![]() $W_{I, c}^{\mathbf {C}}(y)$
, which we now explicitly calculate if c satisfies
$W_{I, c}^{\mathbf {C}}(y)$
, which we now explicitly calculate if c satisfies
![]() $v(c)\geq 1$
for some
$v(c)\geq 1$
for some
![]() $v\vert p$
. Under this condition, we have
$v\vert p$
. Under this condition, we have
 $$ \begin{align*} &W_{I, c}^{\mathbf{C}}(y)= {-\varepsilon(\mathbf{V}_{2})\cdot 2^{[F:\mathbf{Q}]}\over L^{(p)}(1, \eta)} {|D_{E/F}|^{1/2}\over |D_{F}|^{1/2}} \sum_{\substack{a\in F^{}\\ 0<a<c }} (ay)_{\infty}^{(| l |-l_{0})/2} \int_{{\mathbf{A}}_{E}^{\infty,\times}} \chi(ay) \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(1, ay)\\ &\cdot (-1)_{\infty}^{k} \xi^{-1}((c-a)y) ((c-a)y_{\infty})^{k+k_{0}} W^{\circ, \infty}_{(c-q(t) a)y}(1, q(t)ay, \xi) Q_{k_{0}, \underline{k}} ((4\pi (c-a) y_{\infty})^{-1}) \, dt, \end{align*} $$
$$ \begin{align*} &W_{I, c}^{\mathbf{C}}(y)= {-\varepsilon(\mathbf{V}_{2})\cdot 2^{[F:\mathbf{Q}]}\over L^{(p)}(1, \eta)} {|D_{E/F}|^{1/2}\over |D_{F}|^{1/2}} \sum_{\substack{a\in F^{}\\ 0<a<c }} (ay)_{\infty}^{(| l |-l_{0})/2} \int_{{\mathbf{A}}_{E}^{\infty,\times}} \chi(ay) \chi^{\infty}(t) r_{1}(t)\phi_{1}^{\infty}(1, ay)\\ &\cdot (-1)_{\infty}^{k} \xi^{-1}((c-a)y) ((c-a)y_{\infty})^{k+k_{0}} W^{\circ, \infty}_{(c-q(t) a)y}(1, q(t)ay, \xi) Q_{k_{0}, \underline{k}} ((4\pi (c-a) y_{\infty})^{-1}) \, dt, \end{align*} $$
where we have noted that, since we have assumed
![]() $v(c)\geq 1$
and the choice of
$v(c)\geq 1$
and the choice of
![]() $\phi _{1, p}$
implies
$\phi _{1, p}$
implies
![]() $v(a)=0$
, the constant term (corresponding to
$v(a)=0$
, the constant term (corresponding to
![]() $a=c$
) of the Eisenstein series does not contribute. Finally, we rewrite the resulting formula with c in place of
$a=c$
) of the Eisenstein series does not contribute. Finally, we rewrite the resulting formula with c in place of
![]() $cy$
.
$cy$
.
Lemma 3.12 Let
![]() $a, c\in \mathbf {A}^{\infty , \times }$
, let
$a, c\in \mathbf {A}^{\infty , \times }$
, let
![]() $\phi _{2}^{p\infty } \in \mathcal {S}(\mathbf {V}_{2}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
, and let
$\phi _{2}^{p\infty } \in \mathcal {S}(\mathbf {V}_{2}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
, and let
![]() $\xi \colon F^{\times }\backslash \mathbf {A}^{\times }\to \mathbf {C}^{\times }$
,
$\xi \colon F^{\times }\backslash \mathbf {A}^{\times }\to \mathbf {C}^{\times }$
,
![]() $\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\times } \to \mathbf {C}^{\times }$
be locally algebraic characters.
$\chi \colon E^{\times }\backslash \mathbf {A}_{E}^{\times } \to \mathbf {C}^{\times }$
be locally algebraic characters.
-
(1) For
 $v\vert p$
, if
$v\vert p$
, if
 $v(c)\geq 1$
, then
$v(c)\geq 1$
, then  $$ \begin{align*}|d_{v}|^{-3/2} |D_{v}|^{-1/2}\cdot J_{v}(a, c; \chi_{v}, \xi_{v}, \kappa_{2,v}') = \xi_{v}(-1) \mathbf{1}_{U_{F,v}^{\circ}}(a_{v}) \kappa_{1, \chi, v}'\kappa_{2, v}'(a_{v}). \end{align*} $$
$$ \begin{align*}|d_{v}|^{-3/2} |D_{v}|^{-1/2}\cdot J_{v}(a, c; \chi_{v}, \xi_{v}, \kappa_{2,v}') = \xi_{v}(-1) \mathbf{1}_{U_{F,v}^{\circ}}(a_{v}) \kappa_{1, \chi, v}'\kappa_{2, v}'(a_{v}). \end{align*} $$
-
(2) For all but finitely many
 $v\nmid p$
,
$v\nmid p$
,  $$ \begin{align*}|d_{v}|^{-3/2} |D_{v}|^{-1/2} J_{v}(a, c, \phi_{v}; \chi_{v}, \xi_{v}) =1.\end{align*} $$
$$ \begin{align*}|d_{v}|^{-3/2} |D_{v}|^{-1/2} J_{v}(a, c, \phi_{v}; \chi_{v}, \xi_{v}) =1.\end{align*} $$
-
(3) For all
 $v\nmid p\infty $
, there is a function
$v\nmid p\infty $
, there is a function
 $\mathbf {J}_{v}(a, c, , \phi _{v})\in \mathscr {O}(\mathscr {Y}_{\mathrm {H}, v}\times \mathscr {Y}_{v})$
such that for all
$\mathbf {J}_{v}(a, c, , \phi _{v})\in \mathscr {O}(\mathscr {Y}_{\mathrm {H}, v}\times \mathscr {Y}_{v})$
such that for all
 $(\chi _{v}, \xi _{v})\in \mathscr {Y}_{\mathrm {H}, v}\times \mathscr {Y}_{v}(\mathbf {C})$
,
$(\chi _{v}, \xi _{v})\in \mathscr {Y}_{\mathrm {H}, v}\times \mathscr {Y}_{v}(\mathbf {C})$
,  $$ \begin{align*}\mathbf{J}_{v}(a, c, \phi_{v})(\chi_{v}, \xi_{v})= |d_{v}|^{-3/2} |D_{v}|^{-1/2} J_{v}(a, c, \phi_{v}; \chi_{v}, \xi_{v}).\end{align*} $$
$$ \begin{align*}\mathbf{J}_{v}(a, c, \phi_{v})(\chi_{v}, \xi_{v})= |d_{v}|^{-3/2} |D_{v}|^{-1/2} J_{v}(a, c, \phi_{v}; \chi_{v}, \xi_{v}).\end{align*} $$
Proof Part 1 follows from the definitions and Proposition 3.8.3. Part 2 follows from Proposition 3.8.2 and a simple calculation. Finally, since the integrand in (3.4.4) is compactly supported, part 3 follows from Proposition 3.10.
Let
 $$ \begin{align}\begin{aligned} \lambda:= {-\varepsilon(\mathbf{V}_{2}) \cdot 2^{[F:\mathbf{Q}]}\over |D_{E/F}|^{1/2} L^{(p)}(1, \eta)} \in\mathbf{Q}^{\times}.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \lambda:= {-\varepsilon(\mathbf{V}_{2}) \cdot 2^{[F:\mathbf{Q}]}\over |D_{E/F}|^{1/2} L^{(p)}(1, \eta)} \in\mathbf{Q}^{\times}.\end{aligned}\end{align} $$
For the sake of simplicity, we momentarily introduce the assumption that the weight
![]() $\underline {l}$
of
$\underline {l}$
of
![]() $\chi $
satisfies
$\chi $
satisfies
![]() $l \geq 0$
. We will see in Corollary 3.15 that this does not affect our main construction.
$l \geq 0$
. We will see in Corollary 3.15 that this does not affect our main construction.
Proposition 3.13 Let
![]() $\chi \in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}$
have weight
$\chi \in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}$
have weight
![]() $\underline {\kappa }_{1}=\underline {\kappa }_{\mathrm {H}}(\chi )$
, and let
$\underline {\kappa }_{1}=\underline {\kappa }_{\mathrm {H}}(\chi )$
, and let
![]() $\underline {\kappa }_{2}=(\kappa _{2,0}, \kappa _{2})\in \frak W^{\mathrm {cl}}$
. Let
$\underline {\kappa }_{2}=(\kappa _{2,0}, \kappa _{2})\in \frak W^{\mathrm {cl}}$
. Let
![]() $U_{F}^{\circ }:= U_{F}^{p}U_{F, p}^{\circ }$
. Write
$U_{F}^{\circ }:= U_{F}^{p}U_{F, p}^{\circ }$
. Write
![]() $\xi =\kappa _{2, 0}^{-1}$
and
$\xi =\kappa _{2, 0}^{-1}$
and
 $$ \begin{align}\begin{aligned} {}&\kappa_{1, 0, p}=\kappa_{1,0, p}^{\mathrm{sm}} (\cdot )^{l_{0}}, \qquad &\kappa_{2, 0, p}= \kappa_{2, 0, p}^{\mathrm{sm}}(\cdot )^{-k_{0}}, \\ {}&\kappa_{1}=\kappa_{1}^{\mathrm{sm}}(\cdot )^{(l+l_{0})/ 2}, \qquad &\kappa_{2}=\kappa_{2}^{\mathrm{sm}} (\cdot)^{k}.\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} {}&\kappa_{1, 0, p}=\kappa_{1,0, p}^{\mathrm{sm}} (\cdot )^{l_{0}}, \qquad &\kappa_{2, 0, p}= \kappa_{2, 0, p}^{\mathrm{sm}}(\cdot )^{-k_{0}}, \\ {}&\kappa_{1}=\kappa_{1}^{\mathrm{sm}}(\cdot )^{(l+l_{0})/ 2}, \qquad &\kappa_{2}=\kappa_{2}^{\mathrm{sm}} (\cdot)^{k}.\end{aligned}\end{align} $$
Assume that
![]() $l_{\tau }, k_{\tau }, k_{\tau }+k_{0}\geq 0$
for all
$l_{\tau }, k_{\tau }, k_{\tau }+k_{0}\geq 0$
for all
![]() $\tau \in \Sigma _{p}$
. Let
$\tau \in \Sigma _{p}$
. Let
be as in (2.4.3). Let
![]() $n\in \mathbf {N}$
be sufficiently large (depending on
$n\in \mathbf {N}$
be sufficiently large (depending on
![]() $\xi , \chi $
). The coefficients
$\xi , \chi $
). The coefficients
 $$ \begin{align} W_{(\mathrm{U}^{\circ})_{p}^{n!}\, \mathrm{I}(\phi^{p\infty})}(c)(\chi, \underline{\kappa}_{2}) &:= \lambda \cdot \sum_{\substack{a/c\in F \\ 0<a/c< p^{n!}}} \mathbf{1}_{U_{F, p}^{\circ}}(a_{p}) \kappa_{1}(a_{p})\kappa_{2}((a-p^{n!}c)_{p}) \nonumber\\ &\quad\cdot\kappa_{1,0}^{p\infty}(a)\kappa_{2, 0}^{p\infty}(-a) \prod_{v\nmid p} \mathbf{J}_{v}(a, c, \phi_{v}; \xi_{v}, \chi_{v}), \end{align} $$
$$ \begin{align} W_{(\mathrm{U}^{\circ})_{p}^{n!}\, \mathrm{I}(\phi^{p\infty})}(c)(\chi, \underline{\kappa}_{2}) &:= \lambda \cdot \sum_{\substack{a/c\in F \\ 0<a/c< p^{n!}}} \mathbf{1}_{U_{F, p}^{\circ}}(a_{p}) \kappa_{1}(a_{p})\kappa_{2}((a-p^{n!}c)_{p}) \nonumber\\ &\quad\cdot\kappa_{1,0}^{p\infty}(a)\kappa_{2, 0}^{p\infty}(-a) \prod_{v\nmid p} \mathbf{J}_{v}(a, c, \phi_{v}; \xi_{v}, \chi_{v}), \end{align} $$
for
![]() $c\in \mathbf {A}^{+}$
with
$c\in \mathbf {A}^{+}$
with
![]() $v(c)\geq 0$
for all
$v(c)\geq 0$
for all
![]() $v\vert p$
, define a p-adic modular form
$v\vert p$
, define a p-adic modular form
such that for every
![]() $\iota \colon \mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})\hookrightarrow \mathbf {C}$
, we have
$\iota \colon \mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})\hookrightarrow \mathbf {C}$
, we have
Moreover, if
![]() $\phi _{2}^{p\infty }$
satisfies (
3.3.7
), then
$\phi _{2}^{p\infty }$
satisfies (
3.3.7
), then
Proof From Lemmas 3.11 and 3.12, we find an expression which can be brought into the above form, after replacing
![]() $p^{n!}c$
with c whenever it occurs as the argument of a smooth function.
$p^{n!}c$
with c whenever it occurs as the argument of a smooth function.
The second assertion follows from (2.3.6), Corollary 3.7, and (3.3.13).
With notation as in Proposition 3.13, let
It is easy to verify, using only that
![]() $\mathbf {J}^{p}(\cdot )$
is a Schwartz function of
$\mathbf {J}^{p}(\cdot )$
is a Schwartz function of
![]() $a\in \mathbf {A}^{p\infty , \times }$
, that the Riemann sums
$a\in \mathbf {A}^{p\infty , \times }$
, that the Riemann sums
for
![]() $\varphi \colon U_{F, p}^{\circ }\to \mathbf {Q}_{p}(\kappa _{2}, \xi )$
locally constant, converge to a measure (bounded distribution)
$\varphi \colon U_{F, p}^{\circ }\to \mathbf {Q}_{p}(\kappa _{2}, \xi )$
locally constant, converge to a measure (bounded distribution)
on
![]() $U_{F, p}^{\circ }$
valued in
$U_{F, p}^{\circ }$
valued in
![]() $\mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})$
. Then, by the same argument of the standard result in [Reference KoblitzKob77, Theorem 6 on p. 39], any continuous
$\mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})$
. Then, by the same argument of the standard result in [Reference KoblitzKob77, Theorem 6 on p. 39], any continuous
![]() $\mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})$
-valued function is integrable for this measure. The same holds with
$\mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})$
-valued function is integrable for this measure. The same holds with
![]() $\mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})$
replaced by
$\mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})$
replaced by
![]() $\mathscr {O}(\mathscr {Y}_{\mathrm {H}}\hat {\times } \frak W)$
and
$\mathscr {O}(\mathscr {Y}_{\mathrm {H}}\hat {\times } \frak W)$
and
![]() $\chi , \underline {\kappa }_{2}$
by the universal characters,
$\chi , \underline {\kappa }_{2}$
by the universal characters,
![]() $\mathbf {J}^{p}$
by the universal function; for this universal situation, we will use the same notation without
$\mathbf {J}^{p}$
by the universal function; for this universal situation, we will use the same notation without
![]() $\chi , \underline {\kappa }_{2}$
.
$\chi , \underline {\kappa }_{2}$
.
Corollary 3.14 Let
![]() ${S}^{\mathrm {bad}}$
be the set of places of F at which
${S}^{\mathrm {bad}}$
be the set of places of F at which
![]() $\phi ^{p\infty }$
is not the standard Schwartz function. Denote
$\phi ^{p\infty }$
is not the standard Schwartz function. Denote
![]() $\underline {\kappa }_{1}=\underline {\kappa }_{\mathrm {H}}(\chi _{\mathrm {univ}})$
. Assume that
$\underline {\kappa }_{1}=\underline {\kappa }_{\mathrm {H}}(\chi _{\mathrm {univ}})$
. Assume that
![]() $\phi _{2}^{p\infty }$
satisfies (
3.3.7
). The sequence of coefficients
$\phi _{2}^{p\infty }$
satisfies (
3.3.7
). The sequence of coefficients

has poles controlled by
![]() $\prod _{v\in S^{\mathrm {bad}}}L(1, \eta _{v}\kappa _{2, 0,v}^{-1})$
. It defines an ordinary meromorphic
$\prod _{v\in S^{\mathrm {bad}}}L(1, \eta _{v}\kappa _{2, 0,v}^{-1})$
. It defines an ordinary meromorphic
![]() $\mathscr {Y}_{\mathrm {H}}\hat {\times }\frak W$
-adic modular form (Section 2.4.4)
$\mathscr {Y}_{\mathrm {H}}\hat {\times }\frak W$
-adic modular form (Section 2.4.4)
of weight
![]() $\underline {\kappa }_{1}\underline {\kappa }_{2}$
, which satisfies the following property.
$\underline {\kappa }_{1}\underline {\kappa }_{2}$
, which satisfies the following property.
For all
![]() $\chi \in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}(\mathbf {C})$
,
$\chi \in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}(\mathbf {C})$
,
![]() $\underline {\kappa }_{2}\in \frak W^{\mathrm {cl}}(\mathbf {C})$
with underlying numerical weights
$\underline {\kappa }_{2}\in \frak W^{\mathrm {cl}}(\mathbf {C})$
with underlying numerical weights
![]() $\underline {l}$
,
$\underline {l}$
,
![]() $\underline {k}$
such that
$\underline {k}$
such that
![]() $l_{\tau }, k_{\tau }, k_{\tau }+k_{0}\geq 0$
for all
$l_{\tau }, k_{\tau }, k_{\tau }+k_{0}\geq 0$
for all
![]() $\tau $
, we have
$\tau $
, we have
where
![]() $\iota \colon \mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})\hookrightarrow \mathbf {C}$
is the embedding attached to the complex geometric point
$\iota \colon \mathbf {Q}_{p}(\chi , \underline {\kappa }_{2})\hookrightarrow \mathbf {C}$
is the embedding attached to the complex geometric point
![]() $(\chi , \underline {\kappa }_{2})$
.
$(\chi , \underline {\kappa }_{2})$
.
Proof The interpolation property (3.4.9) at the level of q-expansions follows from Proposition 3.13 and the previous discussion. The simplification in the argument of
![]() $\kappa _{2}$
in the interpolated coefficient (3.4.7) is justified by the fact that
$\kappa _{2}$
in the interpolated coefficient (3.4.7) is justified by the fact that
![]() $\kappa _{2}(a-p^{n!}c)-\kappa _{2}(a)\to 0$
uniformly in a, and that the expression of interest is a bounded function of
$\kappa _{2}(a-p^{n!}c)-\kappa _{2}(a)\to 0$
uniformly in a, and that the expression of interest is a bounded function of
![]() $\kappa _{2}(\cdot )$
. Lemma 2.4.4 then shows the existence of the
$\kappa _{2}(\cdot )$
. Lemma 2.4.4 then shows the existence of the
![]() $\mathscr {Y}_{\mathrm {H}}\hat {\times }\frak W$
-adic modular form
$\mathscr {Y}_{\mathrm {H}}\hat {\times }\frak W$
-adic modular form
![]() $\mathbf { I}^{\mathrm {ord}}(\phi ^{p\infty };\chi , \underline {\kappa }_{2})$
.
$\mathbf { I}^{\mathrm {ord}}(\phi ^{p\infty };\chi , \underline {\kappa }_{2})$
.
Consider the weight map
 $$ \begin{align*}\begin{aligned} \varphi\colon (\mathscr{Y}_{\mathrm{G}}\hat{\times} \mathscr{Y}_{\mathrm{H}})&\to \frak W\\ (x, y)&\mapsto \underline{\kappa}_{x}. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \varphi\colon (\mathscr{Y}_{\mathrm{G}}\hat{\times} \mathscr{Y}_{\mathrm{H}})&\to \frak W\\ (x, y)&\mapsto \underline{\kappa}_{x}. \end{aligned}\end{align*} $$
Recycling notation (in a way that should cause no confusion), define an ordinary meromorphic
![]() $(\mathscr {Y}_{\mathrm {G}}\hat {\times } \mathscr {Y}_{\mathrm {H}})$
-adic modular cuspform of weight
$(\mathscr {Y}_{\mathrm {G}}\hat {\times } \mathscr {Y}_{\mathrm {H}})$
-adic modular cuspform of weight
![]() $\varphi $
by
$\varphi $
by
where the right-hand side is the form of Corollary 3.14. We denote by
the pullback of
![]() $\mathbf {I}^{\mathrm {ord}}(\phi ^{p\infty },x, y)$
under the involution
$\mathbf {I}^{\mathrm {ord}}(\phi ^{p\infty },x, y)$
under the involution
![]() $\mathscr {Y}_{\mathrm {G}}\times \mathscr {Y}_{\mathrm {H}}\stackrel {\curlyvee \times \mathrm {id}}{\longrightarrow } \mathscr {Y}_{\mathrm {G}}\times \mathscr {Y}_{\mathrm {H}}$
.
$\mathscr {Y}_{\mathrm {G}}\times \mathscr {Y}_{\mathrm {H}}\stackrel {\curlyvee \times \mathrm {id}}{\longrightarrow } \mathscr {Y}_{\mathrm {G}}\times \mathscr {Y}_{\mathrm {H}}$
.
Corollary 3.15 Assume that
![]() $\phi _{2}^{p\infty }$
satisfies (3.3.7). For all
$\phi _{2}^{p\infty }$
satisfies (3.3.7). For all
![]() $x\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C})$
and
$x\in \mathscr {Y}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C})$
and
![]() $y \in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}(\mathbf {C})$
, of weights
$y \in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}(\mathbf {C})$
, of weights
![]() $\underline {w}$
,
$\underline {w}$
,
![]() $\underline {l}$
such that for all
$\underline {l}$
such that for all
![]() $\tau \in \Sigma _{\infty }$
,
$\tau \in \Sigma _{\infty }$
,
we have
where:
-
•
 $\xi =\xi _{x,y} = \omega _{{x}} \omega _{y}$
, whose weight we denote by
$\xi =\xi _{x,y} = \omega _{{x}} \omega _{y}$
, whose weight we denote by
 $k_{0}$
;
$k_{0}$
; -
•
 $k_{x,y} = (w- 2 - | l | - k_{0}) /2 $
;
$k_{x,y} = (w- 2 - | l | - k_{0}) /2 $
; -
•
 $\kappa _{2,x,y}' = \kappa _{{x}}^{\curlyvee }{}^{\prime } \cdot \kappa _{y}^{\prime -1}$
(with notation as in (
2.4.3
));
$\kappa _{2,x,y}' = \kappa _{{x}}^{\curlyvee }{}^{\prime } \cdot \kappa _{y}^{\prime -1}$
(with notation as in (
2.4.3
)); -
•
 $\iota \colon \mathbf {Q}_{p}(x, y)\hookrightarrow \mathbf {C}$
is the embedding attached to the complex geometric point
$\iota \colon \mathbf {Q}_{p}(x, y)\hookrightarrow \mathbf {C}$
is the embedding attached to the complex geometric point
 $(x, y)$
.
$(x, y)$
.
Proof The interpolation property at characters satisfying
![]() $l\geq 0$
follows from Proposition 3.13 via Corollary 3.14; the same argument also goes through without the assumption
$l\geq 0$
follows from Proposition 3.13 via Corollary 3.14; the same argument also goes through without the assumption
![]() $l\geq 0$
, since the weight of the chosen theta-Eisenstein series does not depend on
$l\geq 0$
, since the weight of the chosen theta-Eisenstein series does not depend on
![]() $\underline {l}$
(or y) but only on x. The inequalities on the weights come from the conditions
$\underline {l}$
(or y) but only on x. The inequalities on the weights come from the conditions
![]() $k, k+k_{0}\geq 0$
.
$k, k+k_{0}\geq 0$
.
4 Zeta integrals
In this final section, we interpolate global and local (away from
![]() $p\infty $
) zeta integrals, compute the archimedean and p-adic integrals, and construct the p-adic L-function.
$p\infty $
) zeta integrals, compute the archimedean and p-adic integrals, and construct the p-adic L-function.
As preliminary, we recall gamma factors introduced in the introduction. Let
![]() $F_{v}$
and L be p-adic fields. The (inverse) Deligne–Langlands gamma factor of a potentially semistable representation
$F_{v}$
and L be p-adic fields. The (inverse) Deligne–Langlands gamma factor of a potentially semistable representation
![]() $\rho $
of
$\rho $
of
![]() $\mathrm {Gal}(\overline {F}_{v}/F_{v})$
over L, with respect to a nontrivial character
$\mathrm {Gal}(\overline {F}_{v}/F_{v})$
over L, with respect to a nontrivial character
![]() $\psi _{v}\colon F_{v}\to \mathbf {C}^{\times }$
and an embedding
$\psi _{v}\colon F_{v}\to \mathbf {C}^{\times }$
and an embedding
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, is defined as
$\iota \colon L\hookrightarrow \mathbf {C}$
, is defined as
 $$ \begin{align*}\begin{aligned} \gamma(\iota \rho,\psi_{v})^{-1}:= {L(\iota \mathrm{WD}(\rho))\over \varepsilon(\iota \mathrm{WD}(\rho), \psi_{v}) L(\iota \mathrm{ WD}(\rho^{*}(1)))},\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \gamma(\iota \rho,\psi_{v})^{-1}:= {L(\iota \mathrm{WD}(\rho))\over \varepsilon(\iota \mathrm{WD}(\rho), \psi_{v}) L(\iota \mathrm{ WD}(\rho^{*}(1)))},\end{aligned}\end{align*} $$
where
![]() $\iota \mathrm {WD}$
is Fontaine’s functor [Reference FontaineFon94] to complex Weil–Deligne representations. We also define
$\iota \mathrm {WD}$
is Fontaine’s functor [Reference FontaineFon94] to complex Weil–Deligne representations. We also define
![]() $\gamma (s, W, \psi _{v}):= \gamma (W\otimes |\cdot |^{s}, \psi _{v})$
.
$\gamma (s, W, \psi _{v}):= \gamma (W\otimes |\cdot |^{s}, \psi _{v})$
.
Let
![]() $\mathbf {Q}_{p}^{\mathrm {ab}}$
be the abelian closure of
$\mathbf {Q}_{p}^{\mathrm {ab}}$
be the abelian closure of
![]() $\mathbf {Q}_{p}$
. If
$\mathbf {Q}_{p}$
. If
![]() $W_{\chi }$
is the Weil–Deligne representation corresponding to a smooth character
$W_{\chi }$
is the Weil–Deligne representation corresponding to a smooth character
![]() $\chi \colon F_{v}\to \mathbf {Q}_{p}^{\mathrm {ab, \times }}$
, then for any
$\chi \colon F_{v}\to \mathbf {Q}_{p}^{\mathrm {ab, \times }}$
, then for any
![]() $\sigma \in G^{\mathrm {ab}}_{\mathbf {Q}_{p}}$
corresponding to
$\sigma \in G^{\mathrm {ab}}_{\mathbf {Q}_{p}}$
corresponding to
![]() $a\in \mathbf {Q}_{p}^{\times }$
under the reciprocity map, we have
$a\in \mathbf {Q}_{p}^{\times }$
under the reciprocity map, we have
For now until the final Section 4.5.3, we fix an embedding
by which we identify the fixed standard character
![]() $\psi ^{\infty }\colon \mathbf {A}^{\infty }\to \mathbf {C}$
with one valued in
$\psi ^{\infty }\colon \mathbf {A}^{\infty }\to \mathbf {C}$
with one valued in
![]() $\mathbf {Q}_{p}^{\mathrm {ab}}$
(still denoted by
$\mathbf {Q}_{p}^{\mathrm {ab}}$
(still denoted by
![]() $\psi ^{\infty }$
).
$\psi ^{\infty }$
).
4.1 Petersson product
Let
![]() $\pi $
be an ordinary automorphic representation of
$\pi $
be an ordinary automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
over a finite extension L of
$\mathrm {G}(\mathbf {A})$
over a finite extension L of
![]() $\mathbf {Q}_{p}^{\mathrm {ab}}$
. For
$\mathbf {Q}_{p}^{\mathrm {ab}}$
. For
![]() $v \vert p$
, let
$v \vert p$
, let
![]() $\omega _{\pi ,v}$
,
$\omega _{\pi ,v}$
,
![]() $ \alpha _{\pi ,v}\colon F_{v}^{\times }\to L^{\times }$
be the central character and, respectively,
$ \alpha _{\pi ,v}\colon F_{v}^{\times }\to L^{\times }$
be the central character and, respectively,
![]() $\mathrm {U}_{v}$
-eigencharacter of
$\mathrm {U}_{v}$
-eigencharacter of
![]() $\pi _{v}$
.
$\pi _{v}$
.
Define
![]() $\gamma ( \mathrm {ad} (V_{\pi ,p})(1)^{++}, \psi _{p}):=\prod _{v\vert p} \gamma ( \mathrm {ad} (V_{\pi ,v})(1)^{++}, \psi _{v})$
, where
$\gamma ( \mathrm {ad} (V_{\pi ,p})(1)^{++}, \psi _{p}):=\prod _{v\vert p} \gamma ( \mathrm {ad} (V_{\pi ,v})(1)^{++}, \psi _{v})$
, where
![]() $\mathrm {ad} (V_{\pi ,p})(1)^{++}$
is the character
$\mathrm {ad} (V_{\pi ,p})(1)^{++}$
is the character
![]() $\omega _{\pi , v}^{-1}\alpha _{\pi , v}^{2}|\cdot |^{2}$
of
$\omega _{\pi , v}^{-1}\alpha _{\pi , v}^{2}|\cdot |^{2}$
of
![]() $F_{v}^{\times }$
. For
$F_{v}^{\times }$
. For
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
, let
$\iota \colon L\hookrightarrow \mathbf {C}$
, let
 $$ \begin{align*}e_{p}(\mathrm{ad}(V_{\pi^{\iota}})(1)):= {\gamma(\iota \mathrm{ad} (V_{\pi,p})(1)^{++}, \psi_{p})^{-1} \zeta_{F, p}(2) \over L(1, \pi_{p}^{\iota}, \mathrm{ad}) }.\end{align*} $$
$$ \begin{align*}e_{p}(\mathrm{ad}(V_{\pi^{\iota}})(1)):= {\gamma(\iota \mathrm{ad} (V_{\pi,p})(1)^{++}, \psi_{p})^{-1} \zeta_{F, p}(2) \over L(1, \pi_{p}^{\iota}, \mathrm{ad}) }.\end{align*} $$
Let
![]() $(, )$
denote the Petersson pairing
$(, )$
denote the Petersson pairing
of automorphic forms on
![]() $\mathrm {G}(\mathbf {A})$
.
$\mathrm {G}(\mathbf {A})$
.
Lemma 4.1 Let
![]() $\pi $
be an ordinary cuspidal automorphic representation of
$\pi $
be an ordinary cuspidal automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
of weight
$\mathrm {G}(\mathbf {A})$
of weight
![]() $\underline {w}$
over a finite extension L of
$\underline {w}$
over a finite extension L of
![]() $\mathbf {Q}_{p}^{\mathrm {ab}}$
. There exists a bilinear pairing
$\mathbf {Q}_{p}^{\mathrm {ab}}$
. There exists a bilinear pairing
such that for all
![]() $\iota \colon L\hookrightarrow \mathbf {C}$
extending
$\iota \colon L\hookrightarrow \mathbf {C}$
extending
![]() $\iota ^{\mathrm {ab}}=(4.0.2)$
and all sufficiently large
$\iota ^{\mathrm {ab}}=(4.0.2)$
and all sufficiently large
![]() $r\in \mathbf {N}^{S_{p}}$
,
$r\in \mathbf {N}^{S_{p}}$
,
 $$ \begin{align}\begin{aligned} \iota \langle f ,g \rangle = { {|D_{F}|^{1/2} \zeta_{F}(2) \over \omega_{\pi^{\iota}, p}(-1) e_{p}(\mathrm{ad}(V_{\pi^{\iota}})(1)) \cdot 2^{\sum_{\sigma}-1- w_{\sigma}}\cdot L(1, \pi^{\iota}, \mathrm{ad})} {q_{F,p}^{r}(w_{r,p} \mathrm{U}_{p}^{-r} f^{\iota, \rm a}, {g}^{\iota})} }. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \iota \langle f ,g \rangle = { {|D_{F}|^{1/2} \zeta_{F}(2) \over \omega_{\pi^{\iota}, p}(-1) e_{p}(\mathrm{ad}(V_{\pi^{\iota}})(1)) \cdot 2^{\sum_{\sigma}-1- w_{\sigma}}\cdot L(1, \pi^{\iota}, \mathrm{ad})} {q_{F,p}^{r}(w_{r,p} \mathrm{U}_{p}^{-r} f^{\iota, \rm a}, {g}^{\iota})} }. \end{aligned}\end{align} $$
The pairing
![]() $\langle \, , \, \rangle $
satisfies the following properties.
$\langle \, , \, \rangle $
satisfies the following properties.
-
(1) For all
 $f\in \pi ^{\mathrm {ord}}$
and
$f\in \pi ^{\mathrm {ord}}$
and
 $g\in N_{\underline {w}^{\vee }}(L)$
, we have
$g\in N_{\underline {w}^{\vee }}(L)$
, we have
 $\langle f ,g \rangle =\langle f, e^{\mathrm {ord}} e^{\mathrm {hol}} g\rangle $
.
$\langle f ,g \rangle =\langle f, e^{\mathrm {ord}} e^{\mathrm {hol}} g\rangle $
. -
(2) If
 $f_{0}\in \pi ^{\infty }$
and
$f_{0}\in \pi ^{\infty }$
and
 $f_{0}^{\vee }\in \pi ^{\vee ,\infty }$
are ordinary forms, new at places away from p, holomorphic at the infinite places, and with first Fourier coefficients equal to
$f_{0}^{\vee }\in \pi ^{\vee ,\infty }$
are ordinary forms, new at places away from p, holomorphic at the infinite places, and with first Fourier coefficients equal to
 $1$
, then (4.1.2)for some constant
$1$
, then (4.1.2)for some constant $$ \begin{align}\begin{aligned} \langle f_{0}, f_{0}^{\vee} \rangle = c_{\pi^{\infty}} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \langle f_{0}, f_{0}^{\vee} \rangle = c_{\pi^{\infty}} \end{aligned}\end{align} $$
 $c_{\pi ^{\infty }}\in L^{\times }$
depending only on the Bernstein components and the monodromy of
$c_{\pi ^{\infty }}\in L^{\times }$
depending only on the Bernstein components and the monodromy of
 $\pi _{v}$
for all
$\pi _{v}$
for all
 $v\nmid p\infty $
.
$v\nmid p\infty $
.
Proof The existence and (4.1.2) follow from the factorization of the Petersson inner product into parings in the Whittaker models [Reference Cai and FanCST14, Proposition 2.1], together with the local calculations of [Reference Cai and FanCST14, Proposition 3.11] away from p and [Reference DisegniDis/b, Lemma A.3.3] at p. Since the elements
![]() $f^{\iota , \rm a}$
in the right-hand side of (4.1.1) are antiholomorphic, it is clear that the pairing factors through
$f^{\iota , \rm a}$
in the right-hand side of (4.1.1) are antiholomorphic, it is clear that the pairing factors through
![]() $e^{\mathrm {hol}}$
.
$e^{\mathrm {hol}}$
.
Proposition 4.2 Let
![]() $\mathscr {X}_{\mathrm {G}}\subset \mathscr {Y}_{\mathrm {G}}$
be a Hida family of tame level
$\mathscr {X}_{\mathrm {G}}\subset \mathscr {Y}_{\mathrm {G}}$
be a Hida family of tame level
![]() $U^{p}$
, let S be a finite set of places such that
$U^{p}$
, let S be a finite set of places such that
![]() $U^{Sp}$
is maximal, and let
$U^{Sp}$
is maximal, and let
![]() $\Pi = \Pi _{\mathscr {X}_{\mathrm {G}}}^{U^{Sp}}$
. There is a unique
$\Pi = \Pi _{\mathscr {X}_{\mathrm {G}}}^{U^{Sp}}$
. There is a unique
![]() $\mathscr {O}({\mathscr {Y}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}})$
-bilinear pairing
$\mathscr {O}({\mathscr {Y}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}})$
-bilinear pairing
such that for all
![]() $x\in \mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}$
, corresponding to an ordinary representation
$x\in \mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}$
, corresponding to an ordinary representation
![]() $\pi =\pi _{x}$
over
$\pi =\pi _{x}$
over
![]() $\mathbf {Q}_{p}^{\mathrm {ab}}(x)$
, and for all
$\mathbf {Q}_{p}^{\mathrm {ab}}(x)$
, and for all
![]() $\mathbf {f}\in \Pi _{\mathbf {Q}_{p}^{\mathrm {ab}}}$
,
$\mathbf {f}\in \Pi _{\mathbf {Q}_{p}^{\mathrm {ab}}}$
,
![]() $\mathbf {g}\in {\mathscr {S}}^{\curlyvee }(\mathscr {Y}_{\mathrm {G}})_{\mathbf {Q}_{p}^{\mathrm {ab}}}$
, we have
$\mathbf {g}\in {\mathscr {S}}^{\curlyvee }(\mathscr {Y}_{\mathrm {G}})_{\mathbf {Q}_{p}^{\mathrm {ab}}}$
, we have
Proof The construction is very similar to that of the pairing denoted by
![]() $H^{-1}l_{\lambda }$
in [Reference HidaHid91, p. 380]. In this case, let
$H^{-1}l_{\lambda }$
in [Reference HidaHid91, p. 380]. In this case, let
![]() $\mathbf {f}_{0}^{\curlyvee }=(2.4.10)$
be the normalized primitive form in
$\mathbf {f}_{0}^{\curlyvee }=(2.4.10)$
be the normalized primitive form in
![]() $\Pi ^{\curlyvee }$
, let
$\Pi ^{\curlyvee }$
, let
![]() $U_{0}^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
be a maximal open compact subgroup fixing
$U_{0}^{p}\subset \mathrm {G}(\mathbf {A}^{p\infty })$
be a maximal open compact subgroup fixing
![]() $\mathbf {f}_{0}^{\curlyvee }$
, and let
$\mathbf {f}_{0}^{\curlyvee }$
, and let
be the unique
![]() $\mathscr {H}_{U_{0}^{p}}^{\mathrm {sph}}$
-equivariant idempotent that factors through the idempotent projection
$\mathscr {H}_{U_{0}^{p}}^{\mathrm {sph}}$
-equivariant idempotent that factors through the idempotent projection
![]() $\mathscr {S}^{\curlyvee }\to \mathscr {S}^{U_{0}^{p},\curlyvee }$
. Then we define
$\mathscr {S}^{\curlyvee }\to \mathscr {S}^{U_{0}^{p},\curlyvee }$
. Then we define
![]() $\langle \langle \mathbf {f}_{0}, - \rangle \rangle $
by
$\langle \langle \mathbf {f}_{0}, - \rangle \rangle $
by
where
![]() $c_{\mathscr {X}_{\mathrm {G}}}:=c_{\pi ^{\infty }}$
for any automorphic representation
$c_{\mathscr {X}_{\mathrm {G}}}:=c_{\pi ^{\infty }}$
for any automorphic representation
![]() $\pi $
such that
$\pi $
such that
![]() $\pi ^{U^{Sp},\mathrm {ord}}\cong \Pi _{|x}$
, for some
$\pi ^{U^{Sp},\mathrm {ord}}\cong \Pi _{|x}$
, for some
![]() $x\in \mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}$
. Let us explain why this is well defined independently of x. As noted before,
$x\in \mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}$
. Let us explain why this is well defined independently of x. As noted before,
![]() $c_{\pi ^{\infty }}$
only depends on the Bernstein component and the (rank of the) monodromy of
$c_{\pi ^{\infty }}$
only depends on the Bernstein component and the (rank of the) monodromy of
![]() $\pi _{x, v}$
for
$\pi _{x, v}$
for
![]() $v\nmid p\infty $
. (In plain terms, the rank of the monodromy is
$v\nmid p\infty $
. (In plain terms, the rank of the monodromy is
![]() $1$
if
$1$
if
![]() $\pi _{x, v}$
is a special representation and it is
$\pi _{x, v}$
is a special representation and it is
![]() $0$
otherwise.) The Bernstein component is an invariant of connected families. As for the rank of the monodromy, by the local–global compatibility result of Proposition 2.4, it is the rank of the monodromy of the Weil–Deligne representation attached to
$0$
otherwise.) The Bernstein component is an invariant of connected families. As for the rank of the monodromy, by the local–global compatibility result of Proposition 2.4, it is the rank of the monodromy of the Weil–Deligne representation attached to
![]() $\mathscr {V}_{\mathrm {G} |x}$
. Since the latter is pure, the desired constancy along
$\mathscr {V}_{\mathrm {G} |x}$
. Since the latter is pure, the desired constancy along
![]() $\mathscr {X}_{\mathrm {G}}$
follows from [Reference DisegniDis20, Proposition 3.3.1].
$\mathscr {X}_{\mathrm {G}}$
follows from [Reference DisegniDis20, Proposition 3.3.1].
In general, we may write
![]() $\mathbf {f}= T\mathbf {f}_{0}$
for some Hecke operator T supported away from p. We then define
$\mathbf {f}= T\mathbf {f}_{0}$
for some Hecke operator T supported away from p. We then define
![]() $\langle \langle \mathbf {f}, \mathbf {g}\rangle \rangle := \langle \langle \mathbf {f}_{0}, T^{\curlyvee }\mathbf {g}\rangle \rangle $
. The interpolation property follows from the definitions, the interpolation property proved in [Reference HidaHid91, Lemma 9.3], and (4.1.2).
$\langle \langle \mathbf {f}, \mathbf {g}\rangle \rangle := \langle \langle \mathbf {f}_{0}, T^{\curlyvee }\mathbf {g}\rangle \rangle $
. The interpolation property follows from the definitions, the interpolation property proved in [Reference HidaHid91, Lemma 9.3], and (4.1.2).
4.2 Waldspurger’s Rankin–Selberg integral
We recall the local and global theory of Waldspurger’s [Reference WaldspurgerWal85] integral representation of our L-function.
4.2.1 Setup
Let
![]() $y\in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}(\mathbf {C})$
, let
$y\in \mathscr {Y}_{\mathrm {H}}^{\mathrm {cl}}(\mathbf {C})$
, let
![]() $\chi =\chi _{y}$
be the corresponding character of
$\chi =\chi _{y}$
be the corresponding character of
![]() $E^{\times }\backslash \mathbf {A}_{E}^{\times }$
, let
$E^{\times }\backslash \mathbf {A}_{E}^{\times }$
, let
![]() $\underline {\kappa }_{\chi } \in \frak W^{\mathrm {cl}}(\mathbf {C})$
be its weight, let
$\underline {\kappa }_{\chi } \in \frak W^{\mathrm {cl}}(\mathbf {C})$
be its weight, let
![]() $\underline {l}$
be its numerical weight, and let
$\underline {l}$
be its numerical weight, and let
![]() $\omega _{\chi }:= \chi _{|\mathbf {A}^{\times }}$
.
$\omega _{\chi }:= \chi _{|\mathbf {A}^{\times }}$
.
Let
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C})$
, corresponding to a point
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}(\mathbf {C})$
, corresponding to a point
![]() $x_{0}\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and an embedding
$x_{0}\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and an embedding
![]() $\iota \colon \mathbf {Q}_{p}(x)\hookrightarrow \mathbf {C}$
. Let
$\iota \colon \mathbf {Q}_{p}(x)\hookrightarrow \mathbf {C}$
. Let
![]() $\pi _{0}$
be the ordinary automorphic representation of
$\pi _{0}$
be the ordinary automorphic representation of
![]() $\mathrm {G}(\mathbf {A})$
over
$\mathrm {G}(\mathbf {A})$
over
![]() $\mathbf {Q}_{p}(x_{0})$
attached to
$\mathbf {Q}_{p}(x_{0})$
attached to
![]() $x_{0}$
, and let
$x_{0}$
, and let
![]() $\pi =\pi _{0}^{\iota }$
. We denote by
$\pi =\pi _{0}^{\iota }$
. We denote by
respectively, the weight, numerical weight, and central character of
![]() $\pi $
. We let
$\pi $
. We let
![]() $\alpha =\otimes _{v}\alpha _{v}\colon F_{p}^{\times }\to \mathbf {C}^{\times }$
be the character such that
$\alpha =\otimes _{v}\alpha _{v}\colon F_{p}^{\times }\to \mathbf {C}^{\times }$
be the character such that
![]() $\mathrm {U}_{y}f^{\iota }=\alpha (t) f^{\iota }$
for any
$\mathrm {U}_{y}f^{\iota }=\alpha (t) f^{\iota }$
for any
![]() $f\in \pi _{0}^{\mathrm {ord}}$
and
$f\in \pi _{0}^{\mathrm {ord}}$
and
![]() $t\in F_{p}^{\times }$
. Then
$t\in F_{p}^{\times }$
. Then
are the decompositions of
![]() $\kappa _{\pi , 0}$
and
$\kappa _{\pi , 0}$
and
![]() $\kappa _{\pi }$
into a product of a smooth and an algebraic character.
$\kappa _{\pi }$
into a product of a smooth and an algebraic character.
Define, as in Corollary 3.15, a numerical weight
![]() $\underline {k}$
and a smooth character
$\underline {k}$
and a smooth character
![]() $\kappa _{2}'$
of
$\kappa _{2}'$
of
![]() $U_{F, p}^{\circ }$
by
$U_{F, p}^{\circ }$
by
 $$ \begin{align}\begin{aligned} \kappa_{\chi}' \kappa_{2}' &= \kappa_{\pi^{\vee}}' = \alpha_{|U_{F, p}^{\circ}}, \qquad &\xi=\omega_{\pi}\omega_{\chi},\\ k &= (w-2- | l | -k_{0})/2, \qquad &k_{0}=w_{0}+l_{0}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \kappa_{\chi}' \kappa_{2}' &= \kappa_{\pi^{\vee}}' = \alpha_{|U_{F, p}^{\circ}}, \qquad &\xi=\omega_{\pi}\omega_{\chi},\\ k &= (w-2- | l | -k_{0})/2, \qquad &k_{0}=w_{0}+l_{0}, \end{aligned}\end{align} $$
and let
![]() $\underline {\kappa }_{2}\in \frak W(\mathbf {C})$
be the associated weight as in (3.4.6).
$\underline {\kappa }_{2}\in \frak W(\mathbf {C})$
be the associated weight as in (3.4.6).
For
![]() $v\vert p$
, we choose a Schwartz function
$v\vert p$
, we choose a Schwartz function
![]() $\Phi _{v}=\phi _{v}\in \mathcal {S}(\mathbf {V}_{v}\times F_{v}^{\times })$
as in (3.4.1) and (3.4.3) (for
$\Phi _{v}=\phi _{v}\in \mathcal {S}(\mathbf {V}_{v}\times F_{v}^{\times })$
as in (3.4.1) and (3.4.3) (for
![]() $\phi _{1}$
), and (3.3.11) and (4.2.1) (for
$\phi _{1}$
), and (3.3.11) and (4.2.1) (for
![]() $\phi _{2}$
); then
$\phi _{2}$
); then
For
![]() $v\vert \infty $
, let
$v\vert \infty $
, let
![]() $\Phi _{v}=\Phi _{l_{0}, l, k_{0}, k, v}$
be a preimage, under the map (3.1.1), of
$\Phi _{v}=\Phi _{l_{0}, l, k_{0}, k, v}$
be a preimage, under the map (3.1.1), of
4.2.2 Waldspurger’s integral
The next proposition gives an integral representation for the L-function we are interested in. We first define the local terms. Let
![]() $f_{0}\in \pi _{0}^{\mathrm {ord}}$
, let
$f_{0}\in \pi _{0}^{\mathrm {ord}}$
, let
![]() $f:= f_{0}^{\iota }$
, and let
$f:= f_{0}^{\iota }$
, and let
 $$ \begin{align*}\overline{W}(g):=\int_{F\backslash \mathbf{A}} f^{\mathrm{a}}\left( \left(\begin{array}{cc}1&x\\&1\end{array}\right) g\right)\psi(x)\, dx\end{align*} $$
$$ \begin{align*}\overline{W}(g):=\int_{F\backslash \mathbf{A}} f^{\mathrm{a}}\left( \left(\begin{array}{cc}1&x\\&1\end{array}\right) g\right)\psi(x)\, dx\end{align*} $$
be the Whittaker function of
![]() $f^{\mathrm {a}}$
with respect to
$f^{\mathrm {a}}$
with respect to
![]() $\psi ^{-1}$
. It is related to the q-expansion (2.2.1) of f by
$\psi ^{-1}$
. It is related to the q-expansion (2.2.1) of f by
 $$ \begin{align*}\overline{W}\left(\left(\begin{array}{cc}y&\\&1\end{array}\right)\right)= W_{f}^{\mathbf{C}} (y).\end{align*} $$
$$ \begin{align*}\overline{W}\left(\left(\begin{array}{cc}y&\\&1\end{array}\right)\right)= W_{f}^{\mathbf{C}} (y).\end{align*} $$
We assume that
![]() $W\colon \mathrm {G}(\mathbf {A})\to \mathbf {C}$
is factorizable as
$W\colon \mathrm {G}(\mathbf {A})\to \mathbf {C}$
is factorizable as
![]() $\overline {W}=\otimes _{v}\overline {W}_{v}$
.
$\overline {W}=\otimes _{v}\overline {W}_{v}$
.
For
![]() $\Phi =\otimes _{v}\Phi _{v}\in \mathcal {S}(\mathbf {V}\times \mathbf {A}^{\times })$
, let
$\Phi =\otimes _{v}\Phi _{v}\in \mathcal {S}(\mathbf {V}\times \mathbf {A}^{\times })$
, let
 $$ \begin{align*}&R_{r,v}( \overline W_{v}, \Phi_{v}, \chi_{v})\\ &\quad:= \int_{Z(F_{v})N(F_{v})\backslash \mathrm{G}(F_{v})}\overline W_{v}(g) \delta_{\xi_{v}, r}(g) \int_{T(F_{v})} \chi_{v}(t) r(gw_{r,v}^{-1})\Phi_{v}(t^{-1}, q(t))\, dt\, dg,\end{align*} $$
$$ \begin{align*}&R_{r,v}( \overline W_{v}, \Phi_{v}, \chi_{v})\\ &\quad:= \int_{Z(F_{v})N(F_{v})\backslash \mathrm{G}(F_{v})}\overline W_{v}(g) \delta_{\xi_{v}, r}(g) \int_{T(F_{v})} \chi_{v}(t) r(gw_{r,v}^{-1})\Phi_{v}(t^{-1}, q(t))\, dt\, dg,\end{align*} $$
where
![]() $\delta _{\xi , r}$
is as in (3.3.1). Note that the integral
$\delta _{\xi , r}$
is as in (3.3.1). Note that the integral
![]() $R_{r,v}$
does not depend on
$R_{r,v}$
does not depend on
![]() $r\geq \underline {1}$
unless
$r\geq \underline {1}$
unless
![]() $v\vert p$
; we will accordingly simplify the notation in these cases. We also define normalized versions. For
$v\vert p$
; we will accordingly simplify the notation in these cases. We also define normalized versions. For
![]() $v\vert p\infty $
, let
$v\vert p\infty $
, let
![]() $\Phi _{v}$
be as fixed in Section 4.2.1. Then we put
$\Phi _{v}$
be as fixed in Section 4.2.1. Then we put
 $$ \begin{align*}\begin{aligned} R_{v}^{\natural}(\overline W_{v},\Phi_{v}, \chi_{v}) &:= { |d_{v}|^{-2} |D_{v}|^{-1/2}} { \zeta_{F, v}(2)L(1, \eta_{v}\xi_{v})\over L(1/2, \pi_{E,v}\otimes \chi_{v})} R_{v}( \overline W_{v},\Phi_{v},\chi_{v}), & \ \text{if}\ v\nmid p\infty, \\ R_{r,v}^{\dagger}(\overline W_{v} ,\chi_{v}, \alpha_{v}) &: = { |d_{v}|^{-2} |D_{v}|^{-1/2}} { \zeta_{F, v}(2)L(1, \eta_{v})\over L(1/2, \pi_{E,v}\otimes \chi_{v})} q_{F, v}^{r}\alpha_{v}^{-r} R_{r,v}( \overline W_{v}, \Phi_{v}, \chi_{v}), &\ \text{if}\ v\vert p,\\ R_{v}^{\dagger}(\overline W_{v}, \chi_{v}, k) &: = { \zeta_{F, v}(2)L(1, \eta_{v})\over L(1/2, \pi_{E,v}\otimes \chi_{v})} R_{v}( \overline W_{v},\Phi_{v}, \chi_{v}), &\ \text{if}\ v\vert \infty. \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} R_{v}^{\natural}(\overline W_{v},\Phi_{v}, \chi_{v}) &:= { |d_{v}|^{-2} |D_{v}|^{-1/2}} { \zeta_{F, v}(2)L(1, \eta_{v}\xi_{v})\over L(1/2, \pi_{E,v}\otimes \chi_{v})} R_{v}( \overline W_{v},\Phi_{v},\chi_{v}), & \ \text{if}\ v\nmid p\infty, \\ R_{r,v}^{\dagger}(\overline W_{v} ,\chi_{v}, \alpha_{v}) &: = { |d_{v}|^{-2} |D_{v}|^{-1/2}} { \zeta_{F, v}(2)L(1, \eta_{v})\over L(1/2, \pi_{E,v}\otimes \chi_{v})} q_{F, v}^{r}\alpha_{v}^{-r} R_{r,v}( \overline W_{v}, \Phi_{v}, \chi_{v}), &\ \text{if}\ v\vert p,\\ R_{v}^{\dagger}(\overline W_{v}, \chi_{v}, k) &: = { \zeta_{F, v}(2)L(1, \eta_{v})\over L(1/2, \pi_{E,v}\otimes \chi_{v})} R_{v}( \overline W_{v},\Phi_{v}, \chi_{v}), &\ \text{if}\ v\vert \infty. \end{aligned}\end{align*} $$
By a result of Waldspurger (see [Reference DisegniDis17, Lemma 5.3.2]), for a place v such that
![]() $\pi _{v}$
and
$\pi _{v}$
and
![]() $\chi _{v}$
are unramified,
$\chi _{v}$
are unramified,
![]() $\phi _{v}$
is standard, and
$\phi _{v}$
is standard, and
![]() $\overline W_{v}$
is unramified, we have
$\overline W_{v}$
is unramified, we have
Proposition 4.3 Let
![]() $f_{0}\in \pi _{0}^{\mathrm {ord}}$
and assume that
$f_{0}\in \pi _{0}^{\mathrm {ord}}$
and assume that
![]() $f:=f_{0}^{\iota , \rm a}$
has a factorizable
$f:=f_{0}^{\iota , \rm a}$
has a factorizable
![]() $\psi ^{-1}$
-Whittaker function
$\psi ^{-1}$
-Whittaker function
![]() $\overline W=\otimes _{v} \overline W_{v}$
. Let
$\overline W=\otimes _{v} \overline W_{v}$
. Let
![]() $\phi ^{p\infty }\in \mathcal {S}(\mathbf {V}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
. For sufficiently large
$\phi ^{p\infty }\in \mathcal {S}(\mathbf {V}^{p\infty }\times \mathbf {A}^{p\infty , \times })$
. For sufficiently large
![]() $r=(r_{v})_{v\vert p}$
, we have
$r=(r_{v})_{v\vert p}$
, we have
 $$ \begin{align*} &\iota q_{F, p}^{r}\alpha(\varpi_{p})^{-r} ( f ,w_{r, p}^{-1} I(\phi^{p\infty}; \chi, \xi, \kappa_{2}', k)) = {|D_{F}|^{-1} |D_{E}|^{-1/2}} {L(1/2, \pi_{E}\otimes \chi)\over \zeta_{F}(2) L(1,\eta)}\\ &\qquad\qquad \cdot \prod_{v\nmid p\infty} R_{r,v}^{\natural}( \overline W_{v}, \phi_{v},\chi_{v}) \prod_{v\vert p } R_{r,v}^{\dagger}( \overline W_{v} ,\chi_{v}, \alpha_{v}) \prod_{v\vert \infty } R_{v}^{\dagger}(\overline W_{v} ,\chi_{v}, k), \end{align*} $$
$$ \begin{align*} &\iota q_{F, p}^{r}\alpha(\varpi_{p})^{-r} ( f ,w_{r, p}^{-1} I(\phi^{p\infty}; \chi, \xi, \kappa_{2}', k)) = {|D_{F}|^{-1} |D_{E}|^{-1/2}} {L(1/2, \pi_{E}\otimes \chi)\over \zeta_{F}(2) L(1,\eta)}\\ &\qquad\qquad \cdot \prod_{v\nmid p\infty} R_{r,v}^{\natural}( \overline W_{v}, \phi_{v},\chi_{v}) \prod_{v\vert p } R_{r,v}^{\dagger}( \overline W_{v} ,\chi_{v}, \alpha_{v}) \prod_{v\vert \infty } R_{v}^{\dagger}(\overline W_{v} ,\chi_{v}, k), \end{align*} $$
where all but finitely many of the factors in the infinite product are equal to
![]() $1$
.
$1$
.
Proof As in [Reference DisegniDis17, Proof of Proposition 3.5.1], corrected in [Reference DisegniDis/a, Appendix B, under “Proposition 2.4.4.1”] to include the factor
![]() $q_{F, p}^{r}$
.
$q_{F, p}^{r}$
.
4.2.3 Nonvanishing of the local integrals
We recall a fundamental nonvanishing result for our zeta integrals for self-dual
![]() $\pi \boxtimes \chi $
, as well as a useful refinement.
$\pi \boxtimes \chi $
, as well as a useful refinement.
Lemma 4.4 Let
![]() $v\nmid p\infty $
be a place of F, and let L be a field of characteristic zero. Let
$v\nmid p\infty $
be a place of F, and let L be a field of characteristic zero. Let
![]() $\pi _{v}$
be a smooth irreducible representation of
$\pi _{v}$
be a smooth irreducible representation of
![]() $\mathrm {G}(F_{v})$
over L, with central character
$\mathrm {G}(F_{v})$
over L, with central character
![]() $\omega _{\pi ,v}$
, and let
$\omega _{\pi ,v}$
, and let
![]() $\chi _{v}\colon E_{v}^{\times }\to L^{\times }$
be a smooth character. Assume the self-duality condition
$\chi _{v}\colon E_{v}^{\times }\to L^{\times }$
be a smooth character. Assume the self-duality condition
![]() $\omega _{\pi , v}\chi _{|F_{v}^{\times }}=\mathbf {1}$
.
$\omega _{\pi , v}\chi _{|F_{v}^{\times }}=\mathbf {1}$
.
There exist:
-
• a four-dimensional quadratic space
 $\mathbf {V}_{v} = \mathbf {B}_{v}$
over
$\mathbf {V}_{v} = \mathbf {B}_{v}$
over
 $F_{v}$
of the type described in Section 3.1.4, uniquely determined by
$F_{v}$
of the type described in Section 3.1.4, uniquely determined by  $$ \begin{align*}\varepsilon(\mathbf{B}_{v}) = \eta_{v}\chi_{v}(-1)\varepsilon(\pi_{E,v}\otimes\chi_{v}),\end{align*} $$
$$ \begin{align*}\varepsilon(\mathbf{B}_{v}) = \eta_{v}\chi_{v}(-1)\varepsilon(\pi_{E,v}\otimes\chi_{v}),\end{align*} $$
-
• a function
 $\overline W_{v}$
in the Whittaker model of
$\overline W_{v}$
in the Whittaker model of
 $\pi _{v}$
,
$\pi _{v}$
, -
• a Schwartz function
 $\phi _{v}\in \mathcal {S}(\mathbf {V}_{v}\times {F}_{v}^{\times }, L)$
,
$\phi _{v}\in \mathcal {S}(\mathbf {V}_{v}\times {F}_{v}^{\times }, L)$
,
such that
If moreover all the data are unramified at a place v inert in E, it is possible to choose
![]() $\overline W_{v}$
and
$\overline W_{v}$
and
![]() $\phi _{v}=\phi _{1, v}\phi _{2,v}$
such that
$\phi _{v}=\phi _{1, v}\phi _{2,v}$
such that
![]() $\phi _{2,v}(0, u)=0$
for all u (condition (
3.3.7
)).
$\phi _{2,v}(0, u)=0$
for all u (condition (
3.3.7
)).
Proof The argument in [Reference DisegniDis17, Proof of Proposition 3.7.1, second paragraph] applies verbatim to prove the first statement. Let us prove the second one. We drop all subscripts v. Fix an isomorphism
![]() $\mathbf {V}_{2}\cong E$
, and let us choose
$\mathbf {V}_{2}\cong E$
, and let us choose
![]() $\overline W$
to be a new vector,
$\overline W$
to be a new vector,
![]() $\phi _{1,v}$
to be the standard Schwartz function, and
$\phi _{1,v}$
to be the standard Schwartz function, and
Writing
![]() $\doteq $
for an equality up to nonzero scalars, by the Iwasawa decomposition
$\doteq $
for an equality up to nonzero scalars, by the Iwasawa decomposition
Let
![]() $U_{0}(\varpi ^{r})\subset U_{0}:=\mathrm {GL}_{2}(\mathscr {O}_{F})$
be the set of matrices which are upper-triangular modulo
$U_{0}(\varpi ^{r})\subset U_{0}:=\mathrm {GL}_{2}(\mathscr {O}_{F})$
be the set of matrices which are upper-triangular modulo
![]() $\varpi ^{r}$
. It is easy to verify that
$\varpi ^{r}$
. It is easy to verify that
![]() $\phi _{2}$
is invariant under
$\phi _{2}$
is invariant under
![]() $U_{0}(\varpi ^{r})$
for some r, and that
$U_{0}(\varpi ^{r})$
for some r, and that
![]() $U_{0}= U_{0}(\varpi ^{r})\sqcup \bigsqcup _{b\in \mathscr {O}_{F,v}/\varpi ^{t}} \left (\begin {smallmatrix}1&\\b&1\end {smallmatrix}\right ) U_{0}(\varpi )$
. Thus, the integral in
$U_{0}= U_{0}(\varpi ^{r})\sqcup \bigsqcup _{b\in \mathscr {O}_{F,v}/\varpi ^{t}} \left (\begin {smallmatrix}1&\\b&1\end {smallmatrix}\right ) U_{0}(\varpi )$
. Thus, the integral in
![]() $dg$
is a constant multiple of
$dg$
is a constant multiple of
 $$ \begin{align*}\begin{aligned} {\ }&{\quad } \int_{\mathscr{O}_{F}} r(w)[\psi(y^{-1}bq(tx')) \hat{\phi}(x', y^{-1}q(t))]_{|x=t^{-1}y} \, db \\ &= \int_{\mathscr{O}_{F}} \int_{E\times E} \psi( \mathrm{Tr}_{E/F} t x_{1} ) \psi(y^{-1}q(t) \cdot b q(x)) \mathbf{1}_{\mathscr{O}_{E}}(x_{1}) \widehat{\mathbf{1}_{\mathscr{O}_{E}^{\times}}}(x_{2}) \mathbf{1}_{\mathscr{O}_{F}}^{\times}(y^{-1}q(t))] \, dx db \\ &=\mathbf{1}_{\mathscr{O}_{F}}^{\times}(y^{-1}q(t)) \int_{\mathscr{O}_{F}} \widehat{\mathbf{1}_{\mathscr{O}_{E}}}(t) \int_{E}\psi(y^{-1}q(t) bq(x_{2}) \widehat{\mathbf{1}_{\mathscr{O}_{E}^{\times}}}(x_{2}) \, dx_{2}\, db \doteq \mathbf{1}_{\mathscr{O}_{E}}(t)\mathbf{1}_{\mathscr{O}_{F}}^{\times}(y^{-1}q(t)), \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} {\ }&{\quad } \int_{\mathscr{O}_{F}} r(w)[\psi(y^{-1}bq(tx')) \hat{\phi}(x', y^{-1}q(t))]_{|x=t^{-1}y} \, db \\ &= \int_{\mathscr{O}_{F}} \int_{E\times E} \psi( \mathrm{Tr}_{E/F} t x_{1} ) \psi(y^{-1}q(t) \cdot b q(x)) \mathbf{1}_{\mathscr{O}_{E}}(x_{1}) \widehat{\mathbf{1}_{\mathscr{O}_{E}^{\times}}}(x_{2}) \mathbf{1}_{\mathscr{O}_{F}}^{\times}(y^{-1}q(t))] \, dx db \\ &=\mathbf{1}_{\mathscr{O}_{F}}^{\times}(y^{-1}q(t)) \int_{\mathscr{O}_{F}} \widehat{\mathbf{1}_{\mathscr{O}_{E}}}(t) \int_{E}\psi(y^{-1}q(t) bq(x_{2}) \widehat{\mathbf{1}_{\mathscr{O}_{E}^{\times}}}(x_{2}) \, dx_{2}\, db \doteq \mathbf{1}_{\mathscr{O}_{E}}(t)\mathbf{1}_{\mathscr{O}_{F}}^{\times}(y^{-1}q(t)), \end{aligned}\end{align*} $$
where the last equality follows from interchanging the order of integration and observing that
![]() $\widehat {\mathbf {1}_{\mathscr {O}_{E}^{\times }}}(x_{2}) = \mathrm {vol}(\mathscr {O}_{E}^{\times })$
for
$\widehat {\mathbf {1}_{\mathscr {O}_{E}^{\times }}}(x_{2}) = \mathrm {vol}(\mathscr {O}_{E}^{\times })$
for
![]() $x_{2}\in \mathscr {O}_{E}$
.
$x_{2}\in \mathscr {O}_{E}$
.
The last quantity equals
![]() $\phi ^{\circ }(t^{-1}y, y^{-1}q(t))$
for the standard Schwartz function
$\phi ^{\circ }(t^{-1}y, y^{-1}q(t))$
for the standard Schwartz function
![]() $\phi ^{\circ }$
; therefore, the integral R is a constant multiple of the unramified integral, in particular, it is nonzero by (4.2.3).
$\phi ^{\circ }$
; therefore, the integral R is a constant multiple of the unramified integral, in particular, it is nonzero by (4.2.3).
4.3 Evaluation of the integrals at p and
 $\infty $
$\infty $
We explicitly compute the local integrals at the places
![]() $v \vert p\infty $
.
$v \vert p\infty $
.
4.3.1 p-adic integrals
Define, for
![]() $v\vert p$
,
$v\vert p$
,
 $$ \begin{align}\begin{aligned} e_{v}(V_{\pi_{E}\otimes \chi}) &:= { L(1/2, \pi_{E,v}\otimes\chi_{v}) \over \zeta_{F,v}(2) L(1, \eta_{v})} \prod_{w\vert v}\gamma(\chi_{w}\alpha_{\pi, v}|\cdot|\circ N_{E_{w}/F_{v}}, \psi_{v})^{-1},\\ e_{p}(V_{\pi_{E}\otimes \chi}) &:= \prod_{v\vert p} e_{v}(V_{\pi_{E}\otimes \chi}). \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} e_{v}(V_{\pi_{E}\otimes \chi}) &:= { L(1/2, \pi_{E,v}\otimes\chi_{v}) \over \zeta_{F,v}(2) L(1, \eta_{v})} \prod_{w\vert v}\gamma(\chi_{w}\alpha_{\pi, v}|\cdot|\circ N_{E_{w}/F_{v}}, \psi_{v})^{-1},\\ e_{p}(V_{\pi_{E}\otimes \chi}) &:= \prod_{v\vert p} e_{v}(V_{\pi_{E}\otimes \chi}). \end{aligned}\end{align} $$
Lemma 4.5 Let
![]() $v\vert p$
, and assume that
$v\vert p$
, and assume that
![]() $\overline W_{v}$
is normaliz,ed by
$\overline W_{v}$
is normaliz,ed by
![]() $\overline W_{v}(1)=1$
. Then for any sufficiently large r (depending on
$\overline W_{v}(1)=1$
. Then for any sufficiently large r (depending on
![]() $\chi _{v}$
,
$\chi _{v}$
,
![]() $\pi _{v}$
), we have
$\pi _{v}$
), we have
 $$ \begin{align*}R_{r,v}^{\dagger}(\overline W_{v},\chi_{v}, \alpha_{v}) ={\chi_{v}(-1) \over L(1, \eta_{v})} e_{v}(V_{\pi_{E}\otimes \chi}).\end{align*} $$
$$ \begin{align*}R_{r,v}^{\dagger}(\overline W_{v},\chi_{v}, \alpha_{v}) ={\chi_{v}(-1) \over L(1, \eta_{v})} e_{v}(V_{\pi_{E}\otimes \chi}).\end{align*} $$
Proof By [Reference DisegniDis17, Proposition A.2.2] (with the discriminant factors corrected as in [Reference DisegniDis/a, Appendix B]), we have
 $$ \begin{align*}R_{r,v}^{\dagger}(\overline W_{v},\phi_{v}, \chi_{v}) = {L(1/2, \pi_{E}\otimes\chi_{v}) \over \zeta_{F,v}(2) L(1, \eta_{v})^{2} } Z_{v}, \end{align*} $$
$$ \begin{align*}R_{r,v}^{\dagger}(\overline W_{v},\phi_{v}, \chi_{v}) = {L(1/2, \pi_{E}\otimes\chi_{v}) \over \zeta_{F,v}(2) L(1, \eta_{v})^{2} } Z_{v}, \end{align*} $$
where
![]() $Z_{v}$
are integrals defined in [Reference DisegniDis17, Lemma A.1.1]. By [Reference DisegniDis/a, Lemma A.1.1], we have
$Z_{v}$
are integrals defined in [Reference DisegniDis17, Lemma A.1.1]. By [Reference DisegniDis/a, Lemma A.1.1], we have
The asserted formula follows.
4.3.2 Archimedean integrals
We compute the local integrals
![]() $R_{v}^{\dagger }$
when
$R_{v}^{\dagger }$
when
![]() $v\vert \infty $
. The standard antiholomorphic Whittaker function for
$v\vert \infty $
. The standard antiholomorphic Whittaker function for
![]() $\psi ^{-1}$
of weight
$\psi ^{-1}$
of weight
![]() $(w_{0}, w)$
is
$(w_{0}, w)$
is
Lemma 4.6 Let
![]() $v\vert \infty $
, and let
$v\vert \infty $
, and let
![]() $\overline W_{v}$
be the standard antiholomorphic Whittaker function of weight
$\overline W_{v}$
be the standard antiholomorphic Whittaker function of weight
![]() $(w_{0}, w)$
for
$(w_{0}, w)$
for
![]() ${\psi }^{-1}$
. Then
${\psi }^{-1}$
. Then
Proof By the Iwasawa decomposition, we can uniquely write any
![]() $g\in \mathrm {GL}_{2}(\mathbf {R})$
as
$g\in \mathrm {GL}_{2}(\mathbf {R})$
as
 $$ \begin{align*}g=\left(\begin{array}{cc}1& \\x&\end{array}\right){1}\left(\begin{array}{cc}z&\\&z\end{array}\right) \left(\begin{array}{cc}y&\\&1\end{array}\right) \left(\begin{array}{cc}\cos \theta& \sin \theta\\-\sin\theta&{\cos\theta}\end{array}\right)\end{align*} $$
$$ \begin{align*}g=\left(\begin{array}{cc}1& \\x&\end{array}\right){1}\left(\begin{array}{cc}z&\\&z\end{array}\right) \left(\begin{array}{cc}y&\\&1\end{array}\right) \left(\begin{array}{cc}\cos \theta& \sin \theta\\-\sin\theta&{\cos\theta}\end{array}\right)\end{align*} $$
with
![]() $x\in \mathbf {R}$
,
$x\in \mathbf {R}$
,
![]() $z\in \mathbf {R}^{\times }$
,
$z\in \mathbf {R}^{\times }$
,
![]() $y\in \mathbf {R}^{\times }$
and
$y\in \mathbf {R}^{\times }$
and
![]() $\theta \in \mathbf {R}/2\pi \mathbf {Z}$
; the local Tamagawa measure is then
$\theta \in \mathbf {R}/2\pi \mathbf {Z}$
; the local Tamagawa measure is then
![]() $dg=dxd^{\times }z{d^{\times }y\over {|y|}}{d\theta \over 2}$
. Let
$dg=dxd^{\times }z{d^{\times }y\over {|y|}}{d\theta \over 2}$
. Let
![]() $\Phi _{v}=\Phi _{l_{0}, l, k_{0}, k, v}$
. We drop all subscripts v. Since the weights match, the integration over
$\Phi _{v}=\Phi _{l_{0}, l, k_{0}, k, v}$
. We drop all subscripts v. Since the weights match, the integration over
![]() $\mathrm {SO}(2, \mathbf {R})$
yields
$\mathrm {SO}(2, \mathbf {R})$
yields
![]() $1$
, and we have
$1$
, and we have
 $$ \begin{align*} &R= R(\overline W, \Phi, \chi) =\int_{\mathbf{R}^{\times}\times (\mathbf{R}^{\times} \backslash \mathbf{C}^{\times}) \times \mathbf{R}/2\pi\mathbf{Z}\times{\mathbf{R}^{\times}}} \\ &\quad\chi(tz)\omega_{\pi}(z) |y|^{(w+w_{0})/ 2} e^{-2\pi y} \xi^{-1}(z)|y| \Phi(yzt^{-1}, y^{-1}z^{-2}q(t))\, d^{\times}z {d\theta\over 2} {d^{\times}y\over |y|} \, dt. \end{align*} $$
$$ \begin{align*} &R= R(\overline W, \Phi, \chi) =\int_{\mathbf{R}^{\times}\times (\mathbf{R}^{\times} \backslash \mathbf{C}^{\times}) \times \mathbf{R}/2\pi\mathbf{Z}\times{\mathbf{R}^{\times}}} \\ &\quad\chi(tz)\omega_{\pi}(z) |y|^{(w+w_{0})/ 2} e^{-2\pi y} \xi^{-1}(z)|y| \Phi(yzt^{-1}, y^{-1}z^{-2}q(t))\, d^{\times}z {d\theta\over 2} {d^{\times}y\over |y|} \, dt. \end{align*} $$
By definition,
![]() $\omega _{\pi }\chi \xi ^{-1}(z)=1$
, so that the integration in
$\omega _{\pi }\chi \xi ^{-1}(z)=1$
, so that the integration in
![]() $d^{\times }z$
simply realizes the map
$d^{\times }z$
simply realizes the map
![]() $\Phi \mapsto \phi $
. Then
$\Phi \mapsto \phi $
. Then
 $$ \begin{align}\begin{aligned} R &= \pi \int_{\mathbf{R}^{\times}} \int_{\mathbf{R}^{\times} \backslash \mathbf{C}^{\times}} \chi(t) |y|^{(w+w_{0})/ 2} e^{-2\pi y} |y| \mathbf{1}_{\mathbf{R}^{+}}(y) P_{k}(0) y^{( |l |+l_{0})/ 2} \chi(t)^{-1} e^{-2\pi y} {d^{\times}y\over |y|} \, dt\\ &= 2\pi P_{k_{0},k}(0) \int_{\mathbf{R}^{+}} y^{(w+ | l | +w_{0}+l_{0}) / 2} e^{-4\pi y} {d^{\times}y}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} R &= \pi \int_{\mathbf{R}^{\times}} \int_{\mathbf{R}^{\times} \backslash \mathbf{C}^{\times}} \chi(t) |y|^{(w+w_{0})/ 2} e^{-2\pi y} |y| \mathbf{1}_{\mathbf{R}^{+}}(y) P_{k}(0) y^{( |l |+l_{0})/ 2} \chi(t)^{-1} e^{-2\pi y} {d^{\times}y\over |y|} \, dt\\ &= 2\pi P_{k_{0},k}(0) \int_{\mathbf{R}^{+}} y^{(w+ | l | +w_{0}+l_{0}) / 2} e^{-4\pi y} {d^{\times}y}, \end{aligned}\end{align} $$
where
![]() $2=\mathrm {vol}(\mathbf {R}^{\times }\backslash \mathbf {C}^{\times })$
.
$2=\mathrm {vol}(\mathbf {R}^{\times }\backslash \mathbf {C}^{\times })$
.
Recall from (4.2.1) and (3.3.2) that
![]() $k_{0}=w_{0}+l_{0}$
and
$k_{0}=w_{0}+l_{0}$
and
![]() $k=(w-2- | l | -k_{0})/2$
and that
$k=(w-2- | l | -k_{0})/2$
and that
![]() $P_{k_{0}, k}(0) = (2\pi i)^{-k_{0}} (4\pi )^{-k} (k+k_{0})!$
. Then, after a change of variables, we have
$P_{k_{0}, k}(0) = (2\pi i)^{-k_{0}} (4\pi )^{-k} (k+k_{0})!$
. Then, after a change of variables, we have
 $$ \begin{align*}\begin{aligned} R&= (2\pi)^{1-k_{0}} i^{-k_{0}} (4\pi)^{-(w- | l | - k_{0} -2 )/2} \Gamma({w-| l | +k_{0}\over 2}) (4\pi)^{-(w+| l |+k_{0}) / 2} \Gamma({w+| l |+k_{0}\over 2})\\ &= i^{-k_{0}} 2^{-1-w} \pi^{2} \Gamma_{\mathbf{C}}({w-l +k_{0}\over 2}) \Gamma_{\mathbf{C}}({w+l+k_{0}\over 2}). \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} R&= (2\pi)^{1-k_{0}} i^{-k_{0}} (4\pi)^{-(w- | l | - k_{0} -2 )/2} \Gamma({w-| l | +k_{0}\over 2}) (4\pi)^{-(w+| l |+k_{0}) / 2} \Gamma({w+| l |+k_{0}\over 2})\\ &= i^{-k_{0}} 2^{-1-w} \pi^{2} \Gamma_{\mathbf{C}}({w-l +k_{0}\over 2}) \Gamma_{\mathbf{C}}({w+l+k_{0}\over 2}). \end{aligned}\end{align*} $$
Now, the result follows from identifying
 $$ \begin{align*}\pi^{2} \Gamma_{\mathbf{C}}({w-l +k_{0}\over 2}) \Gamma_{\mathbf{C}}({w+l+k_{0}\over 2}) = {L(1, \pi_{E, v}\otimes\chi)\over \zeta_{F, v}(2) L(1, \eta_{v})}.\\[-42pt]\end{align*} $$
$$ \begin{align*}\pi^{2} \Gamma_{\mathbf{C}}({w-l +k_{0}\over 2}) \Gamma_{\mathbf{C}}({w+l+k_{0}\over 2}) = {L(1, \pi_{E, v}\otimes\chi)\over \zeta_{F, v}(2) L(1, \eta_{v})}.\\[-42pt]\end{align*} $$
4.4 Interpolation of the local zeta integral
Let
![]() $\mathscr {X}=\mathscr {X}_{\mathrm {G}} \hat {\times }\mathscr {X}_{\mathrm {H}}$
be a Hida family for
$\mathscr {X}=\mathscr {X}_{\mathrm {G}} \hat {\times }\mathscr {X}_{\mathrm {H}}$
be a Hida family for
![]() $\mathrm {G}\times \mathrm {H}$
, let
$\mathrm {G}\times \mathrm {H}$
, let
![]() $v\nmid p\infty $
be a place of F, and let
$v\nmid p\infty $
be a place of F, and let
![]() $\Pi _{v}:=\Pi (\mathscr {V}_{\mathrm {G},v})$
be as in Section 2.4.8. Let
$\Pi _{v}:=\Pi (\mathscr {V}_{\mathrm {G},v})$
be as in Section 2.4.8. Let
![]() $\mathscr {X}_{\mathrm {G}}^{(v)}\subset \mathscr {X}$
be the open subset containing
$\mathscr {X}_{\mathrm {G}}^{(v)}\subset \mathscr {X}$
be the open subset containing
![]() $\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
over which
$\mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
over which
![]() $\Pi _{v}$
is defined, and let
$\Pi _{v}$
is defined, and let
![]() $\mathscr {X}^{(v)}=\mathscr {X}_{\mathrm {G}}^{(v)}\hat {\times } \mathscr {X}_{\mathrm {H}}$
. Let
$\mathscr {X}^{(v)}=\mathscr {X}_{\mathrm {G}}^{(v)}\hat {\times } \mathscr {X}_{\mathrm {H}}$
. Let
![]() $\mathscr {W}_{v}$
be the
$\mathscr {W}_{v}$
be the
![]() $\psi _{v}$
-Whittaker model of
$\psi _{v}$
-Whittaker model of
![]() $\Pi _{v, \mathbf {Q}_{p}^{\mathrm {ab}}}$
, which exists since
$\Pi _{v, \mathbf {Q}_{p}^{\mathrm {ab}}}$
, which exists since
![]() $\Pi _{v}$
is co-Whittaker (see [Reference DisegniDis20, Section 4.2]); it is
$\Pi _{v}$
is co-Whittaker (see [Reference DisegniDis20, Section 4.2]); it is
![]() $\mathscr {O}_{\mathscr {X}^{(v)}}[\mathrm {G}(F_{v})]$
-isomorphic to the tensor product of
$\mathscr {O}_{\mathscr {X}^{(v)}}[\mathrm {G}(F_{v})]$
-isomorphic to the tensor product of
![]() $\Pi _{v}$
and an invertible sheaf with trivial
$\Pi _{v}$
and an invertible sheaf with trivial
![]() $\mathrm {G}(F_{v})$
-action. The space
$\mathrm {G}(F_{v})$
-action. The space
![]() $\mathscr {W}_{v}$
is, as usual, a space of functions on
$\mathscr {W}_{v}$
is, as usual, a space of functions on
![]() $\mathrm {G}(F_{v})$
,
$\mathrm {G}(F_{v})$
,
![]() $\psi _{v}$
-invariant under the action of the unipotent subgroup
$\psi _{v}$
-invariant under the action of the unipotent subgroup
![]() $N(F_{v})$
. For any
$N(F_{v})$
. For any
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and any
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
and any
![]() $\mathbf {W}_{v}\in \mathscr {W}_{v}$
, the twisted specialization
$\mathbf {W}_{v}\in \mathscr {W}_{v}$
, the twisted specialization
 $$ \begin{align*}\overline{\mathbf{W}}_{v|x}(g):= \mathbf{W}_{v|x}\left(\left(\begin{array}{cc}-1&\\&1\end{array}\right) g \left(\begin{array}{cc}-1&\\&1\end{array}\right)\right)\end{align*} $$
$$ \begin{align*}\overline{\mathbf{W}}_{v|x}(g):= \mathbf{W}_{v|x}\left(\left(\begin{array}{cc}-1&\\&1\end{array}\right) g \left(\begin{array}{cc}-1&\\&1\end{array}\right)\right)\end{align*} $$
belongs to the
![]() $\psi ^{-1}$
-Whittaker model of
$\psi ^{-1}$
-Whittaker model of
![]() $\pi _{x}$
.
$\pi _{x}$
.
Proposition 4.7 Let
![]() $v\nmid p\infty $
. There exists an
$v\nmid p\infty $
. There exists an
![]() $\mathscr {O}(\mathscr {X}^{(v)}_{\mathbf {Q}_{p}^{\mathrm {ab}}})$
-linear map
$\mathscr {O}(\mathscr {X}^{(v)}_{\mathbf {Q}_{p}^{\mathrm {ab}}})$
-linear map
such that for all
![]() $\mathbf {W}_{v}\in \mathscr {W}_{v}$
, all
$\mathbf {W}_{v}\in \mathscr {W}_{v}$
, all
![]() $\phi _{v}\in \mathcal {S}(\mathbf {V}_{v}\times F_{v}^{\times })$
, and all
$\phi _{v}\in \mathcal {S}(\mathbf {V}_{v}\times F_{v}^{\times })$
, and all
![]() $(x, y)\in \mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}(\mathbf {C})$
, with underlying embedding
$(x, y)\in \mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}(\mathbf {C})$
, with underlying embedding
![]() $\iota \colon \mathbf {Q}_{p}^{\mathrm {ab}}(x, y)\hookrightarrow \mathbf {C}$
, we have
$\iota \colon \mathbf {Q}_{p}^{\mathrm {ab}}(x, y)\hookrightarrow \mathbf {C}$
, we have
Proof In fact, we may prove a stronger statement by replacing
![]() $\mathscr {X}_{\mathrm {H}}$
by (its image in)
$\mathscr {X}_{\mathrm {H}}$
by (its image in)
![]() $\mathscr {Y}_{\mathrm {H}, v}$
, or equivalently any connected component
$\mathscr {Y}_{\mathrm {H}, v}$
, or equivalently any connected component
![]() $\mathscr {Y}_{\mathrm {H}, v}^{\circ }$
thereof (which is an étale torsor for
$\mathscr {Y}_{\mathrm {H}, v}^{\circ }$
thereof (which is an étale torsor for
![]() $\mathbf {G}_{m, \mathbf {Q}_{p}}^{\{w\vert v\}}$
, the action being induced by multiplication by the uniformizers in
$\mathbf {G}_{m, \mathbf {Q}_{p}}^{\{w\vert v\}}$
, the action being induced by multiplication by the uniformizers in
![]() $E_{v}^{\times }=\prod _{w\vert v}E_{w}^{\times }$
).
$E_{v}^{\times }=\prod _{w\vert v}E_{w}^{\times }$
).
The proof is largely similar to that of [Reference DisegniDis20, Proposition 5.2.3] (whose statement is corrected in Appendix B); we refer to loc. cit. and the sections preceding it for more details on the notions we use. Since
![]() $\mathscr {W}_{v}\cong \Pi (\mathscr {V}_{{\mathrm {G}},v})$
is in the image of the local Langlands correspondence, there exists an irreducible component
$\mathscr {W}_{v}\cong \Pi (\mathscr {V}_{{\mathrm {G}},v})$
is in the image of the local Langlands correspondence, there exists an irreducible component
![]() $\frak X^{\circ }$
of the extended Bernstein variety of [Reference DisegniDis20, Section 3.3] and a map
$\frak X^{\circ }$
of the extended Bernstein variety of [Reference DisegniDis20, Section 3.3] and a map
![]() $\mathscr {X}^{(v)}_{\mathrm {G}}\to \frak X^{\circ }$
, such that
$\mathscr {X}^{(v)}_{\mathrm {G}}\to \frak X^{\circ }$
, such that
![]() $\mathscr {W}_{v}$
is a quotient of the universal co-Whittaker module over
$\mathscr {W}_{v}$
is a quotient of the universal co-Whittaker module over
![]() $\frak X^{\circ }$
. We may further extend scalars to
$\frak X^{\circ }$
. We may further extend scalars to
![]() $\mathbf {C}$
and replace
$\mathbf {C}$
and replace
![]() $\frak X^{\circ }$
by a cover of the form
$\frak X^{\circ }$
by a cover of the form
for
![]() $d=1$
or
$d=1$
or
![]() $2$
; then the pull-back
$2$
; then the pull-back
![]() $\widetilde {\mathscr {W}}_{v}$
of the universal co-Whittaker module has one of the following shapes:
$\widetilde {\mathscr {W}}_{v}$
of the universal co-Whittaker module has one of the following shapes:
-
(a)
 $\widetilde {\mathscr {W}}_{v}=\mathrm {Ind}_{P_{v}}^{\mathrm {G}(F_{v})}(\beta _{1}\boxtimes \beta _{2})$
, where
$\widetilde {\mathscr {W}}_{v}=\mathrm {Ind}_{P_{v}}^{\mathrm {G}(F_{v})}(\beta _{1}\boxtimes \beta _{2})$
, where
 $d=2$
and
$d=2$
and
 $\beta _{i}\colon F_{v}^{\times }\to \mathscr {O}(\widetilde {\frak X}^{\circ })^{\times }$
are the universal characters;
$\beta _{i}\colon F_{v}^{\times }\to \mathscr {O}(\widetilde {\frak X}^{\circ })^{\times }$
are the universal characters; -
(b)
 $\widetilde {\mathscr {W}}_{v}=\mathrm {St}\otimes \beta _{1}$
, where
$\widetilde {\mathscr {W}}_{v}=\mathrm {St}\otimes \beta _{1}$
, where
 $d=1$
and
$d=1$
and
 $\beta _{1}\colon F_{v}^{\times } \to \mathscr {O}(\widetilde {\frak X}^{\circ })^{\times }$
is the universal character;
$\beta _{1}\colon F_{v}^{\times } \to \mathscr {O}(\widetilde {\frak X}^{\circ })^{\times }$
is the universal character; -
(c)
 $\widetilde {\mathscr {W}}_{v}=\pi _{0}\otimes \beta _{1}$
, where
$\widetilde {\mathscr {W}}_{v}=\pi _{0}\otimes \beta _{1}$
, where
 $\pi _{0}$
is a complex supercuspidal representation of
$\pi _{0}$
is a complex supercuspidal representation of
 $\mathrm {G}(F_{v})$
,
$\mathrm {G}(F_{v})$
,
 $d=1$
, and
$d=1$
, and
 $\beta _{1} \colon F_{v}^{\times } \to \mathscr {O}(\widetilde {\frak X}^{\circ })^{\times }$
is the universal character.
$\beta _{1} \colon F_{v}^{\times } \to \mathscr {O}(\widetilde {\frak X}^{\circ })^{\times }$
is the universal character.
In all cases, we need to show that for every
![]() $\mathbf {W}_{v}\in \widetilde {\mathscr {W}}_{v}$
, there is an element
$\mathbf {W}_{v}\in \widetilde {\mathscr {W}}_{v}$
, there is an element
![]() $\mathbf {R}_{v}(\mathbf {W}_{v}, \phi _{v}) \in \mathscr {O}( \widetilde {\frak X}^{\circ } \times \mathscr {Y}_{\mathrm {H}, v})$
such that
$\mathbf {R}_{v}(\mathbf {W}_{v}, \phi _{v}) \in \mathscr {O}( \widetilde {\frak X}^{\circ } \times \mathscr {Y}_{\mathrm {H}, v})$
such that
for all
![]() $x,y$
; in other words, that the power series in
$x,y$
; in other words, that the power series in
![]() $X_{i}^{\pm 1}:=\beta _{i}(\varpi _{v})^{\pm 1}$
and
$X_{i}^{\pm 1}:=\beta _{i}(\varpi _{v})^{\pm 1}$
and
![]() $Y_{w}^{\pm 1}:=\chi _{\mathrm {univ}}(\varpi _{w})^{\pm 1}$
obtained from the integral defining
$Y_{w}^{\pm 1}:=\chi _{\mathrm {univ}}(\varpi _{w})^{\pm 1}$
obtained from the integral defining
![]() $R_{v}$
is a Laurent-polynomial multiple of the inverse of the Laurent polynomial
$R_{v}$
is a Laurent-polynomial multiple of the inverse of the Laurent polynomial
![]() $L(1/2, \pi _{x, E, v}\otimes \chi _{y, v})$
. This is proved by the same argument as in [Reference DisegniDis17, Proof of Proposition 3.6.1]: since
$L(1/2, \pi _{x, E, v}\otimes \chi _{y, v})$
. This is proved by the same argument as in [Reference DisegniDis17, Proof of Proposition 3.6.1]: since
![]() $\widetilde {\mathscr {W}}_{v}$
is torsion-free, it embeds in the representation
$\widetilde {\mathscr {W}}_{v}$
is torsion-free, it embeds in the representation
![]() $\widetilde {\mathscr {W}}_{v}\otimes \mathscr {K}( \widetilde {\frak X}^{\circ })$
over the field
$\widetilde {\mathscr {W}}_{v}\otimes \mathscr {K}( \widetilde {\frak X}^{\circ })$
over the field
![]() $\mathscr {K}( \widetilde {\frak X}^{\circ })$
, so that the usual explicit description of the Kirillov model used in loc. cit. applies.
$\mathscr {K}( \widetilde {\frak X}^{\circ })$
, so that the usual explicit description of the Kirillov model used in loc. cit. applies.
4.5 The p-adic L-function
Let
be a Hida family with
![]() $\mathscr {X}^{\mathrm {sd}}\neq \emptyset $
, of tame level
$\mathscr {X}^{\mathrm {sd}}\neq \emptyset $
, of tame level
![]() $U^{p}=U_{\mathrm {G}}^{p}\times U_{\mathrm {H}}^{p}$
. Let S be a finite set of places of F, disjoint from
$U^{p}=U_{\mathrm {G}}^{p}\times U_{\mathrm {H}}^{p}$
. Let S be a finite set of places of F, disjoint from
![]() $S_{p\infty }$
and containing all those at which the tame level of
$S_{p\infty }$
and containing all those at which the tame level of
![]() $\mathscr {X}$
is not maximal, and let
$\mathscr {X}$
is not maximal, and let
![]() $\Pi :=\Pi ^{U_{\mathrm {G}}^{Sp}}_{\mathscr {X}_{\mathrm {G}}}$
. If
$\Pi :=\Pi ^{U_{\mathrm {G}}^{Sp}}_{\mathscr {X}_{\mathrm {G}}}$
. If
![]() $\mathscr {X}'$
is an (ind-)scheme over
$\mathscr {X}'$
is an (ind-)scheme over
![]() $\mathbf {Q}_{p}^{\mathrm {ab}}$
, we define
$\mathbf {Q}_{p}^{\mathrm {ab}}$
, we define
to be the subset of geometric points over
![]() $\iota ^{\mathrm {ab}}$
(that is, those such that the composition
$\iota ^{\mathrm {ab}}$
(that is, those such that the composition
![]() $\mathrm {Spec}\, \mathbf {C}\to \mathscr {X}^{\prime }_{\mathbf {Q}_{p}^{\mathrm {ab}}}\to \mathrm {Spec}\, \mathbf {Q}_{p}^{\mathrm {ab}}$
is
$\mathrm {Spec}\, \mathbf {C}\to \mathscr {X}^{\prime }_{\mathbf {Q}_{p}^{\mathrm {ab}}}\to \mathrm {Spec}\, \mathbf {Q}_{p}^{\mathrm {ab}}$
is
![]() $\iota ^{\mathrm {ab}, \sharp }$
).
$\iota ^{\mathrm {ab}, \sharp }$
).
4.5.1 Whittaker models and q-expansions in families
For
![]() $v\in S$
, let
$v\in S$
, let
![]() $\mathscr {X}_{(\mathrm {G})}^{(v)}\subset \mathscr {X}_{(\mathrm {G})}$
and
$\mathscr {X}_{(\mathrm {G})}^{(v)}\subset \mathscr {X}_{(\mathrm {G})}$
and
![]() $\mathscr {W}_{v}$
be as in Section 4.4, and let
$\mathscr {W}_{v}$
be as in Section 4.4, and let
![]() $\mathscr {X}_{(\mathrm {G})}':=\bigcap _{v\in S} \mathscr {X}_{(\mathrm {G})}^{(v)}$
; it contains
$\mathscr {X}_{(\mathrm {G})}':=\bigcap _{v\in S} \mathscr {X}_{(\mathrm {G})}^{(v)}$
; it contains
![]() $\mathscr {X}_{(\mathrm {G})}^{\mathrm {cl}}$
.
$\mathscr {X}_{(\mathrm {G})}^{\mathrm {cl}}$
.
Lemma 4.8 There is an isomorphism of
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}'}[\mathrm {G}(F_{S})]$
-modules
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}'}[\mathrm {G}(F_{S})]$
-modules
 $$ \begin{align}\begin{aligned} \mathbf{W}_{-, S}\colon \Pi_{\mathbf{Q}_{p}^{\mathrm{ab}}} &\stackrel{\cong}{\longrightarrow}\bigotimes_{v\in S} \mathscr{W}_{v},\\ \mathbf{f}&\mapsto \mathbf{W}_{\mathbf{f}, S}=\otimes_{v}\mathbf{W}_{\mathbf{f},v} \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbf{W}_{-, S}\colon \Pi_{\mathbf{Q}_{p}^{\mathrm{ab}}} &\stackrel{\cong}{\longrightarrow}\bigotimes_{v\in S} \mathscr{W}_{v},\\ \mathbf{f}&\mapsto \mathbf{W}_{\mathbf{f}, S}=\otimes_{v}\mathbf{W}_{\mathbf{f},v} \end{aligned}\end{align} $$
such that for all classical points
![]() $x\in \mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}$
and all
$x\in \mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}}$
and all
![]() $a_{S}\in F_{S}^{\times }$
, we have
$a_{S}\in F_{S}^{\times }$
, we have
 $$ \begin{align}\begin{aligned} \mathbf{W}_{\mathbf{f}, S}\left(\left(\begin{array}{cc}a_{S}&\\&1\end{array}\right)\right)(x) = W_{\mathbf{f}(x)^{}}(a_{S}1^{S\infty}),\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathbf{W}_{\mathbf{f}, S}\left(\left(\begin{array}{cc}a_{S}&\\&1\end{array}\right)\right)(x) = W_{\mathbf{f}(x)^{}}(a_{S}1^{S\infty}),\end{aligned}\end{align} $$
where the right-hand side is the p-adic q-expansion of
![]() $\mathbf {f} (x)$
defined in Section 2.3.2.
$\mathbf {f} (x)$
defined in Section 2.3.2.
Proof By Proposition 2.4 and [Reference DisegniDis20, Theorem 4.4.3], after possibly shrinking
![]() $\mathscr {X}_{\mathrm {G}}'$
, there exist an invertible sheaf
$\mathscr {X}_{\mathrm {G}}'$
, there exist an invertible sheaf
![]() $\mathscr {W}^{S, U^{S}}$
over
$\mathscr {W}^{S, U^{S}}$
over
![]() $\mathscr {X}^{\prime }_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}$
with trivial
$\mathscr {X}^{\prime }_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}$
with trivial
![]() $\mathrm {G}(F_{S})$
-action and an
$\mathrm {G}(F_{S})$
-action and an
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}'}[\mathrm {G}(F_{S})]$
-isomorphism
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}'}[\mathrm {G}(F_{S})]$
-isomorphism
unique up to
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}'}^{\times }$
, that we may write locally as
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}, \mathbf {Q}_{p}^{\mathrm {ab}}}'}^{\times }$
, that we may write locally as
where
![]() $\mathbf {W}^{S}(1^{S})$
is a section trivializing
$\mathbf {W}^{S}(1^{S})$
is a section trivializing
![]() $\mathscr {W}^{S, U^{S}}$
.
$\mathscr {W}^{S, U^{S}}$
.
For
![]() $v\notin S\cup S_{p\infty }$
and
$v\notin S\cup S_{p\infty }$
and
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, let
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
, let
![]() $\lambda _{x,v}\colon F_{v}^{\times }\to \mathbf {Q}_{p}(x)$
be the smooth function such that
$\lambda _{x,v}\colon F_{v}^{\times }\to \mathbf {Q}_{p}(x)$
be the smooth function such that
![]() $W_{v}(a)=\lambda _{x,v}(a) W_{v}(1)$
for any spherical element
$W_{v}(a)=\lambda _{x,v}(a) W_{v}(1)$
for any spherical element
![]() $W_{v}$
in the Kirillov model of
$W_{v}$
in the Kirillov model of
![]() $\pi _{x,v}$
; by the standard formulas (see, for instance, [Reference WaldspurgerWal85, p. 190]), there are functions
$\pi _{x,v}$
; by the standard formulas (see, for instance, [Reference WaldspurgerWal85, p. 190]), there are functions
![]() $\lambda _{v}\colon F_{v}^{\times }\to \mathscr {O}(\mathscr {X}_{\mathrm {G}})$
such that
$\lambda _{v}\colon F_{v}^{\times }\to \mathscr {O}(\mathscr {X}_{\mathrm {G}})$
such that
![]() $\lambda _{v}(x)=\lambda _{x,v}$
for all
$\lambda _{v}(x)=\lambda _{x,v}$
for all
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
. Let
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
. Let
![]() $\lambda ^{Sp}:=\otimes _{v\notin S\cup S_{p\infty }}\lambda _{v}$
, and let
$\lambda ^{Sp}:=\otimes _{v\notin S\cup S_{p\infty }}\lambda _{v}$
, and let
![]() $\alpha ^{\circ }_{p}\colon F_{p}^{\times }\to \mathscr {O}(\mathscr {X}_{\mathrm {G}})^{\times }$
be the
$\alpha ^{\circ }_{p}\colon F_{p}^{\times }\to \mathscr {O}(\mathscr {X}_{\mathrm {G}})^{\times }$
be the
![]() $\mathrm {U}_{p}^{\circ }$
-eigencharacter. Then we may define a pair of injective maps in
$\mathrm {U}_{p}^{\circ }$
-eigencharacter. Then we may define a pair of injective maps in
![]() $\mathrm {Hom}\,_{\mathscr {H}_{\mathrm {G}}^{\mathrm {ord}}} (\Pi , \mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}^{\mathbf {A}^{\infty , \times }})$
by
$\mathrm {Hom}\,_{\mathscr {H}_{\mathrm {G}}^{\mathrm {ord}}} (\Pi , \mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}^{\mathbf {A}^{\infty , \times }})$
by
where the former arises from (2.4.5) and interpolates the q-expansions
![]() $(W_{\mathbf {f}_{x}}(a))$
for
$(W_{\mathbf {f}_{x}}(a))$
for
![]() $x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
. By [Reference DisegniDis20, Lemma 4.2.5], the maps differ by a scalar in
$x\in \mathscr {X}_{\mathrm {G}}^{\mathrm {cl}}$
. By [Reference DisegniDis20, Lemma 4.2.5], the maps differ by a scalar in
![]() $\mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}$
. It follows that the invertible sheaf
$\mathscr {O}_{\mathscr {X}_{\mathrm {G}}'}$
. It follows that the invertible sheaf
![]() $\mathscr {W}^{S,U^{S}}$
is trivial, and that, from (4.5.3), we may deduce an isomorphism (4.5.1) normalized so as to satisfy (4.5.2)
$\mathscr {W}^{S,U^{S}}$
is trivial, and that, from (4.5.3), we may deduce an isomorphism (4.5.1) normalized so as to satisfy (4.5.2)
4.5.2 Definition of the p-adic L-function and interpolation property
For each classical point
![]() $(x,y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
and each place
$(x,y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
and each place
![]() $v\nmid p\infty $
, let
$v\nmid p\infty $
, let
![]() $\mathbf {V}_{(x, y),v}$
be the quadratic space given by the application of Lemma 4.4 to
$\mathbf {V}_{(x, y),v}$
be the quadratic space given by the application of Lemma 4.4 to
![]() $\pi _{x} $
and
$\pi _{x} $
and
![]() $\chi _{y}$
.
$\chi _{y}$
.
Lemma 4.9 The quadratic space
![]() $\mathbf {V}_{v}= \mathbf {V}_{(x, y),v}$
is independent of
$\mathbf {V}_{v}= \mathbf {V}_{(x, y),v}$
is independent of
![]() $(x,y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
.
$(x,y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
.
Proof This follows from the characterization in (3.1.3) and the constancy results for epsilon factors of [Reference DisegniDis20, Corollary 5.3.3].
Let
![]() $\mathbf {V}^{ p\infty }:= \otimes _{v\nmid p\infty }\mathbf {V}_{v}$
, and assume that S is not disjoint from the set
$\mathbf {V}^{ p\infty }:= \otimes _{v\nmid p\infty }\mathbf {V}_{v}$
, and assume that S is not disjoint from the set
![]() $S'$
of inert places v where
$S'$
of inert places v where
![]() $U^{p}$
is maximal. Let
$U^{p}$
is maximal. Let
be the set of those pairs
![]() $(\mathbf {f}, \phi ^{p\infty })$
such that
$(\mathbf {f}, \phi ^{p\infty })$
such that
![]() $\phi ^{Sp\infty }$
is standard, (3.3.7) holds at an inert place
$\phi ^{Sp\infty }$
is standard, (3.3.7) holds at an inert place
![]() $v\in S\cap S'$
, and the meromorphic function
$v\in S\cap S'$
, and the meromorphic function
![]() $\mathbf {R}_{v}(\mathbf {W}_{\mathbf {f}, v}, \phi _{v})$
on
$\mathbf {R}_{v}(\mathbf {W}_{\mathbf {f}, v}, \phi _{v})$
on
![]() $\mathscr {X}$
is nonzero for all
$\mathscr {X}$
is nonzero for all
![]() $v\in S$
.
$v\in S$
.
For
![]() $(\mathbf {f}, \phi ^{p\infty })\in \mathcal {A}$
, we define a meromorphic function
$(\mathbf {f}, \phi ^{p\infty })\in \mathcal {A}$
, we define a meromorphic function
 $$ \begin{align}\begin{aligned} \mathscr{L}_{p}(\mathscr{V}, \mathbf{f}, \phi^{p\infty})& \in \mathscr{K}(\mathscr{X}_{\mathbf{Q}_{p}^{\mathrm{ab}}}), \\ \mathscr{L}_{p}(\mathscr{V},\mathbf{f}, \phi^{p\infty})( x, y) & := C {\langle\langle \mathbf{f}_{x}, \mathbf{I}^{\mathrm{ord}, \curlyvee}(\phi^{p\infty}; x, y) \rangle \rangle \over \prod_{v\in S} \mathbf{R}_{v}(\mathbf{W}_{\mathbf{f}|x, v}, \phi_{v}, \chi_{y,v})}, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{L}_{p}(\mathscr{V}, \mathbf{f}, \phi^{p\infty})& \in \mathscr{K}(\mathscr{X}_{\mathbf{Q}_{p}^{\mathrm{ab}}}), \\ \mathscr{L}_{p}(\mathscr{V},\mathbf{f}, \phi^{p\infty})( x, y) & := C {\langle\langle \mathbf{f}_{x}, \mathbf{I}^{\mathrm{ord}, \curlyvee}(\phi^{p\infty}; x, y) \rangle \rangle \over \prod_{v\in S} \mathbf{R}_{v}(\mathbf{W}_{\mathbf{f}|x, v}, \phi_{v}, \chi_{y,v})}, \end{aligned}\end{align} $$
where we still denote by
![]() $\mathbf {I}^{\mathrm {ord}, \curlyvee }(\phi ^{p\infty })$
the restriction to
$\mathbf {I}^{\mathrm {ord}, \curlyvee }(\phi ^{p\infty })$
the restriction to
![]() $\mathscr {X}$
of the
$\mathscr {X}$
of the
![]() $(\mathscr {Y}_{\mathrm {G}}\hat {\times } \mathscr {Y}_{\mathrm {H}})$
-adic form of (3.4.10), and
$(\mathscr {Y}_{\mathrm {G}}\hat {\times } \mathscr {Y}_{\mathrm {H}})$
-adic form of (3.4.10), and
is a constant in
![]() $\mathbf {Q}^{\times }$
; here,
$\mathbf {Q}^{\times }$
; here,
![]() $\omega _{x}=\omega _{\pi _{x}}$
and
$\omega _{x}=\omega _{\pi _{x}}$
and
![]() $\omega _{y}=\omega _{\chi _{y}}$
. Note that the (base change of the) functional
$\omega _{y}=\omega _{\chi _{y}}$
. Note that the (base change of the) functional
![]() $\langle \langle {\mathbf {f}}, -\rangle \rangle $
may be applied to
$\langle \langle {\mathbf {f}}, -\rangle \rangle $
may be applied to
![]() $\mathbf {I}^{\mathrm {ord}, \curlyvee }(\phi ^{p\infty })$
, thanks to Lemma 2.3.
$\mathbf {I}^{\mathrm {ord}, \curlyvee }(\phi ^{p\infty })$
, thanks to Lemma 2.3.
Proposition 4.10 The collection
of meromorphic functions on
![]() $\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}$
has the following properties.
$\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}$
has the following properties.
-
(1) Let
 $(x, y)\in \mathscr {X}^{\mathrm {cl}}_{\mathbf {Q}_{p}^{\mathrm {ab}} /\mathbf {Q}_{p}^{\mathrm {ab}}}(\mathbf {C})$
have contracted weight
$(x, y)\in \mathscr {X}^{\mathrm {cl}}_{\mathbf {Q}_{p}^{\mathrm {ab}} /\mathbf {Q}_{p}^{\mathrm {ab}}}(\mathbf {C})$
have contracted weight
 $(k_{0}, w, l)$
satisfying (4.5.5)If
$(k_{0}, w, l)$
satisfying (4.5.5)If $$ \begin{align}\begin{aligned} | l_{\tau}| \leq w_{\tau}-2, \qquad |k_{0}|\leq w_{\tau} - 2- | l_{\tau} |. \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} | l_{\tau}| \leq w_{\tau}-2, \qquad |k_{0}|\leq w_{\tau} - 2- | l_{\tau} |. \end{aligned}\end{align} $$
 $(x, y)$
is outside the polar locus of
$(x, y)$
is outside the polar locus of
 $\mathscr {L}_{p}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })$
, we have (4.5.6)where
$\mathscr {L}_{p}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })$
, we have (4.5.6)where $$ \begin{align}\begin{aligned} \mathscr{L}_{p}(\mathscr{V},\mathbf{f}, \phi^{p\infty})( x, y) = e_{p\infty}(V_{(\pi, \chi)}) \cdot \mathscr{L}(V_{(\pi, \chi)}, 0),\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \mathscr{L}_{p}(\mathscr{V},\mathbf{f}, \phi^{p\infty})( x, y) = e_{p\infty}(V_{(\pi, \chi)}) \cdot \mathscr{L}(V_{(\pi, \chi)}, 0),\end{aligned}\end{align} $$
 $\pi =\pi _{x}$
,
$\pi =\pi _{x}$
,
 $\chi =\chi _{y}$
.
$\chi =\chi _{y}$
.
-
(2) For each
 $(x, y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
, there is a pair
$(x, y)\in \mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
, there is a pair
 $(\mathbf {f}, \phi ^{p\infty })\in \mathcal {A}$
such that
$(\mathbf {f}, \phi ^{p\infty })\in \mathcal {A}$
such that
 $\mathscr {L}_{p}(\mathscr {V},\mathbf {f}, \phi ^{p\infty })$
does not have a pole at
$\mathscr {L}_{p}(\mathscr {V},\mathbf {f}, \phi ^{p\infty })$
does not have a pole at
 $(x, y)$
.
$(x, y)$
.
Note that the right-hand side of (4.5.6) is the same as in (1.1.8) and independent of
![]() $(\mathbf {f}, \phi ^{p\infty })$
. This will enable us to glue the various
$(\mathbf {f}, \phi ^{p\infty })$
. This will enable us to glue the various
![]() $\mathscr {L}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })$
into the sought-for p-adic L-function.
$\mathscr {L}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })$
into the sought-for p-adic L-function.
Proof The second statement follows from Lemma 4.4.
It remains to prove the interpolation property. Abbreviate
![]() $\mathscr {L}_{p}=\mathscr {L}_{p}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })$
, and let
$\mathscr {L}_{p}=\mathscr {L}_{p}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })$
, and let
![]() $\overline {W}_{v}:=\overline {\mathbf {W}}_{\mathbf {f}|x}$
,
$\overline {W}_{v}:=\overline {\mathbf {W}}_{\mathbf {f}|x}$
,
![]() $\alpha =\alpha _{\pi }$
. Denote by
$\alpha =\alpha _{\pi }$
. Denote by
![]() $(x_{0}, y_{0})\in \mathscr {X}^{\mathrm {cl}}$
and
$(x_{0}, y_{0})\in \mathscr {X}^{\mathrm {cl}}$
and
![]() $\iota \colon \mathbf {Q}_{p}^{\mathrm {ab}}(x_{0}, y_{0})\hookrightarrow \mathbf {C}$
the data corresponding to
$\iota \colon \mathbf {Q}_{p}^{\mathrm {ab}}(x_{0}, y_{0})\hookrightarrow \mathbf {C}$
the data corresponding to
![]() $(x, y)$
. Let
$(x, y)$
. Let
![]() $k_{x,y}$
and
$k_{x,y}$
and
![]() $\xi _{x,y}$
(respectively,
$\xi _{x,y}$
(respectively,
![]() $k_{x_{0}, y_{0}}$
,
$k_{x_{0}, y_{0}}$
,
![]() $\xi _{x_{0}, y_{0}}$
,
$\xi _{x_{0}, y_{0}}$
,
![]() $\underline {\kappa }_{2}=\underline {\kappa }_{2, x_{0}, y_{0}}$
) be defined by (4.2.1) (respectively, by the analogous formulas for the objects attached to
$\underline {\kappa }_{2}=\underline {\kappa }_{2, x_{0}, y_{0}}$
) be defined by (4.2.1) (respectively, by the analogous formulas for the objects attached to
![]() $(x_{0},y_{0})$
instead of
$(x_{0},y_{0})$
instead of
![]() $(x,y)$
).
$(x,y)$
).
By the definitions and the defining property of
![]() $\langle \langle \, , \, \rangle \rangle $
in Proposition 4.2, and of
$\langle \langle \, , \, \rangle \rangle $
in Proposition 4.2, and of
![]() $\mathbf {R}_{v}$
in Proposition 4.7, we have
$\mathbf {R}_{v}$
in Proposition 4.7, we have
 $$ \begin{align*}&\mathscr{L}_{p}(x, y) = C\cdot {\iota\langle \mathbf{f}_{x_{0}}, e^{\mathrm{ord}} \mathrm{I}(\phi^{p\infty}; \chi_{y_{0}}, \xi_{x_{0}, y_{0}}, k_{x_{0}, y_{0}}\rangle \over \prod_{v\in S} R_{v}^{\natural}( \iota \overline W_{v}, \phi_{v},\chi_{v})}\\ &\quad = C\cdot {|D_{F}|^{1/2}\zeta_{F}(2) \cdot |D_{F}| |D_{E}|^{1/2} \over \omega_{x, p}^{}(-1)\cdot e_{p}( \mathrm{ad}(V_{\pi})(1)) \cdot 2^{\sum_{v\vert\infty} -1-w_{v}}} \cdot {q_{F, p}^{r}\alpha_{\pi}^{-r}(\mathbf{f}_{x}^{\mathrm{a}}, w_{r,p}^{-1}I_{r}(\phi^{p\infty}; \chi,\xi_{x, y} , \kappa_{2}', k_{x, y}) \over L(1, \pi^{}, \mathrm{ad}) \cdot \prod_{v\in S} R_{v}^{\natural}( \iota \overline W_{v}, \phi_{v},\chi_{v})},\end{align*} $$
$$ \begin{align*}&\mathscr{L}_{p}(x, y) = C\cdot {\iota\langle \mathbf{f}_{x_{0}}, e^{\mathrm{ord}} \mathrm{I}(\phi^{p\infty}; \chi_{y_{0}}, \xi_{x_{0}, y_{0}}, k_{x_{0}, y_{0}}\rangle \over \prod_{v\in S} R_{v}^{\natural}( \iota \overline W_{v}, \phi_{v},\chi_{v})}\\ &\quad = C\cdot {|D_{F}|^{1/2}\zeta_{F}(2) \cdot |D_{F}| |D_{E}|^{1/2} \over \omega_{x, p}^{}(-1)\cdot e_{p}( \mathrm{ad}(V_{\pi})(1)) \cdot 2^{\sum_{v\vert\infty} -1-w_{v}}} \cdot {q_{F, p}^{r}\alpha_{\pi}^{-r}(\mathbf{f}_{x}^{\mathrm{a}}, w_{r,p}^{-1}I_{r}(\phi^{p\infty}; \chi,\xi_{x, y} , \kappa_{2}', k_{x, y}) \over L(1, \pi^{}, \mathrm{ad}) \cdot \prod_{v\in S} R_{v}^{\natural}( \iota \overline W_{v}, \phi_{v},\chi_{v})},\end{align*} $$
where
![]() $r\in (\mathbf {Z}_{\geq 1})^{S_{p}}$
is sufficiently large, and the second equality follows from the interpolation properties of
$r\in (\mathbf {Z}_{\geq 1})^{S_{p}}$
is sufficiently large, and the second equality follows from the interpolation properties of
![]() $\mathbf { I}^{\mathrm {ord}, \curlyvee }$
in (3.4.11), and of
$\mathbf { I}^{\mathrm {ord}, \curlyvee }$
in (3.4.11), and of
![]() $\langle \ , \ \rangle $
in Lemma 4.1.
$\langle \ , \ \rangle $
in Lemma 4.1.
Using first Waldspurger’s integral representation as in Proposition 4.3, and then the calculations of local integrals in Lemmas 4.5 and 4.6, we find
 $$ \begin{align*}\mathscr{L}_{p}(x, y) &= C\cdot {\prod_{v\vert p} R_{r,v}^{\dagger}(\overline W_{v}, \chi_{v}, \alpha_{v}) \over 2^{\sum_{\tau}-1- w_{\tau}} \omega_{x,p}^{}(-1)\cdot e_{p}(\mathrm{ad}(V_{\pi})(1))} \cdot {|D_{F}|^{1/2} L(1/2, \pi_{E}\otimes \chi)\over L(1,\eta) L(1, \pi,\mathrm{ad})} \prod_{v\vert \infty} R_{v}^{\dagger}( \overline W_{v},\chi_{v}, k_{v}) \\ &= C\cdot i^{-k_{0}[F:\mathbf{Q}]} { \omega_{x,p}^{}\omega_{y, p}^{\mathrm{sm}}(-1)}{ e_{p}(V_{\pi_{E}\otimes\chi}) \over L(1, \eta_{p})\cdot e_{p}(\mathrm{ad}(V_{\pi})(1))} \cdot {|D_{F}|^{1/2} L(1/2, \pi_{E}\otimes \chi)\over L(1,\eta) L(1, \pi,\mathrm{ad})}. \\ &= i^{k_{0}[F:\mathbf{Q}]} \cdot { e_{p}(V_{(\pi, \chi)})} \cdot \mathscr{L}(V_{(\pi, \chi)}, 0), \end{align*} $$
$$ \begin{align*}\mathscr{L}_{p}(x, y) &= C\cdot {\prod_{v\vert p} R_{r,v}^{\dagger}(\overline W_{v}, \chi_{v}, \alpha_{v}) \over 2^{\sum_{\tau}-1- w_{\tau}} \omega_{x,p}^{}(-1)\cdot e_{p}(\mathrm{ad}(V_{\pi})(1))} \cdot {|D_{F}|^{1/2} L(1/2, \pi_{E}\otimes \chi)\over L(1,\eta) L(1, \pi,\mathrm{ad})} \prod_{v\vert \infty} R_{v}^{\dagger}( \overline W_{v},\chi_{v}, k_{v}) \\ &= C\cdot i^{-k_{0}[F:\mathbf{Q}]} { \omega_{x,p}^{}\omega_{y, p}^{\mathrm{sm}}(-1)}{ e_{p}(V_{\pi_{E}\otimes\chi}) \over L(1, \eta_{p})\cdot e_{p}(\mathrm{ad}(V_{\pi})(1))} \cdot {|D_{F}|^{1/2} L(1/2, \pi_{E}\otimes \chi)\over L(1,\eta) L(1, \pi,\mathrm{ad})}. \\ &= i^{k_{0}[F:\mathbf{Q}]} \cdot { e_{p}(V_{(\pi, \chi)})} \cdot \mathscr{L}(V_{(\pi, \chi)}, 0), \end{align*} $$
as desired.
Remark 4.11 The interpolation factors
![]() $e_{p\infty }(V_{(\pi , \chi )})$
are easily seen to agree with the predictions of Coates and Perrin-Riou (see [Reference CoatesCoa91]) for a (cyclotomic) p-adic L-function attached to the “virtual motive” (1.1.3), up to a subtlety that we now explain. With the notation used in (1.1.4), for
$e_{p\infty }(V_{(\pi , \chi )})$
are easily seen to agree with the predictions of Coates and Perrin-Riou (see [Reference CoatesCoa91]) for a (cyclotomic) p-adic L-function attached to the “virtual motive” (1.1.3), up to a subtlety that we now explain. With the notation used in (1.1.4), for
![]() $v\vert p$
, consider the
$v\vert p$
, consider the
![]() $G_{F_{v}}$
-representations
$G_{F_{v}}$
-representations
 $$ \begin{align*} \mathrm{ad}(V_{\pi,v})(1)&:=\mathrm{End}\,^{0}(V_{\pi})(1)\\&\quad\supset \mathrm{ad}(V_{\pi,v})(1)^{+}:= \mathrm{Ker}\, [\mathrm{ad}(V_{\pi})(1)\to \mathrm{Hom}\,(V_{\pi,v}^{+}, V_{\pi,v}^{-})(1)]\\ &\quad\supset \mathrm{ad}(V_{\pi,v})(1)^{++} =\mathrm{Hom}\,(V_{\pi,v}^{-}, V_{\pi,v}^{+})(1)), \end{align*} $$
$$ \begin{align*} \mathrm{ad}(V_{\pi,v})(1)&:=\mathrm{End}\,^{0}(V_{\pi})(1)\\&\quad\supset \mathrm{ad}(V_{\pi,v})(1)^{+}:= \mathrm{Ker}\, [\mathrm{ad}(V_{\pi})(1)\to \mathrm{Hom}\,(V_{\pi,v}^{+}, V_{\pi,v}^{-})(1)]\\ &\quad\supset \mathrm{ad}(V_{\pi,v})(1)^{++} =\mathrm{Hom}\,(V_{\pi,v}^{-}, V_{\pi,v}^{+})(1)), \end{align*} $$
where “
![]() $0$
” denotes trace-
$0$
” denotes trace-
![]() $0$
elements, and the cokernel of the second containment is isomorphic to the cyclotomic character. Then (1.1.4) differs from the ratio of the v-adic Coates–Perrin-Riou factors for the hypothetical L-functions of
$0$
elements, and the cokernel of the second containment is isomorphic to the cyclotomic character. Then (1.1.4) differs from the ratio of the v-adic Coates–Perrin-Riou factors for the hypothetical L-functions of
![]() $V_{\pi } \otimes \mathrm { Ind}_{G_{F}}^{G_{E}}{V_{\chi }}$
and of
$V_{\pi } \otimes \mathrm { Ind}_{G_{F}}^{G_{E}}{V_{\chi }}$
and of
![]() $\mathrm {ad}(V_{\pi })(1)$
by the appearance of
$\mathrm {ad}(V_{\pi })(1)$
by the appearance of
![]() $\gamma (\iota \mathrm {ad}(V_{\pi ,v})(1)^{++}, \psi _{v})^{-1}$
in place of
$\gamma (\iota \mathrm {ad}(V_{\pi ,v})(1)^{++}, \psi _{v})^{-1}$
in place of
![]() $\gamma (\iota \mathrm {ad}(V_{\pi ,v})(1)^{+}, \psi _{v})^{-1}$
. This discrepancy removes the trivial zero
$\gamma (\iota \mathrm {ad}(V_{\pi ,v})(1)^{+}, \psi _{v})^{-1}$
. This discrepancy removes the trivial zero
![]() $\gamma (\mathbf {C}(1), \psi _{v})^{-1}$
from the latter inverse gamma factor.
$\gamma (\mathbf {C}(1), \psi _{v})^{-1}$
from the latter inverse gamma factor.
4.5.3 Rationality and completion of the proof of Theorem A
By Proposition 4.10 and the density of classical points, the functions
![]() $\mathscr {L}_{p}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })=(4.5.4)\in \mathscr {K}(\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}})$
glue to a function
$\mathscr {L}_{p}(\mathscr {V}, \mathbf {f}, \phi ^{p\infty })=(4.5.4)\in \mathscr {K}(\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}})$
glue to a function
which satisfies the required interpolation property, and whose polar locus does not meet the set
![]() $\mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
. All that is left to show is that
$\mathscr {X}^{\mathrm {cl}, \mathrm {sd}}$
. All that is left to show is that
![]() $\mathscr {L}_{p}(\mathscr {V})$
descends to
$\mathscr {L}_{p}(\mathscr {V})$
descends to
![]() $\mathscr {K}(\mathscr {X})$
. It will be a consequence of the following.
$\mathscr {K}(\mathscr {X})$
. It will be a consequence of the following.
Proposition 4.12 Let
![]() $\mathscr {X}^{\mathrm {cl}, \parallel } \subset \mathscr {X}^{\mathrm {cl}}$
be the sub-ind-scheme of those
$\mathscr {X}^{\mathrm {cl}, \parallel } \subset \mathscr {X}^{\mathrm {cl}}$
be the sub-ind-scheme of those
![]() $(x, y)$
corresponding to a representation
$(x, y)$
corresponding to a representation
![]() $\pi \boxtimes \chi $
whose contracted weight
$\pi \boxtimes \chi $
whose contracted weight
![]() $(k_{0}, w, l)$
satisfies (
4.5.5
) and is parallel.Footnote
11
There is a function
$(k_{0}, w, l)$
satisfies (
4.5.5
) and is parallel.Footnote
11
There is a function
such that for any
![]() $z=(x, y) \in \mathscr {X}^{\mathrm {cl}, \parallel }(\mathbf {C})$
corresponding to a point
$z=(x, y) \in \mathscr {X}^{\mathrm {cl}, \parallel }(\mathbf {C})$
corresponding to a point
![]() $z_{0}\in \mathscr {X}^{\mathrm {cl},||}$
and an embedding
$z_{0}\in \mathscr {X}^{\mathrm {cl},||}$
and an embedding
![]() $\iota \colon \mathbf {Q}_{p}(z_{0})\hookrightarrow \mathbf {C}$
, with attached representation
$\iota \colon \mathbf {Q}_{p}(z_{0})\hookrightarrow \mathbf {C}$
, with attached representation
![]() $\pi \boxtimes \chi $
, we have
$\pi \boxtimes \chi $
, we have
 $$ \begin{align}\quad\qquad \mathrm{L}(z)=\iota\mathrm{L}(z_{0}) = i^{-(1+k_{0})[F:\mathbf{Q}]} \gamma(1, \eta^{\infty}\omega^{\infty}, \psi^{\infty})^{-1} {\zeta_{F}(2) L(1/2, \pi_{E}\otimes \chi)\over \pi^{[F:\mathbf{Q}]} L(1, \pi, \mathrm{ad})}. \end{align} $$
$$ \begin{align}\quad\qquad \mathrm{L}(z)=\iota\mathrm{L}(z_{0}) = i^{-(1+k_{0})[F:\mathbf{Q}]} \gamma(1, \eta^{\infty}\omega^{\infty}, \psi^{\infty})^{-1} {\zeta_{F}(2) L(1/2, \pi_{E}\otimes \chi)\over \pi^{[F:\mathbf{Q}]} L(1, \pi, \mathrm{ad})}. \end{align} $$
Here, we denote by
![]() $\omega _{\pi }$
the central character of
$\omega _{\pi }$
the central character of
![]() $\pi $
, set
$\pi $
, set
![]() $\omega _{\chi }:=\chi _{|\mathbf {A}^{\times }}$
$\omega _{\chi }:=\chi _{|\mathbf {A}^{\times }}$
![]() $\omega =\omega _{\pi }\omega _{\chi }$
, and define
$\omega =\omega _{\pi }\omega _{\chi }$
, and define
![]() $\gamma (s,\omega ^{\prime \infty }, \psi ^{\infty }) := \prod _{v\nmid \infty } \gamma (s,\omega ^{\prime }_{v}, \psi _{v})$
.
$\gamma (s,\omega ^{\prime \infty }, \psi ^{\infty }) := \prod _{v\nmid \infty } \gamma (s,\omega ^{\prime }_{v}, \psi _{v})$
.
Remark 4.13 The construction of this paper gives an alternative proof of this result. However, due to the occurrence of the additive character
![]() $\psi $
in the definition of the form I (via the Weil representation), keeping track of rationality requires some burdensome bookkeeping.
$\psi $
in the definition of the form I (via the Weil representation), keeping track of rationality requires some burdensome bookkeeping.
Proof This is a consequence of a well-known algebraicity theorem of Shimura [Reference ShimuraShi78, Theorem 4.2], applied to the newform in the representation
![]() $\pi $
and the CM form attached to
$\pi $
and the CM form attached to
![]() $\chi $
, whose central character is
$\chi $
, whose central character is
![]() $\eta \omega _{\chi }$
. (For the comparison of Shimura’s periods and adjoint L-values, see [Reference Cai and FanCST14, Proposition 1.11].)
$\eta \omega _{\chi }$
. (For the comparison of Shimura’s periods and adjoint L-values, see [Reference Cai and FanCST14, Proposition 1.11].)
Corollary 4.14 The function
![]() $\mathscr {L}_{p}(\mathscr {V})$
belongs to
$\mathscr {L}_{p}(\mathscr {V})$
belongs to
![]() $\mathscr {K}(\mathscr {X}) \subset \mathscr {K}(\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}})$
.
$\mathscr {K}(\mathscr {X}) \subset \mathscr {K}(\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}})$
.
Proof We need to show that
for all
![]() $\sigma \in \mathrm {Gal}(\mathbf {Q}_{p}^{\mathrm {ab}}/\mathbf {Q}_{p})$
. Let
$\sigma \in \mathrm {Gal}(\mathbf {Q}_{p}^{\mathrm {ab}}/\mathbf {Q}_{p})$
. Let
![]() $\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}, \parallel , \mathrm {reg}}$
be the intersection of
$\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}, \parallel , \mathrm {reg}}$
be the intersection of
![]() $\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}, \parallel } $
with the complement of the polar locus of
$\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}, \parallel } $
with the complement of the polar locus of
![]() $\mathscr {L}_{p}(\mathscr {V})$
. Since this set is dense in
$\mathscr {L}_{p}(\mathscr {V})$
. Since this set is dense in
![]() $\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}$
, it suffices to show that (4.5.8) holds for the restriction
$\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}$
, it suffices to show that (4.5.8) holds for the restriction
![]() $\mathrm { L}_{p}(\mathscr {V})$
of
$\mathrm { L}_{p}(\mathscr {V})$
of
![]() $\mathscr {L}_{p}(\mathscr {V})$
to
$\mathscr {L}_{p}(\mathscr {V})$
to
![]() ${\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}, \parallel , \mathrm {reg}}}$
; in other words, that
${\mathscr {X}_{\mathbf {Q}_{p}^{\mathrm {ab}}}^{\mathrm {cl}, \parallel , \mathrm {reg}}}$
; in other words, that
![]() $\mathrm {L}_{p}(\mathscr {V})$
belongs to
$\mathrm {L}_{p}(\mathscr {V})$
belongs to
![]() $\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel , \mathrm {reg}})$
.
$\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel , \mathrm {reg}})$
.
 $$ \begin{align*}\mathrm{L}_{p}(\mathscr{V})(z) &= {i^{[F:\mathbf{Q}]}\gamma(1,\eta^{\infty}, \psi^{\infty}) \over {L(1, \eta)}} \cdot { \gamma(1, \eta^{\infty}\omega^{\infty}, \psi^{\infty})\over \gamma(1, \eta^{\infty}, \psi^{\infty}) \gamma(1, \omega^{\infty}, \psi^{\infty})}\cdot {1\over \gamma(1, \omega^{p\infty}, \psi^{p\infty})^{-1}} \\&\quad\cdot {e_{p}(V_{(x, y)}) \over \gamma(1, \omega_{p}, \psi_{p})^{-1}} \cdot \mathrm{L}(z).\end{align*} $$
$$ \begin{align*}\mathrm{L}_{p}(\mathscr{V})(z) &= {i^{[F:\mathbf{Q}]}\gamma(1,\eta^{\infty}, \psi^{\infty}) \over {L(1, \eta)}} \cdot { \gamma(1, \eta^{\infty}\omega^{\infty}, \psi^{\infty})\over \gamma(1, \eta^{\infty}, \psi^{\infty}) \gamma(1, \omega^{\infty}, \psi^{\infty})}\cdot {1\over \gamma(1, \omega^{p\infty}, \psi^{p\infty})^{-1}} \\&\quad\cdot {e_{p}(V_{(x, y)}) \over \gamma(1, \omega_{p}, \psi_{p})^{-1}} \cdot \mathrm{L}(z).\end{align*} $$
We show that all factors belong to
![]() $\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel , \mathrm {reg}})$
:
$\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel , \mathrm {reg}})$
:
-
• By the class number formula and standard results on Gauß sums, the ratio
 $ {L(1, \eta )/ i^{[F:\mathbf {Q}]} \gamma (1,\eta ^{\infty })} $
is rational, as both numerator and denominator are rational multiples of
$ {L(1, \eta )/ i^{[F:\mathbf {Q}]} \gamma (1,\eta ^{\infty })} $
is rational, as both numerator and denominator are rational multiples of
 $|D_{E/F}|^{-1/2}$
.
$|D_{E/F}|^{-1/2}$
. -
• By (4.0.1), the second and fourth ratios are values of functions on
 $\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel })$
, as
$\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel })$
, as
 $e_{p}(V_{(x, y)})$
is a ratio of inverse gamma factors of characters whose ratio is
$e_{p}(V_{(x, y)})$
is a ratio of inverse gamma factors of characters whose ratio is
 $\omega _{p}$
.
$\omega _{p}$
. -
• As
 $\mathscr {X}$
is connected and it contains points z with
$\mathscr {X}$
is connected and it contains points z with
 $\omega _{z}=\mathbf {1}$
, the character
$\omega _{z}=\mathbf {1}$
, the character
 $\omega _{z,v}$
is unramified for all
$\omega _{z,v}$
is unramified for all
 $z\in \mathscr {X}$
and all
$z\in \mathscr {X}$
and all
 $v\nmid p$
; thus, for those v, the quantity
$v\nmid p$
; thus, for those v, the quantity
 $\gamma (\omega _{v})$
is a ratio of L-values, and hence the third factor is also the value of a function in
$\gamma (\omega _{v})$
is a ratio of L-values, and hence the third factor is also the value of a function in
 $\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel })$
.
$\mathscr {O}(\mathscr {X}^{\mathrm {cl}, \parallel })$
. -
• Finally,
 $\mathrm {L}\in \mathscr {O}(\mathscr {X}^{\mathrm {cl},\parallel })$
by Proposition 4.12.
$\mathrm {L}\in \mathscr {O}(\mathscr {X}^{\mathrm {cl},\parallel })$
by Proposition 4.12.
This completes the proof of the corollary and of Theorem A.
A Reality shows and double-factorial identities
Consider the identity
 $$ \begin{align*}\begin{aligned} (*)\qquad \sum_{k=0}^{n} {n \choose k} (2k-1)!! (2n-2k-1)!! = 2^n n!,\end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} (*)\qquad \sum_{k=0}^{n} {n \choose k} (2k-1)!! (2n-2k-1)!! = 2^n n!,\end{aligned}\end{align*} $$
where we recall that
![]() $(2m-1)!! = 1 \cdot 3 \cdot 5 \cdots (2m-1)$
is the number of perfect matchings (into pairs) of a
$(2m-1)!! = 1 \cdot 3 \cdot 5 \cdots (2m-1)$
is the number of perfect matchings (into pairs) of a
![]() $2m$
-element set. Since
$2m$
-element set. Since
![]() $\Gamma (j+1/2) = {(2j-1)!! \over 2^{j}}\sqrt {\pi }$
, the identity
$\Gamma (j+1/2) = {(2j-1)!! \over 2^{j}}\sqrt {\pi }$
, the identity
![]() $(*)$
is equivalent to (3.3.9).
$(*)$
is equivalent to (3.3.9).
Quick analytic proofs of
![]() $(*)$
have appeared in [Reference Andersen and AbelAA10] and [Reference Gould and QuaintanceGQ12, Theorem 3]. As we were not able to find a bijective proof in the literature, we give one here. Another bijective proof was communicated to the author by David Callan.
$(*)$
have appeared in [Reference Andersen and AbelAA10] and [Reference Gould and QuaintanceGQ12, Theorem 3]. As we were not able to find a bijective proof in the literature, we give one here. Another bijective proof was communicated to the author by David Callan.
A reality TV show format is an algorithm whose inputs are called players’ choices and whose outputs are called outcomes (the set of players is partitioned into two disjoint sets, the producers and the participants). A format is said to be bijective if its set of players’ choices is in bijection with its set of outcomes.
We will describe two bijective formats for reality TV shows, with different sets of players’ choices but the same set of outcomes. In each case, there are
![]() $2n$
participants forming an ordered set of n heterosexual couplesFootnote
12
; there are two tropical islands, Q and H, and in each case, the outcome is:
$2n$
participants forming an ordered set of n heterosexual couplesFootnote
12
; there are two tropical islands, Q and H, and in each case, the outcome is:
-
• a new matching of the participants into n disjoint couples (which may be homosexual or heterosexual), and
-
• an assignment of each participant to either island Q or island H, such that
-
• each person lives in the same island as both their old and their new partners.
-
Show 1. The producers choose a set of couples, send all their members to island Q, and send all the other participants to island H. Within each island, people mingle until they form new disjoint couples (heterosexual or homosexual) as they wish.
-
Show 2. The producers pick a permutation
 $\sigma \colon \{1, \ldots , n\} \to \{1, \ldots , n\} $
, then they do the following.
$\sigma \colon \{1, \ldots , n\} \to \{1, \ldots , n\} $
, then they do the following.-
• Initialize:
 $i=1$
and the set variable
$i=1$
and the set variable
 $C= \emptyset $
(where C is for “cycle”; to be thought of as the set of couples embarked in the show’s boat at a given time).
$C= \emptyset $
(where C is for “cycle”; to be thought of as the set of couples embarked in the show’s boat at a given time). -
• Process:
-
(a) Consider couple i, set
 $C_{\mathrm {new}}=C_{\mathrm {old}}\cup \{i\}$
, and interview couple member
$C_{\mathrm {new}}=C_{\mathrm {old}}\cup \{i\}$
, and interview couple member
 $p_i$
where: if
$p_i$
where: if
 $C=\{i\}$
, then
$C=\{i\}$
, then
 $p_i$
is the woman; if
$p_i$
is the woman; if
 $C\supsetneq \{i\}$
, then
$C\supsetneq \{i\}$
, then
 $p_i$
is the one that does not yet have a new partner.
$p_i$
is the one that does not yet have a new partner.The possible answers to the interview question are “H” and “Q”.
-
(b) If
 $j = \sigma (i) \notin C$
and
$j = \sigma (i) \notin C$
and
 $p_i$
responds H (resp. Q):
$p_i$
responds H (resp. Q):-
– rematch
 $p_i$
with the person of opposite (respectively, the same) sex of couple
$p_i$
with the person of opposite (respectively, the same) sex of couple
 $j=\sigma (i)$
. Set
$j=\sigma (i)$
. Set
 $i_{\mathrm {new}} = j$
. Return to (a).
$i_{\mathrm {new}} = j$
. Return to (a).
-
-
(c) If
 $j = \sigma (i) \in C $
and
$j = \sigma (i) \in C $
and
 $p_i$
responds
$p_i$
responds
 $H $
(resp. Q):
$H $
(resp. Q):-
– rematch
 $p_i $
with the unique nonrematched person of couple j, and send all members of the “original couples” in C to island H (respectively, Q); set
$p_i $
with the unique nonrematched person of couple j, and send all members of the “original couples” in C to island H (respectively, Q); set
 $C_{\mathrm {new}}=\emptyset $
;
$C_{\mathrm {new}}=\emptyset $
; -
– if everyone has been rematched, STOP. Else: set
 $i_{\mathrm {new}}\in \{1, \ldots , n\}$
to be the smallest such that neither member of couple
$i_{\mathrm {new}}\in \{1, \ldots , n\}$
to be the smallest such that neither member of couple
 $i_{\mathrm {new}}$
has been rematched. Return to (a).
$i_{\mathrm {new}}$
has been rematched. Return to (a).
-
-
-
Proof of
 $(*)$
$(*)$
The number of possible players’ choices in Show 1 is the left-hand side of
![]() $(*)$
. The number of possible players’ choices in Show 2 is the right-hand side of
$(*)$
. The number of possible players’ choices in Show 2 is the right-hand side of
![]() $(*)$
. However, the shows are bijective with the same set of outcomes.
$(*)$
. However, the shows are bijective with the same set of outcomes.
B Errata to [Reference DisegniDis20]
The conclusions of the statements of Lemma 5.2.2 and Propositions 5.2.3 and 5.2.4 should, respectively, have
![]() $A[T^{\pm 1}]$
,
$A[T^{\pm 1}]$
,
![]() $\mathscr {O}_{X}[T^{\pm 1}]$
, and
$\mathscr {O}_{X}[T^{\pm 1}]$
, and
![]() $\mathscr {O}_{X}[T^{\pm 1}]$
instead of
$\mathscr {O}_{X}[T^{\pm 1}]$
instead of
![]() $A[T]$
,
$A[T]$
,
![]() $\mathscr {O}_{X}[T]$
, and
$\mathscr {O}_{X}[T]$
, and
![]() $\mathscr {O}_{X}[T]$
.
$\mathscr {O}_{X}[T]$
.
Acknowledgment
I am grateful to David Callan, Haruzo Hida, Ming-Lun Hsieh, and Xinyi Yuan for useful correspondence, and to the referees for a very careful reading.