Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T09:57:45.940Z Has data issue: false hasContentIssue false
  • English
  • Français

p-adic L-functions and the Rationality of Darmon Cycles

Published online by Cambridge University Press:  20 November 2018

Marco Adamo Seveso
Marco Adamo Seveso*
Affiliation:
Dipartimento di Matematica Federigo Enriques, Università degli studi di Milano email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Darmon cycles are a higher weight analogue of Stark–Heegner points. They yield local cohomology classes in the Deligne representation associated with a cuspidal form on 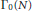${{\Gamma }_{0}}\left( N \right)$ of even weight 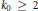${{k}_{0}}\,\ge \,2$. They are conjectured to be the restriction of global cohomology classes in the Bloch–Kato Selmer group defined over narrow ring class fields attached to a real quadratic field. We show that suitable linear combinations of them obtained by genus characters satisfy these conjectures. We also prove 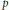$p$-adic Gross–Zagier type formulas, relating the derivatives of 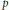$p$-adic $L$-functions of the weight variable attached to imaginary (resp. real) quadratic fields to Heegner cycles (resp. Darmon cycles). Finally we express the second derivative of the Mazur– Kitagawa 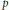$p$-adic $L$-function of the weight variable in terms of a global cycle defined over a quadratic extension of 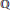$\mathbb{Q}$.

Keywords

11F6714G05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 5 , 01 October 2012 , pp. 1122 - 1181
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bertolini, M. and Darmon, H., Heegner points on Mumford-Tate curves. Invent. Math. 126(1996), no. 3, 413–456. http://dx.doi.org/10.1007/s002220050105 Google Scholar
[2] Bertolini, M. and Darmon, H., Hida families and rational points on elliptic curves. Invent. Math. 168(2007), no. 2, 371–431. http://dx.doi.org/10.1007/s00222-007-0035-4 Google Scholar
[3] Bertolini, M. and Darmon, H., The rationality of Stark-Heegner points over genus fields of real quadratic fields. Ann. of Math. 170(2009), no. 1, 343–370. http://dx.doi.org/10.4007/annals.2009.170.343 Google Scholar
[4] Bertolini, M., Darmon, H., and Iovita, A., Families of automorphic forms on definite quaternion algebras and Teitelbaum's conjecture. Astérisque, to appear.Google Scholar
[5] Bertolini, M., Darmon, H., Iovita, A., and Spiess, M., Teitelbaum's exceptional zero conjecture in the anticyclotomic setting. Amer. J. Math. 124(2002), no. 2, 411–449. http://dx.doi.org/10.1353/ajm.2002.0009 Google Scholar
[6] Bertolini, M., Darmon, H., and Green, P., Periods and points attached to quadratic algebras. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ., 49, Cambridge University Press, Cambridge, MA, 2004, pp. 323–367.Google Scholar
[7] Chenevier, G., Une correspondance de Jaquet-Langlands p-adique. Duke Math. J. 126(2005), no. 3, 161–194. http://dx.doi.org/10.1215/S0012-7094-04-12615-6 Google Scholar
[8] Coleman, R. F., p-adic Banach spaces and families of modular forms. Invent. Math. 127(1997), no. 3, 417–479. http://dx.doi.org/10.1007/s002220050127 Google Scholar
[9] Colmez, P., Invariants Let dérivées de valeurs propres de Frobenius. Astérisque 331(2010), 13–28.Google Scholar
[10] Darmon, H., Integration onHp ×Hand arithmetic applications. Ann. of Math. 154(2001), no. 3, 589–639. http://dx.doi.org/10.2307/3062142 Google Scholar
[11] Dasgupta, S., Stark-Heegner points on modular Jacobians. Ann. Scient. École Norm. Sup. (4) 38(2005), no. 3, 427–469.Google Scholar
[12] Dasgupta, S. and Teitelbaum, J., The p-adic upper half plane. In: p-adic geometry. Univ. Lecture Ser., 45, American Mathematical Society, Providence, RI, 2008, pp. 65–121.Google Scholar
[13] Greenberg, M., Stark-Heegner points and the cohomology of quaternionic Shimura varieties. Duke Math. J. 147(2009), no. 3, 541–575. http://dx.doi.org/10.1215/00127094-2009-017 Google Scholar
[14] Hida, H., Elementary theory of L-functions and Eisenstein series. London Mathematical Society Student Texts, 26, Cambridge University Press, Cambridge, 1993.Google Scholar
[15] Iovita, A. and M. Spieß, Derivatives of p-adic L-functions, Heegner cycles and monodromy modules attached to modular forms. Invent. Math. 154(2003), no. 2, 333–384. http://dx.doi.org/10.1007/s00222-003-0306-7 Google Scholar
[16] Kato, K., p-adic Hodge theory and values of zeta functions of modular forms. Cohomologies p-adiques et applications arithmétiques. III. Astérisque 295(2004), ix, 117–290.Google Scholar
[17] Nekovář, J., Kolyvagin's method for Chow groups of Kuga-Sato varieties. Invent. Math. 107(1992), no. 1, 99–125. http://dx.doi.org/10.1007/BF01231883 Google Scholar
[18] Nekovář, J., The Euler system method for CM-points on Shimura curves. In: L-functions and Galois representations, London Math. Soc. Lecture Note Ser., 320, Cambridge University Press, Cambridge, 2007, pp. 471–547.Google Scholar
[19] Orton, L., An elementary proof of a weak exceptional zero conjecture. Canad. J.Math. 56(2004), no. 2, 373–405. http://dx.doi.org/10.4153/CJM-2004-018-4 Google Scholar
[20] Popa, A., Central values of Rankin L-series over real quadratic fields. Compos. Math. 142(2006), no. 4, 811–866. http://dx.doi.org/10.1112/S0010437X06002259 Google Scholar
[21] Mazur, B., Tate, J., and Teitelbaum, J., On p-adic analogues of the conjectures of Birch and Swinnerton-Dyer. Invent. Math. 84(1986), no. 1, 1–48. (1986). http://dx.doi.org/10.1007/BF01388731 Google Scholar
[22] Ram Murty, M. and Murty, K. V., Non-vanishing of L-functions and applications. Prog. Math., 157. Birkhäuser, Basel, 1997.Google Scholar
[23] Rotger, V. and Seveso, M. A., L-invariants and Darmon cycles attached to modular forms. http://sites.google.com/site/sevesomarco/publications. Google Scholar
[24] Seveso, M. A., Heegner cycles and derivatives of two variable p-adic L-functions. http://sites.google.com/site/sevesomarco/publications. Google Scholar
[25] Shimura, G., Introduction to the arithmetic theory of automorphic functions. Kanô Memorial Lectures, 1, Publications of the Mathematical Society of Japan, 11, Iwanami Shoten, Publishers, Tokyo; Princeton University Press, Princeton, N. J., 1971.Google Scholar
[26] Teitelbaum, J., Values of p-adic L-functions and a p-adic Poisson kernel. Invent. Math. 101(1990), no. 2, 395–410. http://dx.doi.org/10.1007/BF01231508Google Scholar