Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T05:38:05.501Z Has data issue: false hasContentIssue false
  • English
  • Français

Outer Partial Actions and Partial Skew Group Rings

Published online by Cambridge University Press:  20 November 2018

Patrik Nystedt  and
Johan Öinert
Patrik Nystedt
Affiliation:
University West, Department of Engineering Science, SE-46186 Trollhättan, Sweden. e-mail: [email protected]
Johan Öinert
Affiliation:
Centre for Mathematical Sciences, P.O. Box 118, Lund University, SE-22100 Lund, Sweden. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

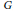We extend the classical notion of an outer action $\alpha $ of a group $G$ on a unital ring 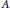$A$ to the case when $\alpha $ is a partial action on ideals, all of which have local units. We show that if $\alpha $ is an outer partial action of an abelian group 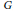$G$, then its associated partial skew group ring 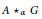$A\,{{\star }_{\alpha }}\,G$ is simple if and only if 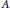$A$ is 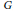$G$-simple. This result is applied to partial skew group rings associated with two different types of partial dynamical systems.

Keywords

16S3516W5037B0537B9954H1554H20outer actionpartial actionminimalitytopological dynamicspartial skew group ringsimplicity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 5 , 01 October 2015 , pp. 1144 - 1160
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Ánh, P. N. and Márki, L., Morita equivalence for rings without identity. Tsukuba J. Math. 11(1987),no. 1,1–16.Google Scholar
[2] Ávila, J. and Ferrero, M., Closed and prime ideals in partial skew group rings ofabelian groups. J. Algebra Appl. 10(2011), no. 5, 961–978.http://dx.doi.Org/10.1142/S0219498811005063 Google Scholar
[3] Beuter, V. and Gonçalves, D., Partial crossed products as equivalence relation algebras. Rocky Mountain J. Math., to appear. arxiv:1 306.3840Google Scholar
[4] Boava, G. and Exel, R., Partial crossed product description of the C*-algebras associated with integral domains. Proc. Amer. Math. Soc. 141(2013), no. 7, 2439–2451.http://dx.doi.Org/10.1090/S0002-9939-2013-11724-7 Google Scholar
[5] Crow, K., Simple regular skew group rings. J. Algebra Appl. 4(2005), no. 2,127–137.http://dx.doi.org/10.1142/S0219498805000909 Google Scholar
[6] Dokuchaev, M. and Exel, R., Associativity of crossed products by partial actions, enveloping actions and partial representations. Trans. Amer. Math. Soc. 357(2005), no. 5,1931–1952.http://dx.doi.Org/10.1090/S0002-9947-04-0351 9-6 Google Scholar
[7] Dokuchaev, M., Exel, R., and Simon, J. J., Crossed products by twisted partial actions and graded algebras. J. Algebra 320(2008), no. 8, 3278–3310.http://dx.doi.Org/10.1016/j.jalgebra.2008.06.023 Google Scholar
[8] Dokuchaev, M., Del Rio, A., and Simón, J. J., Globalizations of partial actions on nonunital rings. Proc. Amer. Math. Soc. 135(2007), no. 2, 343–352.http://dx.doi.Org/10.1090/S0002-9939-06-08503-0 Google Scholar
[9] Exel, R., Circle actions on C*-algebras, partial automorphisms, and a generalized Pimsner-Voiculescu exact sequence. J. Funct. Anal. 122(1994), no. 2, 361–401.http://dx.doi.Org/10.1006/jfan.1994.1073 Google Scholar
[10] Exel, R., The Bunce-Deddens algebras as crossed products by partial automorphisms. Bol. Soc. Brasil. Mat. (N.S.) 25(1994), no. 2,173–179.http://dx.doi.Org/10.1007/BF01321306 Google Scholar
[11] Exel, R., Approximately finite C*-algebras and partial automorphisms. Math. Scand. 77(1995),no. 2, 281–288.Google Scholar
[12] Exel, R., Partial actions of groups and actions of inverse semigroups. Proc. Amer. Math. Soc. 126(1998), no. 12, 3481–3494.http://dx.doi.Org/10.1090/S0002-9939-98-04575-4 Google Scholar
[13] Exel, R., Giordano, T., and Goncalves, D., Enveloping algebras of partial actions as groupoid C*-algebras. J. Operator Theory 65(2011), no. 1, 197–210.Google Scholar
[14] Exel, R. and Laca, M., Cuntz-Krieger algebras for infinite matrices. J. Reine Angew. Math. 512(1999), 119–172. http://dx.doi.Org/10.1515/crll.1999.051Google Scholar
[15] Fisher, J. W. and Montgomery, S., Semiprime skew group rings. J. Algebra 52(1978), no. 1, 241–247.http://dx.doi.Org/10.1016/0021-8693(78)90272-7 Google Scholar
[16] Gonçalves, D., Simplicity of partial skew group rings of abelian groups. Canad. Math. Bull. 57(2014), no. 3, 511–519. http://dx.doi.Org/10.4153/CMB-2014-011-1Google Scholar
[17] Gonçalves, D., Öinert, J., and Royer, D., Simplicity of partial skew group rings with applications to Leavittpath algebras and topological dynamics. J. Algebra 420(2014), 201–216.http://dx.doi.Org/10.1016/j.jalgebra.2O14.07.027 Google Scholar
[18] Haefner, J. and del Rio, A., The globalization problem for inner automorphisms and Skolem-Noether theorems. In: Algebras, rings and their representations, World Sci. Publ., Hackensack, NJ, 2006, pp. 37–51. http://dx.doi.Org/10.1142/9789812774552.0005 Google Scholar
[19] Lam, T. Y., A first course in noncommutative rings. Springer-Verlag, New York, 1991.http://dx.doi.Org/10.1007/978-1-4684-0406-7 Google Scholar
[20] McClanahan, K., K-theory for partial crossed products by discrete groups. J. Funct. Anal. 130(1995),no. 1, 77–117.http://dx.doi.Org/10.1006/jfan.1995.1064 Google Scholar
[21] Nystedt, P. and Öinert, J., Simple semigroup graded rings. J. Algebra Appl., to appear.http://dx.doi.Org/10.1142/S0219498815501029 Google Scholar
[22] Öinert, J., Simplicity of skew group rings ofabelian groups. Comm. Algebra 42(2014), no. 2,831–841.http://dx.doi.org/10.1080/00927872.2012.727052 Google Scholar