Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Horng-Jaan
and
Yeh, Cheh-Chih
1998.
Oscillation of nonlinear functional differential equations of the second order.
Applied Mathematics Letters,
Vol. 11,
Issue. 1,
p.
71.
Pei-guang, Wang
and
Wei-gao, GE
2000.
Forced oscillation of second-order neutral equations.
Applied Mathematics and Mechanics,
Vol. 21,
Issue. 10,
p.
1197.
Yang, Qigui
Yang, Lijun
and
Zhu, Siming
2003.
Interval criteria for oscillation of second-order nonlinear neutral differential equations.
Computers & Mathematics with Applications,
Vol. 46,
Issue. 5-6,
p.
903.
Jiang, Jianchu
and
Li, Xiaoping
2003.
Oscillation of second order nonlinear neutral differential equations.
Applied Mathematics and Computation,
Vol. 135,
Issue. 2-3,
p.
531.
Shi, Wenying
and
Wang, Peiguang
2003.
Oscillatory criteria of a class of second-order neutral functional differential equations.
Applied Mathematics and Computation,
Vol. 146,
Issue. 1,
p.
211.
Jiang, Jianchu
2003.
Oscillation of second order nonlinear neutral delay difference equations.
Applied Mathematics and Computation,
Vol. 146,
Issue. 2-3,
p.
791.
Şahiner, Y.
2004.
On oscillation of second order neutral type delay differential equations.
Applied Mathematics and Computation,
Vol. 150,
Issue. 3,
p.
697.
Xu, Run
and
Meng, Fanwei
2007.
Oscillation criteria for second order quasi-linear neutral delay differential equations.
Applied Mathematics and Computation,
Vol. 192,
Issue. 1,
p.
216.
Xu, Zhiting
and
Liu, Xiuxiang
2007.
Philos-type oscillation criteria for Emden–Fowler neutral delay differential equations.
Journal of Computational and Applied Mathematics,
Vol. 206,
Issue. 2,
p.
1116.
Xu, Zhiting
2007.
On the Oscillation of Second Order Neutral Differential Equations of Emden-Fowler Type.
Monatshefte für Mathematik,
Vol. 150,
Issue. 2,
p.
157.
Xu, Run
and
Meng, Fanwei
2007.
New Kamenev-type oscillation criteria for second order neutral nonlinear differential equations.
Applied Mathematics and Computation,
Vol. 188,
Issue. 2,
p.
1364.
Xu, Zhiting
2008.
Oscillation Theorems Related to Averaging Technique for Second Order Emden-Fowler Type Neutral Differential Equations.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 2,
Saker, Samir H.
O’regan, Donal
and
Agarwal, Ravi P.
2008.
Oscillation theorems for second-order nonlinear neutral delay dynamic equations on time scales.
Acta Mathematica Sinica, English Series,
Vol. 24,
Issue. 9,
p.
1409.
Hasanbulli, Mustafa
and
Rogovchenko, Yuri V.
2010.
Oscillation criteria for second order nonlinear neutral differential equations.
Applied Mathematics and Computation,
Vol. 215,
Issue. 12,
p.
4392.
Shi, Yanxiang
2014.
Oscillation criteria for nth order nonlinear neutral differential equations.
Applied Mathematics and Computation,
Vol. 235,
Issue. ,
p.
423.


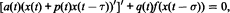
 . These results generalize and improve some known results about both neutral and delay differential equations.
. These results generalize and improve some known results about both neutral and delay differential equations.