Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-03T00:44:14.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation and Comparison Theorems for Second Order Linear Differential Equations with Integrable Coefficients

Published online by Cambridge University Press:  20 November 2018

G. Butler  and
J. W. Macki
G. Butler
Affiliation:
University of Alberta, Edmonton, Alberta
J. W. Macki
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical comparison and interlacing theorems of Sturm were originally proved for the equations

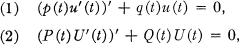
under the assumption that all coefficients are real-valued, continuous, and p > 0, P > 0. Atkinson [1, Chapter 8] has carried out the standard theory for eigenvalue problems involving (1), under the more general hypothesis

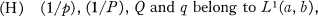
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 2 , April 1974 , pp. 294 - 301
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Atkinson, F. V., Discrete and continuous boundary problems (Academic Press, New York, 1964).Google Scholar
2. Cafiero, F., Su un problema ai limiti relativo alVequazione y′ = f(x, y,), Giorn. Mat. Battaglini 77 (1947), 145–163.Google Scholar
3. Diaz, J. B. and McLaughlin, J. R., Sturm separation and comparison theorems for ordinary and partial differential equations, Atti Accad. Naz. Lincei Mem. Cl. Sci. Fis. Mat. Natur. Sez. I, Series VIII, IX (1969), No. 5, 136–194.Google Scholar
4. Hartman, P., Ordinary differential equations (Wiley, New York, 1964).Google Scholar
5. Jakubovic, V. A., Oscillatory properties of the solutions of canonical equations, Mat. Sb. 56 (1962), 3–42; Amer. Math. Soc. Transi. 42 (1964), 247–288.Google Scholar
6. Kiasnosel'skii, M. A., Percov, A. I., Provolockii, A. I., and Zabreiko, P. P., Plane vector fields (Academic Press, New York, 1966).Google Scholar
7. Muldowney, J. S., On an inequality of Peano, Can. Math. Bull. 16 (1973), 79–82.Google Scholar
8. Reid, W. T., Some remarks on special disconjugacy criteria for differential systems, Pacific J. Math. 35 (1970), 763–772.Google Scholar
9. Reid, W. T., Generalized linear differential systems, J. Math. Mech. 8 (1959), 705–726.Google Scholar
10. Reid, W. T., Ordinary differential equations (Wiley, New York, 1971).Google Scholar