Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T04:36:59.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthogonal Matrices in Four-Space

Published online by Cambridge University Press:  20 November 2018

C. C. MacDuffee
C. C. MacDuffee*
Affiliation:
The University of Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every proper orthogonal matrix A can be written

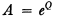
where Q is a skew matrix [6], and conversely every such matrix A is orthogonal. It is also known that every proper orthogonal transformation in real Euclidean four-space may be characterized in term of quaternions [1, 3] by the equation

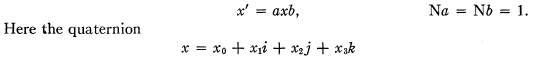
determines with the origin a vector having the coordinates (XQ, XI, x2, x3). The relationship between these two representations was clearly shown by Murnaghan [5].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 1 , Issue 1 , 01 February 1949 , pp. 69 - 72
Copyright
Copyright © Canadian Mathematical Society 1949

References

[1] Coxeter, H. S. M., American Mathematical Monthly, vol. 53 (1946), 136–146.Google Scholar
[2] Coxeter, H. S. M., Non-Euclidean Geometry (Toronto, 1942), 151–153.Google Scholar
[3] Guth, E., Anzeiger, Akademie der Wissenschaften in Wien, Mathematisch-naturwissenschaftliche Klasse, July 6, 1933, Nr. 18.Google Scholar
[4] MacDuffee, C. C., Monatshefte fur Mathematik und Physik, vol. 48 (1939), 294.Google Scholar
[5] Murnaghan, F. D., Scripta Mathematicat vol. 10 (1944), 37–49.Google Scholar
[6] Wedderburn, J. H. M., Ann. of Math., vol. 23 (1921), 134.Google Scholar