Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:49:30.659Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ordered K-theory of a Full Extension

Published online by Cambridge University Press:  20 November 2018

Søren Eilers ,
Gunnar Restorff  and
Efren Ruiz
Søren Eilers
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark. e-mail: [email protected]
Gunnar Restorff
Affiliation:
Faculty of Science and Technology, University of Faroe Islands, Nóatún 3, FO-100 Tórshavn, Faroe Islands. e-mail: [email protected]
Efren Ruiz
Affiliation:
Department of Mathematics, University of Hawaii, Hilo, 200 W. Kawili St., Hilo, Hawaii, 96720-4091, USA. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 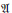$\mathfrak{A}$ be a 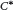${{C}^{*}}$-algebra with real rank zero that has the stable weak cancellation property. Let 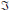$\Im $ be an ideal of 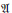$\mathfrak{A}$ such that 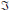$\Im $ is stable and satisfies the corona factorization property. We prove that

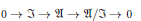$$0\,\to \,\Im \,\to \mathfrak{A}\,\to \,\mathfrak{A}/\Im \,\to \,0$$

is a full extension if and only if the extension is stenotic and $K$-lexicographic. As an immediate application, we extend the classification result for graph 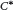${{C}^{*}}$-algebras obtained by Tomforde and the first named author to the general non-unital case. In combination with recent results by Katsura, Tomforde, West, and the first named author, our result may also be used to give a purely $K$-theoretical description of when an essential extension of two simple and stable graph 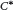${{C}^{*}}$-algebras is again a graph 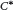${{C}^{*}}$- algebra.

Keywords

46L8046L3546L05classificationextensionsgraph algebras
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 3 , 01 June 2014 , pp. 596 - 624
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Ara, P., Goodearl, K. R., O’Meara, K. C., and Pardo, E., Separative cancellation for projective modules over exchange rings. Israel J. Math. 105(1998), 105–137. http://dx.doi.org/10.1007/BF02780325 Google Scholar
[2] Ara, P., Moreno, M. A., and Pardo, E., Nonstable K-theory for graph algebras. Algebr. Represent. Theory 10(2007), no. 2, 157–178. http://dx.doi.org/10.1007/s10468-006-9044-z Google Scholar
[3] Blackadar, B., K-theory for operator algebras. Second ed., Mathematical Sciences Research Institute Publications, 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[4] Brown, L. G., Semicontinuity and multipliers of C*-algebras. Canad. J. Math. 40(1988), no. 4, 865–988. http://dx.doi.org/10.4153/CJM-1988-038-5 Google Scholar
[5] Brown, L. G., Douglas, R. G., and Fillmore, P. A., Extensions of C*-algebras, operators with compact self-commutators, and K-homology. Bull. Amer. Math. Soc. 79(1973), 973–978. http://dx.doi.org/10.1090/S0002-9904-1973-13284-7 Google Scholar
[6] Brown, L. G., Unitary equivalence modulo the compact operators and extensions of C*-algebras. In: Proceedings of a Conference on Operator Theory (Dalhousie Univ., Halifax, N.S., 1973), Lecture Notes in Math., 345, Springer, Berlin, 1973, pp. 58–128.Google Scholar
[7] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99(1991), 131–149. http://dx.doi.org/10.1016/0022-1236(91)90056-B Google Scholar
[8] Carlsen, T. M., Eilers, S., and Tomforde, M., Index maps in the K-theory of graph algebras. J. K-theory, 9(2012), 385–406. http://dx.doi.org/10.1017/is011004017jkt156 Google Scholar
[9] Cuntz, J., K-theory for certain C*-algebras. Ann. of Math. (2) 113(1981), no. 1, 181–197. http://dx.doi.org/10.2307/1971137 Google Scholar
[10] Eilers, S., Katsura, T., Tomforde, M., and West, J., The ranges of K-theoretic invariants for nonsimple graph algebras. arxiv:1202.1989v1.Google Scholar
[11] Eilers, S., Loring, T. A., and Pedersen, G. K., Morphisms of extensions of C*-algebras: pushing forward the Busby invariant. Adv. Math. 147(1999), no. 1, 74–109. http://dx.doi.org/10.1006/aima.1999.1834 Google Scholar
[12] Eilers, S. and Restorff, G., On Rørdam's classification of certain C*-algebras with one non-trivial ideal. In: Operator Algebras: The Abel Symposium 2004, Abel Symp., 1, Springer, Berlin, 2006, pp. 87–96.Google Scholar
[13] Eilers, S., Restorff, G., and Ruiz, E., Classifying C*-algebras with both finite and infinite subquotients. J. Funct. Anal. 265(2013), no. 3, 449–468. http://dx.doi.org/10.1016/j.jfa.2013.05.006 Google Scholar
[14] Eilers, S., Classification of extensions of classifiable C*-algebras. Adv. Math. 222(2009), no. 6, 2153–2172. http://dx.doi.org/10.1016/j.aim.2009.07.014 Google Scholar
[15] Eilers, S., Strong classification of extension of classifiable C*-algebras. arxiv:1301.7695Google Scholar
[16] Eilers, S., On graph C*-algebras with a linear ideal lattice. Bull. Malays. Math. Sci. Soc. (2) 33(2010), no. 2, 233–241.Google Scholar
[17] Eilers, S. and Tomforde, M., On the classification of nonsimple graph C*-algebras. Math. Ann. 346(2010), no. 2, 393–418. http://dx.doi.org/10.1007/s00208-009-0403-z Google Scholar
[18] Elliott, G. A., On the classification of inductive limits of sequences of semisimple finite-dimensional algebras. J. Algebra 38(1976), no. 1, 29–44. http://dx.doi.org/10.1016/0021-8693(76)90242-8 Google Scholar
[19] Elliott, G. A. and Kucerovsky, D., An abstract Voiculescu-Brown-Douglas-Fillmore absorption theorem. Pacific J. Math. 198(2001), no. 2, 385–409. http://dx.doi.org/10.2140/pjm.2001.198.385 Google Scholar
[20] Goodearl, K. R. and Handelman, D. E., Stenosis in dimension groups and AF C*-algebras. J. Reine Angew. Math. 332(1982), 1–98.Google Scholar
[21] Handelman, D., Extensions for AF C*-algebras and dimension groups. Trans. Amer. Math. Soc. 271(1982), no. 2, 537–573.Google Scholar
[22] Hjelmborg, J. v. B. and Rørdam, M., On stability of C*-algebras. J. Funct. Anal. 155(1998), no. 1, 153–170. http://dx.doi.org/10.1006/jfan.1997.3221 Google Scholar
[23] Kirchberg, E. and Phillips, N. C., Embedding of exact C*-algebras in the Cuntz algebra O2. J. Reine Angew. Math. 525(2000), 17–53.Google Scholar
[24] Kucerovsky, D. and Ng, P.W., The corona factorization property and approximate unitary equivalence. Houston J. Math. 32(2006), no. 2, 531–550.Google Scholar
[25] Lin, H., Full extensions and approximate unitary equivalence. Pacific J. Math. 229(2007), no. 2, 389–428. http://dx.doi.org/10.2140/pjm.2007.229.389 Google Scholar
[26] Lin, H., C*-algebra extensions of C(X). Mem. Amer. Math. Soc. 115(1995), no. 550.Google Scholar
[27] Lin, H., Extensions by C*-algebras of real rank zero. II. Proc. London Math. Soc. (3) 71(1995), no. 3, 641–674. http://dx.doi.org/10.1112/plms/s3-71.3.641 Google Scholar
[28] Lin, H., Simple C*-algebras with continuous scales and simple corona algebras. Proc. Amer. Math. Soc. 112(1991), no. 3, 871–880.Google Scholar
[29] Lin, H., Ideals of multiplier algebras of simple AF C*-algebras. Proc. Amer. Math. Soc. 104(1988), no. 1, 239–244.Google Scholar
[30] Ng, P.W., The corona factorization property. In: Operator theory, operator algebras, and applications, Contemp. Math., 414, American Mathematical Society, Providence, RI, 2006, pp. 97–110.Google Scholar
[31] Pimsner, M., Popa, S., and Voiculescu, D., Homogeneous C*-extensions of C(X) ⊗ K(H). I. J. Operator Theory 1(1979), no. 1, pp. 55–108.Google Scholar
[32] Pimsner, M., Homogeneous C*-extensions of C(X) ⊗ K(H). II. J. Operator Theory, 4(1980), no. 2, 211–249.Google Scholar
[33] Rørdam, M., Ideals in the multiplier algebra of a stable C*-algebra. J. Operator Theory 25(1991), no. 2, 283–298.Google Scholar
[34] Rørdam, M., Classification of extensions of certain C*-algebras by their six term exact sequences in K-theory. Math. Ann. 308(1997), no. 1, 93–117. http://dx.doi.org/10.1007/s002080050067 Google Scholar
[35] Zhang, S., On the structure of projections and ideals of corona algebras. Canad. J. Math. 41(1989), no. 4, 721–742. http://dx.doi.org/10.4153/CJM-1989-033-4 Google Scholar
[36] Zhang, S., A property of purely infinite simple C*-algebras. Proc. Amer. Math. Soc. 109(1990), no. 3, 717–720.Google Scholar