Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-03T20:26:20.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Operators on the Fourier Algebra with Weakly Compact Extensions

Published online by Cambridge University Press:  20 November 2018

Charles F. Dunkl  and
Donald E. Ramirez
Charles F. Dunkl
Affiliation:
University of Virginia, Charlottesville, Virginia
Donald E. Ramirez
Affiliation:
University of Virginia, Charlottesville, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We let G denote an infinite compact group, and Ĝ its dual. We use the notation of our book [3, Chapters 7 and 8]. Recall that A(G) denotes the Fourier algebra of G (an algebra of continuous functions on G), and 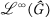denotes its dual space under the pairing 〈f, ϕ〉 , (f ∊ A (G), ϕ ∊ 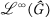). Further, note 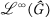is identified with the C*-algebra of bounded operators on L2(G) commuting with left translation. The module action of A (G) on 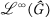is defined by the following: for f ∊ A (G), ϕ ∊ 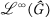, f · ϕ ∊ 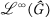by

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 2 , April 1974 , pp. 450 - 454
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Arens, R., The adjoint of a bilinear operation, Proc. Amer. Math. Soc. 2 (1951), 839–848.Google Scholar
2. Dunford, N. and Schwartz, J. T., Linear Operators. I: General theory , Pure and Appl. Math., Vol. 7 (Interscience, New York and London, 1958).Google Scholar
3. Dunkl, C. and Ramirez, D., Topics in harmonic analysis (Appleton, New York, 1971).Google Scholar
4. Dunkl, C. and Ramirez, D., Weakly almost periodic Junctionals on the Fourier algebra, Trans. Amer. Math. Soc. 185 (1973), 501–514.Google Scholar
5. Kluvánek, I., A compactness property of Fourier-Stieltjes transforms, Mat. Casopis, Slove. Akad. Vied 20 (1970), 84–86.Google Scholar
6. Moore, C., Groups with finite dimensional irreducible representations, Trans. Amer. Math. Soc. 166 (1972), 401–410.Google Scholar