Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T05:48:27.340Z Has data issue: false hasContentIssue false
  • English
  • Français

On Uniqueness Sets for Expansions in Sequences of Functions Arising from Singular Generating Functions

Published online by Cambridge University Press:  20 November 2018

Jet Wimp
Jet Wimp*
Affiliation:
Drexel University, Philadelphia, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let {pn(z)}; be a sequence of functions analytic in a region D. A problem in analysis which has received much attention is the following: describe the sets Z ⊂ D for which

(1)

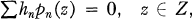
implies hn is 0 for all n, (To make the problem interesting, only those situations are studied where finite subsets of the pn(z) are linearly independent in D.) Another way of phrasing this is: Characterize the uniqueness sets of pn(z), a uniqueness set Z being a set in D such that the restriction of {pn(z)}; to Z is linearly independent. If Z is not a uniqueness set then for some {hn}; not all 0, we have

(2)

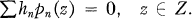
This formula is called a non-trivial representation of 0 (on Z).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 4 , 01 August 1981 , pp. 803 - 816
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Boas, R. P., Jr. and Buck, R. C., Polynomial expansions of analytic functions (Springer, Berlin, 1958).Google Scholar
2. Buckholtz, J. D., Appell polynomial expansions and bi-orthogonal expansions in Banach spaces, Trans. Amer. Math. Soc. 181 (1973), 245–272.Google Scholar
3. Buckholtz, J. D., Appell polynomials whose generating fmiction is meromorphic on its circle of convergence, Bull. Amer. Math. Soc. 79 (1973), 469–472.Google Scholar
4. Buckholtz, J. D., Series expansions of analytic functions, J. Math. Anal. Appl. 41 (1973), 673–684.Google Scholar
5. Buckholtz, J. D. and Shaw, J. K., Series expansions of analytic functions, II, Pacific J. Math. 56 (1975), 373–384.Google Scholar
6. Colton, D. L., Applications of a class of singular partial differential equations to Gegenbauer series which converge to zero, SIAM. J. Math. Anal. 1 (1970), 90–95.Google Scholar
7. Duren, P. L., Theory of HP spaces (Academic Press, N.Y., 1970).Google Scholar
8. Erdélyi, A. et. al., Higher transcendental functions (McGraw-Hill, N.Y., 1953).Google Scholar
9. Levin, B. Jr., Distribution of zeros of entire functions, Amer. Math. Soc. (Providence, R.I., 1964), 219.Google Scholar
10. Read, G. A., Expansion in series of polynomials, J. London. Math. Soc. 43 (1968), 655–657.Google Scholar
11. Rudin, W., Lectures on the edge-of-the-wedge theorem, Amer. Math. Soc. Monograph 6 (Providence, R.I., 1971).Google Scholar
12. Wimp, J., Uniform scale functions and the asymptotic expansion of integrals, Proc. 1978 Dundee Conference on Differential Equations (Springer, Berlin, 1978).Google Scholar
13. Wimp, J. and Colton, D. L., Jacobi series which converge to zero, with applications to a class of singular partial differential equations, Proc. Cambridge Phil. Soc. 65 (1969), 101–106.Google Scholar
14. Wimp, J. and Colton, D. L., Remarks on the representation of zero by solutions of differential equations, Proc. A.M.S. 74 (1979), 232–234.Google Scholar
15. Wright, E. M., On the coefficients of power series having exponential singularities, II, J. Lon. Math. Soc. 24 (1949), 304–309.Google Scholar