Hostname: page-component-5cf477f64f-tx7qf Total loading time: 0 Render date: 2025-04-05T22:00:14.409Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Zariski-van Kampen Theorem

Published online by Cambridge University Press:  20 November 2018

Ichiro Shimada
Ichiro Shimada*
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060-0810, Japan, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 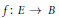$f:\,E\,\to \,B$ be a dominant morphism, where 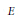$E$ and 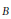$B$ are smooth irreducible complex quasi-projective varieties, and let 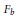${{F}_{b}}$ be the general fiber of $f$. We present conditions under which the homomorphism 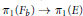${{\text{ }\!\!\pi\!\!\text{ }}_{1}}\left( {{F}_{b}} \right)\,\to \,{{\text{ }\!\!\pi\!\!\text{ }}_{1}}\,\left( E \right)$ induced by the inclusion is injective.

Keywords

14F35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 1 , 01 February 2003 , pp. 133 - 156
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Deligne, Pierre, Le groupe fondamental du complément d'une courbe plane n'ayant que des points doubles ordinaires est abélien (d'après W. Fulton). In: Bourbaki Seminar, Vol. 1979/80, Lecture Notes in Math. 842, Springer, Berlin, 1981, 1–10.Google Scholar
[2] Dimca, Alexandru, Singularities and topology of hypersurfaces. Springer-Verlag, New York, 1992.Google Scholar
[3] Fulton, William and Lazarsfeld, Robert, Connectivity and its applications in algebraic geometry. In: Algebraic geometry (Chicago, Ill., 1980), Lecture Notes in Math. 862, Springer, Berlin, 1981, 26–92.Google Scholar
[4] Matsuno, Takanori, On a theorem of Zariski-van Kampen type and its applications, Osaka J. Math. (3) 32 (1995), 645–658.Google Scholar
[5] Nori, Madhav V., Zariski's conjecture and related problems. Ann. Sci. E´ cole Norm. Sup. (4) 16 (1983), 305–344.Google Scholar
[6] Shimada, Ichiro, Fundamental groups of open algebraic varieties. Topology (3) 34 (1995), 509–531.Google Scholar
[7] Shimada, Ichiro, A generalization of Lefschetz-Zariski theorem on fundamental groups of algebraic varieties. Internat. J. Math. (6) 6 (1995), 921–932.Google Scholar
[8] Shimada, Ichiro, A note on Zariski pairs. Compositio Math. (2) 104 (1996), 125–133.Google Scholar
[9] Shimada, Ichiro, Fundamental groups of complements to singular plane curves. Amer. J. Math. (1) 119 (1997), 127–157.Google Scholar
[10] Shimada, Ichiro, On the commutativity of fundamental groups of complements to plane curves. Math. Proc. Cambridge Philos. Soc. (1) 123 (1998), 49–52.Google Scholar
[11] Shimada, Ichiro, Fundamental groups of algebraic fiber spaces. Comment.Math. Helv., to appear.Google Scholar
[12] Shimada, Ichiro, Zariski hyperplane section theorem for Grassmannian varieties. Canad. J. Math., 55 (2003), 157–180.Google Scholar
[13] van Kampen, E. R., On the fundamental group of algebraic curve. Amer. J. Math. 55 (1933), 255–260.Google Scholar
[14] Zariski, Oscar, On the problem of existence of algebraic functions of two variables possessing a given branch curve. Amer. J. Math. 51 (1929), 305–328; Collected Papers, Volume III. The MIT Press, Cambridge, Mass.-London, 1978, 123–146.Google Scholar