Article contents
On the Weak Order of Coxeter Groups
Published online by Cambridge University Press: 10 January 2019
Abstract
This paper provides some evidence for conjectural relations between extensions of (right) weak order on Coxeter groups, closure operators on root systems, and Bruhat order. The conjecture focused upon here refines an earlier question as to whether the set of initial sections of reflection orders, ordered by inclusion, forms a complete lattice. Meet and join in weak order are described in terms of a suitable closure operator. Galois connections are defined from the power set of 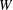 $W$ to itself, under which maximal subgroups of certain groupoids correspond to certain complete meet subsemilattices of weak order. An analogue of weak order for standard parabolic subsets of any rank of the root system is defined, reducing to the usual weak order in rank zero, and having some analogous properties in rank one (and conjecturally in general).
$W$ to itself, under which maximal subgroups of certain groupoids correspond to certain complete meet subsemilattices of weak order. An analogue of weak order for standard parabolic subsets of any rank of the root system is defined, reducing to the usual weak order in rank zero, and having some analogous properties in rank one (and conjecturally in general).
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
- 11
- Cited by


