Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T23:26:39.581Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Vector Sum of Two Convex Sets in Space

Published online by Cambridge University Press:  20 November 2018

Steven G. Krantz  and
Harold R. Parks
Steven G. Krantz
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences 1364 Budapest, P. O. Box 12 Hungary.
Harold R. Parks
Affiliation:
Department of Mathematics and Statistics McMaster University, HamiltonOntario L8S4K1.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

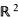In the paper [KIS2], C. Kiselman studied the boundary smoothness of the vector sum of two smoothly bounded convex sets A and B in . He discovered the startling fact that even when A and B have real analytic boundary the set A + B need not have boundary smoothness exceeding C20/3 (this result is sharp). When A and B have C∞ boundaries, then the smoothness of the sum set breaks down at the level C5 (see [KIS2] for the various pathologies that arise).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 2 , 01 April 1991 , pp. 347 - 355
Copyright
Copyright © Canadian Mathematical Society 1991

References

[ALA] Allard, W. and Almgren, F.J., An introduction to regularity theory for parametric elliptic variational problems, Proc. Symp. Pure Math. XXIII, 1971.Google Scholar
[AD] Anderson, W.N. and Duffln, R.J., Series and parallel addition of matrices, J. Math. Analysis Appl. 26(1969), 576–594.Google Scholar
[BAR] Baouendi, M.S. and Rothschild, L.P., Germs of CR maps between real analytic hypersurfaces, Invent. Math. 93(1988), 481–500.Google Scholar
[BOM] Boman, J., Smoothness of sums of convex sets with real analytic boundaries, Math. Scand., to appear.Google Scholar
[JPD] D'Angelo, J.P., The notion of formal essential finiteness for smooth real hypersurfaces, Indiana Univ. Math. Jour. 36(1987), 897–903.Google Scholar
[FED1] Fédérer, H., Geometric Measure Theory, Springer, New York and Berlin(1970).Google Scholar
[FED2] Fédérer, H., Curvature Measures, Trans. A. M. S. 93(1959), 418–491.Google Scholar
[FEK] Fefferman, C.L. and Kohn, J.J., Holder estimates on domains of complex dimension two and on three dimensional CR manifolds Advances in Math. 69(1988), 223–303.Google Scholar
[FOK] Folland, G.B. and Kohn, J.J., The Neumann Problem for the Cauchy-Riemann Complex, Princeton University Press, Princeton, 1972.Google Scholar
[KIS1] Kiselman, C.O., How smooth is the shadow of smooth convex body?, J. London Math. Soc. 33(1986), 101–109.Google Scholar
[KIS2] Kiselman, C.O., Smoothness of vector sums of plane convex sets, Math. Scand. 60(1987), 239–252.Google Scholar
[KRP] Krantz, S.G. and Parks, H.R., Distance to Ck hypersurfaces, Jour. Diff. Equations 40(1981), 116–120.Google Scholar
[PEN] Penrose, R., A generalized inverse for matrices, Proc. Cambridge Phil. Soc. 51(1955), 406–413.Google Scholar