Article contents
On the Uniform Approximation of Smooth Functions by Jacobi Polynomials
Published online by Cambridge University Press: 20 November 2018
Extract
Let ωn(x) denote the Jacobi polynomials with the weight Function

If we denote the corresponding normalized Jacobi polynomials by 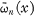 we Have
we Have
(1.1)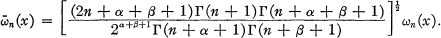
Now let
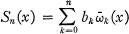
be the nth partial sum of the Fourier series of Jacobi polynomials of a function f(x).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1973
References
- 1
- Cited by


