Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T03:19:02.543Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Structure of Certain Nest Algebra Modules

Published online by Cambridge University Press:  20 November 2018

G. J. Knowles
G. J. Knowles*
Affiliation:
Texas Tech University, Lubbock, Texas
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 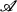be a nest algebra of operators on some Hilbert space H. Weakly closed 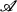-modules were first studied by J. Erdos and S. Power in [4]. It became apparent that many interesting classes of non self-adjoint operator algebras arise as just such a module. This paper undertakes a systematic investigation of the correspondence which arises between such modules and order homomorphisms from Lat 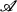into itself. This perspective provides a basis to answer some open questions arising from [4]. In particular, the questions concerning unique “determination” and characterization of maximal and minimal elements under this correspondence, are resolved. This is then used to establish when the determining homomorphism is unique.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 6 , 01 December 1987 , pp. 1405 - 1412
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Knowles, G. J., Dissertation, Kings College (University of London, 1981).Google Scholar
2. Knowles, G. J., Nest algebra-modules; commutants and cohomology, (Submitted).Google Scholar
3. Erdos, J. A., Operators of finite rank in nest algebras, J. London Math. Soc. 43 (1968), 391–397.Google Scholar
4. Erdos, J. A. and Power, S. C., Weakly closed ideals of nest algebras, J. Op. Theory 7 (1982), 219–235.Google Scholar
5. Ringrose, J. R., On some algebras of operators, Proc. London Math. Soc. (3) 15 (1965), 61–83.Google Scholar