Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-04T18:14:50.768Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Smallest Degrees of Projective Representations of the Groups PSL(n, q)

Published online by Cambridge University Press:  20 November 2018

Morton E. Harris  and
Christoph Hering
Morton E. Harris
Affiliation:
University of Illinois at Chicago Circle, Chicago, Illinois
Christoph Hering
Affiliation:
University of Illinois at Chicago Circle, Chicago, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we obtain information about the minimal degree δ of any non-trivial projective representation of the group PSL(n, q) with n ≧ 2 over an arbitrary given field K. Our main results for the groups PSL(n, q) (Theorems 4.2, 4.3, and 4.4) state that, apart from certain exceptional cases with small n, we have the following rather surprising situation: if q = pf (where p is a prime integer) and char K = p, then δ = n, but if q = pf and char K ≠ p, then δ is of a considerably higher order of magnitude, namely, δ is at least qn–l – 1 or 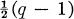if n = 2 and q is odd. Note that for n = 2, this lower bound for δ is the best possible. However, for n ≧ 3, this lower bound can conceivably be improved.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 1 , February 1971 , pp. 90 - 102
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Brauer, R., Zur Darstellungstheorie der Gruppen endlicher Ordnung, Math. Z. 63 (1956), 406–444.Google Scholar
2. Cartan, H. and Eilenberg, S., Homologuai algebra (Princeton Univ. Press, Princeton, N.J., 1956).Google Scholar
3. Gorenstein, D., Finite groups (Harper and Row, New York, 1968).Google Scholar
4. Higman, D. G., Flag-transitive collineation groups of finite projective spaces, Illinois J. Math. 6 (1962), 434–446.Google Scholar
5. Hering, C., On transitive linear groups (in preparation).Google Scholar
6. Huppert, B., Endliche Gruppen. I (Springer-Verlag, Berlin, 1967).Google Scholar
7. MacLane, S., Homology (Springer-Verlag, Berlin, 1963).Google Scholar
8. Rim, D. S., Modules over finite groups, Ann. of Math. (2) 69 (1959), 700–712.Google Scholar