No CrossRef data available.
Article contents
On the roots of polynomials with log-convex coefficients
Published online by Cambridge University Press: 15 February 2022
Abstract
In this paper, we consider the family of nth degree polynomials whose coefficients form a log-convex sequence (up to binomial weights), and investigate their roots. We study, among others, the structure of the set of roots of such polynomials, showing that it is a closed convex cone in the upper half-plane, which covers its interior when n tends to infinity, and giving its precise description for every
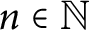 $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
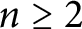 $n\geq 2$
. Dual Steiner polynomials of star bodies are a particular case of them, and so we derive, as a consequence, further properties for their roots.
$n\geq 2$
. Dual Steiner polynomials of star bodies are a particular case of them, and so we derive, as a consequence, further properties for their roots.
Keywords
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society, 2022
Footnotes
This research is part of the project PGC2018-097046-B-I00, supported by MCIN/AEI/10.13039/501100011033/FEDER “Una manera de hacer Europa.” It is also supported by Fundación Séneca, project 19901/GERM/15.



