No CrossRef data available.
Article contents
On the Restricted Cesàro Summability of Multiple Orthogonal Series
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We actually treat double orthogonal series in detail, simply for the sake of brevity in notations. Multiple orthogonal series will be shortly indicated in the concluding Section 8.
Let (X, 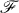 , μ) be an arbitrary positive measure space and {ϕjk(x):i, k = 0, 1, …} an orthonormal system defined on X. We consider the double orthogonal series
, μ) be an arbitrary positive measure space and {ϕjk(x):i, k = 0, 1, …} an orthonormal system defined on X. We consider the double orthogonal series
(1.1)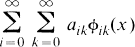
where {ϕik:i, k = 0, 1, …} is a double sequence of real numbers (coefficients), for which
(1.2)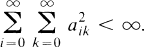
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1985
References
1.
Alexits, G., Convergence problems of orthogonal series (Pergamon Press, Oxford-New York, 1961).Google Scholar
2.
Móricz, F., On the restricted convergence and (C, 1, 1)-summability of double orthogonal series, Acta Sci. Math. (Szeged) (to appear).Google Scholar
3.
Móricz, F., On the (C, α ≧ 0, β ≧ 0)-summability of double orthogonal series, Studia Math, (to appear).CrossRefGoogle Scholar
4.
Zygmund, A., Sur l'application de la première moyenne arithmétique dans la théorie des séries de fonctions orthogonales, Fund. Math.
10 (1927), 356–362.Google Scholar


