Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T06:48:09.763Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Pointwise Bishop–Phelps–Bollobás Property for Operators

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  17 October 2018

Sheldon Dantas Open the ORCID record for Sheldon Dantas [Opens in a new window] ,
Vladimir Kadets ,
Sun Kwang Kim ,
Han Ju Lee  and
Miguel Martín
Sheldon Dantas
Affiliation:
Department of Mathematics, Faculty of Electrical Engineering, Czech Technical University in Prague, Technická 2, 166 27 Prague 6, Czech Republic Email: [email protected]
Vladimir Kadets
Affiliation:
School of Mathematics and Computer Sciences, V. N. Karazin Kharkiv National University, pl. Svobody 4, 61022 Kharkiv, Ukraine Email: [email protected]
Sun Kwang Kim
Affiliation:
Department of Mathematics, Chungbuk National University, 1 Chungdae-ro, Seowon-Gu, Cheongju, Chungbuk 28644, Republic of Korea Email: [email protected]
Han Ju Lee
Affiliation:
Department of Mathematics Education, Dongguk University - Seoul, 04620 (Seoul), Republic of Korea Email: [email protected]
Miguel Martín
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study approximation of operators between Banach spaces 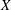$X$ and 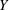$Y$ that nearly attain their norms in a given point by operators that attain their norms at the same point. When such approximations exist, we say that the pair 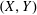$(X,Y)$ has the pointwise Bishop–Phelps–Bollobás property (pointwise BPB property for short). In this paper we mostly concentrate on those 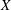$X$, called universal pointwise BPB domain spaces, such that 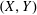$(X,Y)$ possesses pointwise BPB property for every 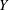$Y$, and on those 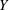$Y$, called universal pointwise BPB range spaces, such that 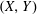$(X,Y)$ enjoys pointwise BPB property for every uniformly smooth 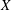$X$. We show that every universal pointwise BPB domain space is uniformly convex and that 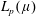$L_{p}(\unicode[STIX]{x1D707})$ spaces fail to have this property when 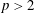$p>2$. No universal pointwise BPB range space can be simultaneously uniformly convex and uniformly smooth unless its dimension is one. We also discuss a version of the pointwise BPB property for compact operators.

Keywords

Banach spacenorm-attaining operatorBishop–Phelps–Bollobás property

MSC classification

Primary: 46B04: Isometric theory of Banach spaces
Secondary: 46B07: Local theory of Banach spaces 46B20: Geometry and structure of normed linear spaces
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 6 , December 2019 , pp. 1421 - 1443
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The corresponding author is H. J. Lee. The research of the first author was supported by the Centrum pokročilých aplikovaných přírodních věd (Center for Advanced Applied Science) project OPVVV CAAS CZ.02.1.01/0.0/0.0/16_019/0000778, by Pohang Mathematics Institute (PMI), POSTECH, Korea, and by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science, and Technology (NRF-2015R1D1A1A09059788). The research of the second author was done with the support of the Ukrainian Ministry of Science and Education Research Program 0118U002036, and was partially supported by Spanish MINECO/FEDER projects MTM2015-65020-P and MTM2017-83262-C2-2-P. The third author was partially supported by the Basic Science Research Program through the National Research Foundation of Korea(NRF), funded by the Ministry of Education, Science and Technology (NRF-2017R1C1B1002928). The fourth author was partially supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science and Technology (NRF-2016R1D1A1B03934771). The fifth author was partially supported by Spanish MINECO/FEDER grant MTM2015-65020-P.

References

Acosta, M. D., The Bishop-Phelps-Bollobás property for operators on C(K) . Banach J. Math. Anal. 10(2016), 307–319. https://doi.org/10.1215/17358787-3492875 Google Scholar
Acosta, M. D., Aguirre, F. J., and Payá, R., A new sufficient condition for the denseness of norm attaining operators . Rocky Mountain J. Math. 26(1996), 407–418. https://doi.org/10.1215/17358787-3492875 Google Scholar
Acosta, M. D., Aron, R. M., García, D., and Maestre, M., The Bishop-Phelps-Bollobás theorem for operators . J. Funct. Anal. 294(2008), 2780–2899. https://doi.org/10.1016/j.jfa.2008.02.014 Google Scholar
Acosta, M. D., Becerra-Guerrero, J., Choi, Y. S., Ciesielski, M., Kim, S. K., Lee, H. J., Lourenço, M. L., and Martín, M., The Bishop-Phelps-Bollobás property for operators between spaces of continuous funtions . Nonlinear Anal. 95(2014), 323–332. https://doi.org/10.1016/j.na.2013.09.011 Google Scholar
Acosta, M. D., Becerra-Guerrero, J., García, D., and Maestre, M., The Bishop-Phelps-Bollobás Theorem for bilinear forms . Trans. Amer. Math. Soc. 365(2013), 5911–5932. https://doi.org/10.1090/S0002-9947-2013-05881-3 Google Scholar
Acosta, M. D., Mastyło, M., and Soleimani-Mourchehkhorti, M., The Bishop-Phelps-Bollobás and approximate hyperplane series properties . J. Funct. Anal. 274(2018), no. 9, 2673–2699. https://doi.org/10.1016/j.jfa.2017.09.008 Google Scholar
Aron, R. M., Cascales, B., and Kozhushkina, O., The Bishop-Phelps-Bollobás theorem and Asplund operators . Proc. Amer. Math. Soc. 139(2011), no. 10, 3553–3560. https://doi.org/10.1090/S0002-9939-2011-10755-X Google Scholar
Aron, R., Choi, Y. S., Kim, S. K., Lee, H. J., and Martín, M., The Bishop-Phelps-Bollobás version of Lindenstrauss properties A and B . Trans. Amer. Math. Soc. 367(2015), 6085–6101. https://doi.org/10.1090/S0002-9947-2015-06551-9 Google Scholar
Cascales, B., Guirao, A. J., Kadets, V., and Soloviova, M., 𝛤-Flatness and Bishop-Phelps-Bollobás type theorems for operators . J. Funct. Anal. 274(2018), no. 3, 863–888. https://doi.org/10.1016/j.jfa.2017.10.020 Google Scholar
Cho, D. H. and Choi, Y. S., The Bishop-Phelps-Bollobás theorem on bounded closed convex sets . J. Lond. Math. Soc. 93(2016), 502–518. https://doi.org/10.1112/jlms/jdw002 Google Scholar
Choi, Y. S., Dantas, S., Jung, M., and Martín, M., On the Bishop-Phelps-Bollobás property and absolute sums. ArXiv preprint (2018). https://arxiv.org/abs/1806.09366.Google Scholar
Dantas, S., García, D., Maestre, M., and Martín, M., The Bishop-Phelps-Bollobás property for compact operators . Canad. J. Math. 70(2018), no. 1, 53–73. https://doi.org/10.4153/CJM-2016-036-6 Google Scholar
Dantas, S., Kim, S. K., and Lee, H. J., The Bishop-Phelps-Bollobás point property . J. Math. Anal. Appl. 444(2016), 1739–1751. https://doi.org/10.1016/j.jmaa.2016.07.009 Google Scholar
Diestel, J., Geometry of Banach spaces—selected topics . Lecture Notes in Mathematics, 485, Springer-Verlag, Berlin, 1975.Google Scholar
Fabian, M., Habala, P., Hàjek, P., Santalucía, V. M., Pelant, J., and Zizler, V., Functional analysis and infinite-dimensional geometry . CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, 8, Springer-Verlag, New York, 2001. https://doi.org/10.1007/978-1-4757-3480-5 Google Scholar
Figiel, T., On the moduli of convexity and smoothness . Studia Math. 56(1976), 121–155. https://doi.org/10.4064/sm-56-2-121-155 Google Scholar
Gurariĭ, V. I., On moduli of convexity and flattening of Banach spaces . (English. Russian original) Sov. Math., Dokl. 6(1965), 535–539; translation from Dokl. Akad. Nauk SSSR 161(1965), 1003–1006.Google Scholar
Kadets, V., López, G., Martín, M., and Werner, D., Equivalent norms with an extremely nonlineable set of norm attaining functionals . J. Inst. Math. Jussieu, to appear. https://doi.org/10.1017/S1474748018000087 Google Scholar
Kim, S. K. and Lee, H. J., Uniform convexity and Bishop-Phelps-Bollobás property . Canad. J. Math. 66(2014), 373–386. https://doi.org/10.4153/CJM-2013-009-2 Google Scholar
Pisier, G., Martingales with values in uniformly convex spaces . Israel J. Math. 20(1975), 326–350. https://doi.org/10.1007/BF02760337 Google Scholar
Lazar, A. J. and Lindenstrauss, J., Banach spaces whose duals are L 1 spaces and their representing matrices . Acta Math. 126(1971), 165–193. https://doi.org/10.2307/1996220 Google Scholar
Nielsen, N. J. and Olsen, G. H., Complex preduals of L 1 and subspaces of ℓ ∞ n (ℂ) . Math. Scand. 40(1977), 271–287. https://doi.org/10.7146/math.scand.a-11694 Google Scholar