Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-12T05:24:36.389Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Associative Triples in an Algebra of n Elements

Published online by Cambridge University Press:  20 November 2018

P. J. Brockwell
P. J. Brockwell*
Affiliation:
Argonne National Laboratory, Argonne, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a set of n elements α1, … , αn (denoted by S) and the set of all possible multiplication tables on these elements. The total number of such tables is clearly 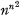and each table can be represented by a square matrix [μij] where μij is the product αiαj (μij ∈ S, i = 1, … , n; j = 1, … , n). The triple (αi, αj, αk) is said to be associative if the following equation is satisfied:

1.1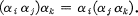

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 842 - 850
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Climescu, A. C., Etudes sur la théorie des systèmes multiplicatifs uniformes. I—L'indice de non-associativité, Bull. Ecole Polytech. Jassy, 2 (1947), 347–371.Google Scholar
2. Straus, E. G. and Wilf, H. S., Combinatorial aspects of the associative law of arithmetic (unpublished).Google Scholar