Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-18T18:54:38.840Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Invariant Factors of Class Groups in Towers of Number Fields

Published online by Cambridge University Press:  20 November 2018

Farshid Hajir  and
Christian Maire
Farshid Hajir
Affiliation:
Department of Mathematics & Statistics, University of Massachusetts, Amherst MA 01003, USA e-mail: [email protected]
Christian Maire
Affiliation:
Laboratoire de Mathématiques, Université Bourgogne Franche-Comté et CNRS, (UMR 6623), 16 route deGray, 25030 Besançon cédex, France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite abelian 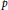$p$-group 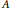$A$ of rank 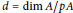$d\,=\,\dim\,A/pA$, let 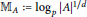${{\mathbb{M}}_{A}}\,:=\,\text{lo}{{\text{g}}_{p}}\,{{\left| A \right|}^{1/d}}$ be its (logarithmic) mean exponent. We study the behavior of the mean exponent of 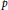$p$-class groups in pro-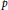$p$ towers 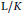$\text{L/K}$ of number fields. Via a combination of results from analytic and algebraic number theory, we construct infinite tamely ramified pro-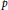$p$ towers in which the mean exponent of 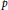$p$-class groups remains bounded. Several explicit examples are given with 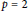$p\,=\,2$. 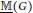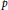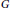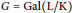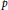Turning to group theory, we introduce an invariant $\underline{\mathbb{M}}\left( G \right)$ attached to a finitely generated pro-$p$ group $G$; when $G\,=\,\text{Gal}\left( \text{L/K} \right)$, where $L$ is the Hilbert $p$-class field tower of a number field 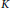$K$, 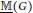$\underline{\mathbb{M}}\left( G \right)$ measures the asymptotic behavior of the mean exponent of 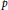$p$-class groups inside 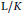$\text{L/K}$. We compare and contrast the behavior of this invariant in analytic versus non-analytic groups. We exploit the interplay of group-theoretical and number-theoretical perspectives on this invariant and explore some open questions that arise as a result, which may be of independent interest in group theory.

Keywords

11R2911R37class field towerideal class grouppro-p groupp-adic analytic groupBrauer-Siegel Theorem
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 1 , 01 February 2018 , pp. 142 - 172
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Brumer, A., Pseudocompact algebras, profinite groups and class formations. J. Algebra 4(1966), 442–470.http://dx.doi.Org/10.1016/0021-8693(66)90034-2 Google Scholar
[2] J. W. S.|Cassels and Fröhlich [eds], A., Algebraic number theory. Proceedings of the instructional conference held at the University of Sussex, Brighton, September 1-17,1965, Academic Press, New York, 1967.Google Scholar
[3] Coates, J., Schneider, P., and Sujatha, R., Modules over Iwasawa algebras. J. Inst. Math. Jussieu 2(2003), no. 1, 73–108.http://dx.doi.Org/10.1017/S1474748003000045 Google Scholar
[4] Dixon, J. D., du Sautoy, M. P. F., Mann, A., and Segal, D., Analytic pro-p-groups. Cambridge Studies in Advanced Mathematics, 61, Cambridge University Press, Cambridge, 1999.http://dx.doi.Org/10.1017/CBO9780511470882 Google Scholar
[5] Ershov, M., Golod-Shafarevich groups: a survey. Internat. J. Algebra Comput. 22(2012), no. 5, 1230001.http://dx.doi.Org/10.1142/S0218196712300010 Google Scholar
[6] Ershov, M., Kazhdan quotients of Golod-Shafarevich groups. Proc. Lond. Math. Soc. 102(2011), no. 4, 599–636.http://dx.doi.Org/10.1112/plms/pdq022 Google Scholar
[7] Fontaine, J.-M. and Mazur, B., Geometric Galois representations. In :Elliptic curves, modular forms, and Fermat's last theorem (Hong Kong, 1993), Ser. Number Theory, I, Int. Press, Cambridge, MA, 1995, pp. 41–78.Google Scholar
[8] Forré, P., Strongly free sequences and pro-p-groups of cohomological dimension 2. J. reine angew.Math. 658(2011), 173–192.http://dx.doi.Org/10.1515/CRELLE.2O11.067 Google Scholar
[9] Friedman, E., Analytic formulas for the regulator of a number field. Invent. Math. 98(1989), no. 3, 599–622.http://dx.doi.org/10.1007/BF01393839 Google Scholar
[10] Gartner, J., Mild pro-p-groups with trivial cup-product. PhD thesis, University of Heidelberg, 2011.Google Scholar
[11] Gartner, J., On p-class groups and the Fontaine-Mazur conjecture. Math. Res. Lett. 21(2014), 469–477.http://dx.doi.org/10.4310/MRL.2014.v21.n3.a5 Google Scholar
[12] Gras, G., Class field theory. Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.http://dx.doi.org/10.1007/978-3-662-11323-3 Google Scholar
[13] Gras, G. and Munnier, A., Extensions cycliques T-totalement ramifiées. Publ. Math. UFR Sci. Tech. Besançon, 1999.Google Scholar
[14] Hajir, F., On the growth of p-class groups in p-class field towers. J. Algebra 188(1997), no. 1, 256–271.http://dx.doi.Org/10.1006/jabr.1 996.6849 Google Scholar
[15] Hajir, F. and Maire, C., Tamely ramified towers and discriminant bounds for number fields. Compositio Math. 128(2001), no. 1, 35–53. http://dx.doi.Org/10.1023/A:101753741 5688 Google Scholar
[16] Hajir, F., Extensions of number fields with bounded ramification of bounded depth. Int. Math. Res. Not. 13(2002), 677–696.http://dx.doi.org/10.1155/S1073792 802106015 Google Scholar
[17] Harris, M., p-adic representations arising from descent on abelian varieties.Compositio Math. 39(1979), no. 2,177-245; with correction: Compositio Math. 121(2000), 105–108. http://dx.doi.Org/10.1023/A:100173061694 Google Scholar
[18] Ihara, Y., How many primes decompose completely in an infinite unramified Galois extension of a global field?. J. Math. Soc. Japan 35(1983), no. 4, 693–709.http://dx.doi.Org/10.2969/jmsj/03540693 Google Scholar
[19] Iwasawa, K., On the μ-invariants of -extensions. In: Number theory, algebraic geometry and commutative algebra, in honor of Yasuo Akizuki, Kinokuniya, Tokyo, 1973, pp. 1–11.Google Scholar
[20] Koch, H., Galoissche Theorie der p-Erweiterungen. Springer-Verlag, Berlin-New York, 1970.Google Scholar
[21] Labute, J., Mildpro-p-groups and Galois groups of p-extensions of . J. Reine Angew. Math. 596(2006), 155–182.http://dx.doi.org/10.1515/CRELLE.2006.058 Google Scholar
[22] Labute, J. and Minàč, J., Mildpro-2-groups and 2-extensions of with restricted ramification. J. Algebra 332(2011), 136–158.http://dx.doi.Org/10.1016/j.jalgebra.2011.01.019 Google Scholar
[23] Lang, S., Algebraic number theory. Second ed., Graduate Texts in Mathematics, 110, Springer-Verlag, New York, 1994.http://dx.doi.org/10.1007/978-1-4612-0853-2 Google Scholar
[24] Lazard, M., Groupes analytiques p-adiques. Inst. Hautes Études Sci. Publ. Math. 26(1965), 389–603.Google Scholar
[25] Maire, C., Finitude de tours et p-tours T-ramifiées modérées, S-décomposées. J. Théor. Nombres Bordeaux 8(1996), 47–73..http://dx.doi.org/10.1007/s00209-009-0652-2 Google Scholar
[26] Maire, C., T-S- capitulation. In: Théorie des nombres, Années 1994/95-1995/96, Publ. Math. Fac. Sci. Besançon, 1997.Google Scholar
[27] Maire, C., Sur la structure galoisienne de certaines pro-p-extensions de corps de nombres. Math. Z. 267(2011), no. 3-4, 887–913.http://dx.doi.org/10.1007/s00209-009-0652-2 Google Scholar
[28] Matsumura, H., Commutative ring theory. Cambridge Studies in Advanced Mathematics, 8, Cambridge University Press, Cambridge, 1989.Google Scholar
[29] McLeman, M., A Golod-Shafarevich equality and p-tower groups. J. Number Theory 129(2009), no. 11, 2808–2819.http://dx.doi.org/10.1016/j.jnt.2009.05.014 Google Scholar
[30] Minàç, J., Rogelstad, M., and Tân, N. D., Dimensions of Zassenhaus filtration subquotients of some pro-p-groups. Israel J. Math. 212(2016), 825–855.http://dx.doi.Org/10.1007/s11856-016-1310-0 Google Scholar
[31] Neukirch, J., Algebraic number theory. Grundlehren der Mathematischen Wissenschaften, 322,Springer-Verlag, Berlin, 1999. http://dx.doi.Org/10.1007/978-3-662-03983-0 Google Scholar
[32] Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields, Grundlehren der Mathematischen Wissenschaften, 323, Springer-Verlag, Berlin, 2008.http://dx.doi.org/10.1007/978-3-540-37889-1 Google Scholar
[33] Ozaki, M., Construction of maximal unramified p-extensions with prescribed Galois groups. Invent. Math. 183(2011), no. 3, 649–680.http://dx.doi.org/10.1007/s00222-010-0289-0 Google Scholar
[34] Perbet, G., Sur les invariants d'Iwasawa dans les extensions de Lie p-adiques. Algebra Number Theory 5(2011), no. 6, 819–848.http://dx.doi.Org/10.214O/ant.2O11.5.819 Google Scholar
[35] Roquette, P., On class field towers. In: Algebraic Number Theory (Proc. Instructional Conf, Brighton, 1965), Thompson, Washington, D.C., 1967, pp. 231–249.Google Scholar
[36] Schmidt, A., Über pro-p-fundamentalgruppen markierter arithmetischer kurven. J. Reine Angew. Math. 640(2010), 203–235.http://dx.doi.org/10.1515/CRELLE.2010.025 Google Scholar
[37] Serre, J.-P., Cohomologie galoisienne. Lecture Notes in Mathematics, 5, Springer-Verlag,Berlin-New York, 1965.Google Scholar
[38] Tsfasman, M. and Vladut, S., Infinite global fields and the generalized Brauer-Siegel theorem. Mosc. Math. J. 2(2002), no. 2, 329–402.Google Scholar
[39] Venjakob, O., On the structure theory of the Iwasawa algebra of a p-adic Lie group. J. Eur. Math. Soc. (JEMS) 4(2002), 271–311.http://dx.doi.org/10.1007/s100970100038 Google Scholar
[40] Vogel, D., Massey products in the Galois cohomology of number fields, PhD Heidelberg, 2004.Google Scholar
[41] Washington, L. C., Introduction to cyclotomic fields. Graduate Texts in Mathematics, 83, Springer-Verlag, New York, 1999.http://dx.doi.org/10.1007/978-1-4612-1934-7 Google Scholar
[42] Zimmert, R., Ideale kleiner Norm in Idealklasse une eine Regulatorabschatzung. Invent. Math. 62(1981), no. 3, 367–380.http://dx.doi.org/10.1007/BF01394249 Google Scholar