Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:02:31.046Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Integral Extensions of Quadratic Forms Over Local Fields

Published online by Cambridge University Press:  20 November 2018

Melvin Band
Melvin Band*
Affiliation:
Massachusetts Institute of Technology, Cambridge, Massachusetts University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be a local field with ring of integers 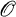and unique prime ideal (p). Suppose that V a finite-dimensional regular quadratic space over F, W and W′ are two isometric subspaces of V (i.e. τ: W → W′ is an isometry from W to W′). By the well-known Witt's Theorem, τ can always be extended to an isometry σ ∈ O(V).

The integral analogue of this theorem has been solved over non-dyadic local fields by James and Rosenzweig [2], over the 2-adic fields by Trojan [4], and partially over the dyadics by Hsia [1], all for the special case that W is a line. In this paper we give necessary and sufficient conditions that two arbitrary dimensional subspaces W and W′ are integrally equivalent over non-dyadic local fields.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 297 - 307
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Hsia, J. S., Integral equivalence of vectors over depleted modular lattices on dyadic local fields, Amer. J. Math. 90 (1968), 285–294.Google Scholar
2. James, D. and Rosenzweig, S., Associated vectors in lattices over valuation rings, Amer. J. Math. 90 (1968), 295–307.Google Scholar
3. O'Meara, O. T., Introduction to quadratic forms, Die Grundlehren der mathematischen Wissenschaften, Bd. 117 (Springer-Verlag, Berlin, 1963).Google Scholar
4. Trojan, A., The integral extension of isometries of quadratic forms over local fields, Can. J. Math. 18 (1966), 920–942.Google Scholar