Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T03:33:15.261Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Global Structure of Special Cycles on Unitary Shimura Varieties

Published online by Cambridge University Press:  20 November 2018

Nicolas Vandenbergen
Nicolas Vandenbergen*
Affiliation:
Mathematisches Institut der Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the reduced loci of special cycles on local models of the Shimura variety for 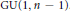$\text{GU}\left( 1,\,n\,-\,1 \right)$. Those special cycles are defined by Kudla and Rapoport. We explicitly compute the irreducible components of the reduced locus of a single special cycle, as well as of an arbitrary intersection of special cycles, and their intersection behaviour in terms of Bruhat–Tits theory. Furthermore, as an application of our results, we prove the connectedness of arbitrary intersections of special cycles, as conjectured by Kudla and Rapoport.

Keywords

14G35Shimura varietieslocal modelsspecial cycles
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 5 , 01 October 2013 , pp. 1125 - 1163
Copyright
Copyright © Canadian Mathematical Society 2013

References

[Ja] Jacobowitz, R., Hermitian forms over local fields. Amer. J. Math. 84(1962), 441–465. http://dx.doi.org/10.2307/2372982 Google Scholar
[KR] Kudla, S. and Rapoport, M., Special cycles on unitary Shimura varieties. I: Unramified local theory. Invent. Math. 184(2011), 629–682.http://dx.doi.org/10.1007/s00222-010-0298-z Google Scholar
[KR2] Kudla, S., Special cycles on unitary Shimura varieties. II: Global theory. arxiv:0912.3758v1Google Scholar
[KR3] Kudla, S., The alternative moduli problem. Unpublished notes, 2010.Google Scholar
[Te] Terstiege, U., Intersections of special cycles on the Shimura variety for GU(1; 2). arxiv:1006.2106Google Scholar
[Te2] Kudla, S., On the regularity of special difference divisors. arxiv:1209.1286Google Scholar
[Ti] Tits, J., Reductive groups over local fields. In: Automorphic forms, representations and L-functions, Proc. Sympos. Pure Math. 33(1979), 29–69.Google Scholar
[Vo] Vollaard, I., The supersingular locus of the Shimura variety for GU(1; s). Canad. J. Math. 62(2010), 668–720. http://dx.doi.org/10.4153/CJM-2010-031-2 Google Scholar
[VW] Vollaard, I. and Wedhorn, T., The supersingular locus of the Shimura variety for GU(1; n − 1) II. Invent. Math. 184(2010), 591–627. http://dx.doi.org/10.1007/s00222-010-0299-y Google Scholar