Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T08:54:25.675Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Geometry of the Moduli Space of Real Binary Octics

Published online by Cambridge University Press:  20 November 2018

Kenneth C. K. Chu
Kenneth C. K. Chu*
Affiliation:
Department of Mathematics, University of Utah, Salt Lake City, Utah, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The moduli space of smooth real binary octics has five connected components. They parametrize the real binary octics whose defining equations have 0, … , 4 complex-conjugate pairs of roots respectively. We show that each of these five components has a real hyperbolic structure in the sense that each is isomorphic as a real-analytic manifold to the quotient of an open dense subset of 5-dimensional real hyperbolic space 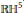$\mathbb{R}{{\mathbb{H}}^{5}}$ by the action of an arithmetic subgroup of Isom$\left( \mathbb{R}{{\mathbb{H}}^{5}} \right)$. These subgroups are commensurable to discrete hyperbolic reflection groups, and the Vinberg diagrams of the latter are computed.

Keywords

32G1332G2014D0514D20real binary octicsmoduli spacecomplex hyperbolic geometryVinberg algorithm
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 4 , 01 August 2011 , pp. 755 - 797
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Allcock, Daniel, Carlson, James A., and Toledo, Domingo, The complex hyperbolic geometry of the moduli space of cubic surfaces. J. Algebraic Geom. 11(2002), 659–724.Google Scholar
[2] Allcock, Daniel, Carlson, James A., Hyperbolic geometry and the moduli space of real binary sextics. In: Arithmetic and geometry around hypergeometric functions, Progr. Math. 260, Birkhäuser, Basel, 2007, 1–22.Google Scholar
[3] Allcock, Daniel, Carlson, James A., Hyperbolic geometry and moduli of real cubic surfaces. Ann. Sci. Ec. Norm. Supér. 43(2010), 69–115.Google Scholar
[4] Chung-kan Chu, Kenneth, The moduli space of real binary octics. Ph.D. dissertation, University of Utah, 2006.Google Scholar
[5] Chern, S. S., Chen, W. H. and Lam, K. S., Lectures on differential geometry. World Scientific Publishing Co. Inc., River Edge, NJ, 1999.Google Scholar
[6] Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J. G. Thackray. Oxford University Press, Eynsham, 1985.Google Scholar
[7] Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and nonlattice integral monodromy. Inst. Hautes Études Sci. Publ. Math. 63(1986), 5–89.Google Scholar
[8] Fox, Ralph H., Covering spaces with singularities. In: A symposium in honor of S. Lefschetz, Princeton University Press, Princeton, NJ, 1957, 243–257.Google Scholar
[9] Gromov, M. and Piatetski-Shapiro, I., Nonarithmetic groups in Lobachevsky spaces. Inst. Hautes Études Sci. Publ. Math. 66(1988), 93–103.Google Scholar
[10] Harris, Joe, Algebraic geometry, A First Course. Graduate Texts in Mathematics 133, Springer-Verlag, New York, 1995.Google Scholar
[11] Kondo, Shigeyuki, The moduli space of 8 points on P1 and automorphic forms. arXiv:math.AG/0504233, 2005, 1–17.Google Scholar
[12] Matsumoto, Keiji and Yoshida, Masaaki, Configuration space of 8 points on the projective line and a 5-dimensional Picard modular group. Compositio Math. 86(1993), 265–280.Google Scholar
[13] Miranda, Rick, Algebraic curves and Riemann surfaces. American Mathematical Society, 1995.Google Scholar
[14] Picard, Émile, Sur les fonctions de deux variables indépendantes analogues aux fonctions modulaires. Acta. Math. 2(1883), 114–135. doi:10.1007/BF02612158Google Scholar
[15] Terada, Toshiaki, Fonctions hypergéométriques F1 et fonctions automorphes. I. J. Math. Soc. Japan 35(1983), 451–475. doi:10.2969/jmsj/03530451Google Scholar
[16] Terada, Toshiaki, Fonctions hypergéométriques F1 et fonctions automorphes. II. Groupes discontinus arithmétiquement définis. J. Math. Soc. Japan 37(1985), 173–185. doi:10.2969/jmsj/03720173Google Scholar
[17] Vinberg, È. B., Some arithmetical discrete groups in Lobacevskii spaces. In: Discrete subgroups of Lie groups and applications to moduli (Internat. Colloq., Bombay, 1973), Oxford University Press, Bombay, 1975, 323–348.Google Scholar