Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:31:44.001Z Has data issue: false hasContentIssue false
  • English
  • Français

On the η Function of Brown and Pearcy and the Numerical Function of an Operator

Published online by Cambridge University Press:  20 November 2018

Norberto Salinas
Norberto Salinas*
Affiliation:
University of Michigan, Ann Arbor, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

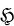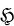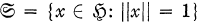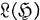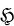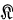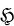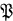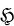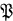Throughout this paper will denote an infinite dimensional, separable complex Hilbert space, and will denote the unit sphere of (i.e. ). Also will represent the algebra of all bounded linear operators on , and will represent the ideal of all compact operators on . Furthermore will denote the set of all (orthogonal) projections on and will denote the sublattice of 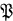consisting of all finite rank projections. In most of the cases (especially when limits are involved) 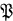will be regarded as a directed set with the usual order relation inherited from .

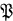Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 565 - 578
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Brown, A. and Pearcy, C., Structure of commutators of operators, Ann. of Math. 82 (1965), 112–127.Google Scholar
2. Dieudonne, J., Foundations of modern analysis (Academic Press, New York, 1960).Google Scholar
3. Douglas, R. G. and Pearcy, C., A characterization of thin operators, Acta Sci. Math. (Szeged.) U (1968), 295–297.Google Scholar
4. Hoover, T. B., Quasi-similarity and hyper invariant subspaces, thesis, University of Michigan (1970).Google Scholar
5. Stampfli, J. G. and Williams, J. P., Growth conditions and the numerical range in aBanach algebra, Tôhoku Math. J. 20 (1968), 417–424 Google Scholar