Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T18:54:43.922Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fractional Parts of a Polynomial

Published online by Cambridge University Press:  20 November 2018

R. J. Cook
R. J. Cook*
Affiliation:
The University of Sheffield, Sheffield, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Heilbronn [6] proved that for any ϵ > 0 there exists C(ϵ) such that for any real θ and N ≧ 1 there is an integer x satisfying

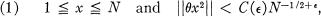
where ||α|| denotes the difference between α and the nearest integer, taken positively. Danicic [2] obtained an analogous result for the fractional parts of θxk and in 1967 Davenport [4] generalized Heilbronn's result to polynomials of degree 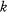with no constant term. The last condition is essential, for if there is a constant term then no analogous result can hold (see Koksma [7, Kap. 6 SatzlO]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 168 - 173
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. C∞k, R. J., On the fractional parts of a set of points, Mathematika 19 (1972), 63–68.Google Scholar
2. Danicic, I., Ph.D. Thesis, University of London, 1957.Google Scholar
3. Davenport, H., Analytic methods for Diophantine equations and Diophantine inequalities (Campus Publishers, Ann Arbor, Michigan, 1962).Google Scholar
4. Davenport, H., On a theorem of Heilbronn, Quart. J. Math. Oxford 18 (1967), 339–344.Google Scholar
5. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, 4th ed. (Oxford, 1965).Google Scholar
6. Heilbronn, H., On the distribution of the sequence n2d (mod 1), Quart. J. Math. Oxford 19 (1948), 249–256.Google Scholar
7. Koksma, J. F., Diophantische Approximationen (Berlin, 1936).Google Scholar
8. Liu, M.-C., On a theorem of Heilbronn concerning the fractional part of 6n2, Can. J. Math. 22 (1970), 784–788.Google Scholar
9. Vinogradov, I. M., The method of trigonometric sums in the theory of numbers (Interscience, New York, 1954).Google Scholar