Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T15:06:27.169Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fourier Transformability of Strongly Almost Periodic Measures

Part of: Abstract harmonic analysis Harmonic analysis in one variable

Published online by Cambridge University Press:  29 January 2019

Nicolae Strungaru
Nicolae Strungaru*
Affiliation:
Department of Mathematical Sciences, MacEwan University, 10700 – 104 Avenue, Edmonton, AB, T5J 4S2 Department of Mathematics, Trent University, Peterborough, ON Institute of Mathematics “Simon Stoilow”, Bucharest, Romania Email: [email protected] URL: http://academic.macewan.ca/strungarun/
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we characterize the Fourier transformability of strongly almost periodic measures in terms of an integrability condition for their Fourier–Bohr series. We also provide a necessary and sufficient condition for a strongly almost periodic measure to be the Fourier transform of a measure. We discuss the Fourier transformability of a measure on 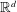$\mathbb{R}^{d}$ in terms of its Fourier transform as a tempered distribution. We conclude by looking at a large class of such measures coming from the cut and project formalism.

Keywords

Fourier transform of measuresalmost periodic measureFourier-Bohr seriesEberlein decomposition

MSC classification

Primary: 43A05: Measures on groups and semigroups, etc.
Secondary: 43A60: Almost periodic functions on groups and semigroups and their generalizations (recurrent functions, distal functions, etc.); almost automorphic functions 43A25: Fourier and Fourier-Stieltjes transforms on locally compact and other abelian groups 42A75: Classical almost periodic functions, mean periodic functions
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 4 , August 2020 , pp. 900 - 927
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argabright, L. N. and Gil de Lamadrid, J., Fourier analysis of unbounded measures on locally compact abelian groups. In: Memoirs of the American Mathematical Society, 145. American Mathematical Society, Providence, RI, 1974.Google Scholar
Aujogue, J.-B., Pure Point/Continuous Decomposition of Translation-Bounded Measures and Diffraction. Ergodic Theory Dynam. Systems, to appear. https://doi.org/10.1017/etds.2018.38Google Scholar
Baake, M. and Grimm, U., Aperiodic order. Vol. 1: A mathematical invitation. Encyclopedia of Mathematics and its Applications, 149, Cambridge University Press, Cambridge, 2013. https://doi.org/10.1017/CBO9781139025256Google Scholar
Baake, M. and Grimm, U., Aperiodic order. Vol. 2: Crystallography and almost periodicity. Encyclopedia of Mathematics and its Applications, 166, Cambridge University Press, Cambridge, 2017. https://doi.org/10.1017/9781139033862Google Scholar
Baake, M. and Lenz, D., Dynamical systems on translation bounded measures: pure point dynamical and diffraction spectra. Ergodic Theory Dynam. Systems 24(2004), 1867–1893. https://doi.org/10.1017/S0143385704000318Google Scholar
Baake, M. and Lenz, D., Deformation of Delone dynamical systems and pure point diffraction. J. Fourier Anal. Appl. 11(2005), 125–150. https://doi.org/10.1007/s00041-005-4021-1Google Scholar
Baake, M. and Lenz, D., Spectral notions of aperiodic order. Discrete Contin. Dyn. Syst. Ser. S 10(2017), 161–190. https://doi.org/10.3934/dcdss.2017009Google Scholar
Baake, M., Lenz, D., and Moody, R. V., A characterisation of model sets via dynamical systems. Ergodic Theory Dynam. Systems 27(2007), 341–382. https://doi.org/10.1017/S0143385706000800Google Scholar
Baake, M. and Moody, R. V., Weighted Dirac combs with pure point diffraction. J. Reine Angew. Math. 573(2004), 61–94. https://doi.org/10.1515/crll.2004.064Google Scholar
Berg, C. and Forst, G., Potential theory on locally compact abelian groups. Springer-Verlag, New York-Heidelberg, 1975.Google Scholar
Bourbaki, N., General topology. parts I and II. Hermann, Paris, 1966.Google Scholar
Bruhat, F., Distributions sur un groupe localement compact et applications à lâĂŹétude des représentations des groupes p-adiques. Bull. Soc. Math. France 89(1961), 43–75.Google Scholar
Eberlein, W. F., Abstract ergodic theorems and weak almost periodic functions. Trans. Amer. Math. Soc. 67(1949), 217–240. https://doi.org/10.2307/1990424Google Scholar
Eberlein, W. F., A note on Fourier–Stiltjes transforms. Proc. Amer. Math. Soc. 6(1955), 310–312. https://doi.org/10.2307/2032365Google Scholar
Eberlein, W. F., The point spectrum of weakly almost periodic functions. Michigan Math. J. 3(1955–56), 137–139.Google Scholar
Favorov, S., Bohr and Besicovitch almost periodic discrete sets and quasicrystals. Proc. Amer. Math. Soc. 140(2012), 1761–1767. https://doi.org/10.1090/S0002-9939-2011-11046-3Google Scholar
Favorov, S., Fourier Quasicrystals and Lagarias’s conjecture. Proc. Amer. Math. Soc. 144(2016), 3527–3536. https://doi.org/10.1090/proc/12979Google Scholar
Lagarias, J. C., Mathematical quasicrystals and the problem of diffraction. In: Directions in mathematical quasicrystals. CRM Monogr. Ser. 13, Amer. Math. Soc., Providence, RI, 2000, pp. 61–93.Google Scholar
Gil. de Lamadrid, J . and Argabright, L. N., Almost periodic measures. Mem. Amer. Math. Soc. 85(1990), no. 428.Google Scholar
Lenz, D., Aperiodic order and pure point diffraction. Philos. Mag. 88(2008), 2059–2071. https://doi.org/10.1080/14786430802082008Google Scholar
Lenz, D. and Richard, C., Pure point diffraction and cut and project schemes for measures: the smooth case. Math. Z. 256(2007), 347–378. https://doi.org/10.1007/s00209-006-0077-0Google Scholar
Lenz, D. and Strungaru, N., Pure point spectrum for measurable dynamical systems on locally compact Abelian groups. J. Math. Pures Appl. 92(2009), 323–341. https://doi.org/10.1016/j.matpur.2009.05.013Google Scholar
Lenz, D. and Strungaru, N., On weakly almost periodic measures. Trans. Amer. Math. Soc. 371(2019), no. 10, 6843–6881. https://doi.org/10.1090/tran/7422Google Scholar
Lin, V., On equivalent norms in the space of square summable entire functions of exponential type. Amer. Math. Soc. Transl. Ser. 2 79(1969), 53–76.Google Scholar
Meyer, Y., Algebraic numbers and harmonic analysis. In: North-Holland Mathematical Library, Vol. 2. North-Holland, Amsterdam, 1972.Google Scholar
Moody, R. V., Meyer sets and their duals. In: The mathematics of long-range aperiodic order (Waterloo, ON, 1995). NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 489, Kluwer Acad. Publ., Dordrecht, 1997, pp. 403–441.Google Scholar
Moody, R. V., Model sets: a survey. In: From quasicrystals to more complex systems. EDP Sciences, Les Ulis, and Springer, Berlin, 2000, pp. 145–166. arxiv:math.MG/0002020Google Scholar
Moody, R. V. and Strungaru, N., Point sets and dynamical systems in the autocorrelation topology. Canad. Math. Bull. 47(2004), 82–99. https://doi.org/10.4153/CMB-2004-010-8Google Scholar
Moody, R. V. and Strungaru, N., Almost periodic measures and their Fourier transforms. In: Aperiodic order. Vol. 2. Encyclopedia Math. Appl., 166, Cambridge Univ. Press, Cambridge, 2017, pp. 173–270.Google Scholar
Pedersen, G. K., Analysis now. Springer, New York, 1989.Google Scholar
Reiter, H., Clasical harmonic analysis and locally compact groups. Clarendon Press, Oxford, 1968.Google Scholar
Reiter, H. and Stegeman, J. D., Clasical harmonic analysis and locally compact groups. In: London Mathematical Society Monographs, 22. The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
Richard, C., Dense Dirac combs in Euclidean space with pure point diffraction. J. Math. Phys. 44(2003), 4436–4449. https://doi.org/10.1063/1.1609032Google Scholar
Richard, C. and Strungaru, N., Pure point diffraction and Poisson summation. Ann. Henri Poincaré 18(2017), 3903–3931. https://doi.org/10.1007/s00023-017-0620-zGoogle Scholar
Richard, C. and Strungaru, N., A short guide to pure point diffraction in cut-and-project sets. J. Phys. A 50(2017), no. 15, 154003. https://doi.org/10.1088/1751-8121/aa5d44Google Scholar
Robertson, A. P. and Thornett, M. L., On translation-bounded measures. J. Austral. Math. Soc. Ser. A 37(1984), 139–142.Google Scholar
Rudin, W., Real and complex analysis. McGraw-Hill, New York, 1987.Google Scholar
Strungaru, N., Almost periodic measures and long-range order in Meyer sets. Discrete Comput. Geom. 33(2005), 483–505. https://doi.org/10.1007/s00454-004-1156-9Google Scholar
Strungaru, N., On the Bragg diffraction spectra of a Meyer set. Canad. J. Math. 65(2013), no. 3, 675–701. https://doi.org/10.4153/CJM-2012-032-1Google Scholar
Strungaru, N., Positive definite measures with discrete Fourier transform and pure point diffraction. Canad. Math. Bull. 54(2011), no. 3, 544–555, 2011.Google Scholar
Strungaru, N., Almost periodic measures and Bragg diffraction. J. Phys. A 46(2013), 125205. https://doi.org/10.1088/1751-8113/46/12/125205Google Scholar
Strungaru, N., On weighted Dirac combs supported inside model sets. J. Phys. A 47(2014), no. 33, 335202. https://doi.org/10.1088/1751-8113/47/33/335202Google Scholar
Strungaru, N., Almost periodic pure point measures. In: Aperiodic order. Vol. 2. Encyclopedia Math. Appl., 166, Cambridge Univ. Press, Cambridge, 2017, pp. 217–342.Google Scholar
Strungaru, N. and Terauds, V., Diffraction theory and almost periodic distributions. J. Stat. Phys. 164(2016), no. 5, 1183–1216. https://doi.org/10.1007/s10955-016-1579-8Google Scholar
Thornett, M. L., A class of second-order stationary random measures. Stochastic Process. Appl. 8(1979), 323–334. https://doi.org/10.1016/0304-4149(79)90007-3Google Scholar