Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T07:07:07.487Z Has data issue: false hasContentIssue false
  • English
  • Français

On the First Zassenhaus Conjecture and Direct Products

Part of: Rings and algebras arising under various constructions Conditions on elements Representation theory of groups

Published online by Cambridge University Press:  15 October 2018

Andreas Bächle ,
Wolfgang Kimmerle  and
Mariano Serrano
Andreas Bächle
Affiliation:
Vakgroep Wiskunde, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium Email: [email protected]
Wolfgang Kimmerle
Affiliation:
Fachbereich Mathematik, IGT, Universität Stuttgart, Pfaffenwaldring 57, 70550 Stuttgart, Germany Email: [email protected]
Mariano Serrano
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, 30100, Murcia, Spain Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the behavior of the first Zassenhaus conjecture (ZC1) under direct products, as well as the General Bovdi Problem (Gen-BP), which turns out to be a slightly weaker variant of (ZC1). Among other things, we prove that (Gen-BP) holds for Sylow tower groups, and so in particular for the class of supersolvable groups.

(ZC1) is established for a direct product of Sylow-by-abelian groups provided the normal Sylow subgroups form together a Hall subgroup. We also show (ZC1) for certain direct products with one of the factors a Frobenius group.

We extend the classical HeLP method to group rings with coefficients from any ring of algebraic integers. This is used to study (ZC1) for the direct product 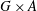$G\times A$, where 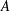$A$ is a finite abelian group and 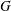$G$ has order at most 95. For most of these groups we show that (ZC1) is valid and for all of them that (Gen-BP) holds. Moreover, we also prove that (Gen-BP) holds for the direct product of a Frobenius group with any finite abelian group.

Keywords

integral group ringtorsion unitZassenhaus Conjecturedirect productFrobenius groupHeLP method

MSC classification

Primary: 16S34: Group rings , Laurent polynomial rings
Secondary: 16U60: Units, groups of units 20C05: Group rings of finite groups and their modules
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 3 , June 2020 , pp. 602 - 624
Copyright
© Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is a postdoctoral researcher of the FWO (Research Foundation Flanders). The third author has been partially supported by the Spanish Government under Grant MTM2016-77445-P with “Fondos FEDER” and by Fundación Séneca of Murcia under Grant 19880/GERM/15.

References

Mini-Workshop: Arithmetik von Gruppenringen: Abstracts from the mini-workshop held November 25–December 1, 2007. Oberwolfach Rep. 4(2007), no. 4, 3209–3239. https://www.mfo.de/occasion/0748c/www_view.Google Scholar
Bächle, A., Herman, A., Konovalov, A., Margolis, L., and Singh, G., The status of the Zassenhaus conjecture for small groups. Experiment. Math. 27(2018), no. 4, 431–436. https://doi.org/10.1080/10586458.2017.1306814.Google Scholar
Bächle, A., Kimmerle, W., and Margolis, L., Algorithmic aspects of units in group rings. In: Algorithmic and experimental methods in algebra, geometry, and number theory. Springer, Cham, 2018, pp. 1–22.Google Scholar
Bächle, A. and Margolis, L., HeLP: A GAP package for torsion units in integral group rings. J. Softw. Algebra Geom 8(2018), 1–9. https://doi.org/10.2140/jsag.2018.8.1.Google Scholar
Bächle, A. and Margolis, L., Rational conjugacy of torsion units in integral group rings of non-solvable groups. Proc. Edinb. Math. Soc. (2) 60(2017), 813–830. https://doi.org/10.1017/S0013091516000535.Google Scholar
Bovdi, A. A., The unit group of an integral group ring (Russian). Uzhgorod Univ. Uzhgorod 1987.Google Scholar
Bovdi, V. A. and Hertweck, M., Zassenhaus conjecture for central extensions of S 5. J. Group Theory 11(2008), 63–74. https://doi.org/10.1515/JGT.2008.004.Google Scholar
Caicedo, M., Margolis, L., and del Rio, Á., Zassenhaus conjecture for cyclic-by-abelian groups. J. Lond. Math. Soc. (2) 88(2013), no. 1, 65–78. https://doi.org/10.1112/jlms/jdt002.Google Scholar
Cheng, K. N., Deaconescu, M., Lang, M., and Shi, W. J., Corrigendum and addendum to: “Classification of finite groups with all elements of prime order” [Proc. Amer. Math. Soc. 106 (1989), no. 3, 625–629; MR0969518 (89k:20038)] by Deaconescu. Proc. Amer. Math. Soc. 117(1993), 1205–1207.Google Scholar
Cohn, J. A. and Livingstone, D., On the structure of group algebras. I. Canad. J. Math. 17(1965), 583–593. https://doi.org/10.4153/CJM-1965-058-2.Google Scholar
Dark, R. and Scoppola, C. M., On Camina group of prime power order. J. Algebra 181(1996), 787–802. https://doi.org/10.1006/jabr.1996.0146.Google Scholar
Dokuchaev, M. A. and Juriaans, S. O., Finite subgroups in integral group rings. Canad. J. Math. 48(1996), 1170–1179. https://doi.org/10.4153/CJM-1996-061-7.Google Scholar
Dokuchaev, M. A. and Sehgal, S. K., Torsion units in integral group rings of solvable groups. Comm. Algebra 22(1994), no. 12, 5005–5020. https://doi.org/10.1080/00927879408825118.Google Scholar
Dokuchaev, M. A., Juriaans, S. O., and Polcino Milies, C., Integral group rings of Frobenius groups and the conjectures of H. J. Zassenhaus. Comm. Algebra 25(1997), 2311–2325.Google Scholar
Eisele, F. and Margolis, L., A counterexample to the first Zassenhaus conjecture. Adv. Math. 339(2018), 599–641. https://doi.org/10.1016/j.aim.2018.10.004.Google Scholar
The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.8.3. 2016. http://www.gap-system.org.Google Scholar
Hertweck, M., Torsion units in integral group rings of certain metabelian groups. Algebra Colloq. 13(2006), 329–348. https://doi.org/10.1142/S1005386706000290.Google Scholar
Hertweck, M., Partial augmentations and Brauer character values of torsion units in group rings. 2007. arxiv:0612429v2.Google Scholar
Hertweck, M., Torsion units in integral group rings of certain metabelian groups. Proc. Edinb. Math. Soc. (2) 51(2008), no. 2, 363–385. https://doi.org/10.1017/S0013091505000039.Google Scholar
Hertweck, M., The orders of torsion units in integral group rings of finite solvable groups. Comm. Algebra 36(2008), no. 10, 3585–3588. https://doi.org/10.1080/00927870802157632.Google Scholar
Hertweck, M., On torsion units in integral group rings of Frobenius groups. arxiv:1207.5256v1.Google Scholar
Höfert, C., Die erste Vermutung von Zassenhaus für Gruppen kleiner Ordnung. Diplomarbeit, University of Stuttgart, 2004.Google Scholar
Höfert, C. and Kimmerle, W., On torsion units of integral group rings of groups of small order. In: Groups, rings and group rings. Lect. Notes Pure Appl. Math., 248, Chapman & Hall/CRC, Boca Raton, FL, 2006, pp. 243–252. https://doi.org/10.1201/9781420010961.ch23.Google Scholar
Huppert, B., Endliche Gruppen I. Die Grundlehren der Mathematischen Wissenschaften, 134, Springer-Verlag, Berlin, 1967.Google Scholar
Isaacs, I. M. and Lewis, M., Camina p-groups that are generalized Frobenius complements. Arch. Math. (Basel) 104(2015), 401–405. https://doi.org/10.1007/s00013-015-0755-4.Google Scholar
Juriaans, S. O. and Milies, C. P., Units of integral group rings of Frobenius groups. J. Group Theory 3(2000), 277–284. https://doi.org/10.1515/jgth.2000.022.Google Scholar
Kimmerle, W. and Margolis, L., p-subgroups of units in ℤG. In: Groups, rings, group rings, and Hopf algebras. Contemp. Math., 688, Amer. Math. Soc., Providence, RI, 2017, pp. 169–179.Google Scholar
Lewis, M., Classifying Camina groups: a theorem of Dark and Scoppola. Rocky Mountain J. Math. 44(2014), 591–597. https://doi.org/10.1216/RMJ-2014-44-2-591.Google Scholar
Luthar, I. S. and Passi, I. B. S., Zassenhaus conjecture for A 5. Proc. Indian Acad. Sci. Math. Sci. 99(1989), 1–5. https://doi.org/10.1007/BF02874643.Google Scholar
Luthar, I. S. and Trama, P., Zassenhaus conjecture for S 5. Comm. Algebra 19(1991), no. 8, 2353–2362. https://doi.org/10.1080/00927879108824263.Google Scholar
Marciniak, Z., Ritter, J., Sehgal, S. K., and Weiss, A., Torsion units in integral group rings of some metabelian groups. II. J. Number Theory 25(1987), 340–352. https://doi.org/10.1016/0022-314X(87)90037-0.Google Scholar
Margolis, L., A theorem of Hertweck on p-adic conjugacy of p-torsion units in group rings. 2017. arxiv:1706.02117v1.Google Scholar
Margolis, L. and del Río, Á., Partial augmentations property: A Zassenhaus conjecture related problem. J. Pure Appl. Algebra, in print, 2018. https://doi.org/10.1016/j.jpaa.2018.12.018.Google Scholar
Passman, D., Permutation groups. W. A. Benjamin, Inc., New York–Amsterdam, 1968.Google Scholar
del Río, Á. and Serrano, M., On the torsion units of the integral group ring of finite projective special linear groups. Comm. Algebra 45(2017), no. 12, 5073–5087. https://doi.org/10.1080/00927872.2017.1291814.Google Scholar
Sehgal, S. K., Units in integral group rings. Pitman Monographs and Surveys in Pure and Applied Mathematics, 69, Longman Scientic & Technical, Harlow; John Wiley & Sons, New York, 1993.Google Scholar
Weiss, A., Torsion units in integral group rings. J. Reine Angew. Math. 415(1991), 175–187. https://doi.org/10.1515/crll.1991.415.175.Google Scholar
Weiss, E., Algebraic number theory. McGraw-Hill Book Co., Inc., New York–San Francisco–Toronto–London, 1963.Google Scholar
Zassenhaus, H., On the torsion units of finite group rings, Studies in mathematics (in honor of A. Almeida Costa) (Portuguese). Instituto de Alta Cultura, Lisbon, 1974, pp. 119–126.Google Scholar