Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T23:00:35.251Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Finiteness length of some soluble linear groups

Part of: Other groups of matrices Special aspects of infinite or finite groups Low-dimensional topology Linear algebraic groups and related topics

Published online by Cambridge University Press:  21 April 2021

Yuri Santos Rego
Yuri Santos Rego*
Affiliation:
Faculty of Mathematics, Bielefeld University, BielefeldGermany Current address: Institute of Algebra and Geometry, Otto von Guericke University Magdeburg, Magdeburg, Germany
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a commutative unital ring R, we show that the finiteness length of a group G is bounded above by the finiteness length of the Borel subgroup of rank one 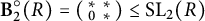$\textbf {B}_2^{\circ }(R)=\left ( \begin {smallmatrix} * & * \\ 0 & * \end {smallmatrix}\right )\leq \operatorname {\textrm {SL}}_2(R)$ whenever G admits certain R-representations with metabelian image. Combined with results due to Bestvina–Eskin–Wortman and Gandini, this gives a new proof of (a generalization of) Bux’s equality on the finiteness length of S-arithmetic Borel groups. We also give an alternative proof of an unpublished theorem due to Strebel, characterizing finite presentability of Abels’ groups 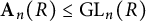$\textbf {A}_n(R) \leq \operatorname {\textrm {GL}}_n(R)$ in terms of n and 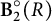$\textbf {B}_2^{\circ }(R)$ . This generalizes earlier results due to Remeslennikov, Holz, Lyul’ko, Cornulier–Tessera, and points out to a conjecture about the finiteness length of such groups.

Keywords

Finiteness propertiessoluble group schemesS-arithmetic groupsAbels’ groups

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20H25: Other matrix groups over rings 20F05: Generators, relations, and presentations 20G30: Linear algebraic groups over global fields and their integers 57M07: Topological methods in group theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 5 , October 2022 , pp. 1209 - 1243
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work was supported by the Deutscher Akademischer Austauschdienst (Förder-ID 57129429) and the Bielefelder Nachwuchsfonds.

References

Abels, H., An example of a finitely presented solvable group . In: Homological group theory (Proceedings Symposium Durham, 1977), London Mathematics Society Lecture Notes Series, 36, Cambridge University Press, Cambridge, MA, New York, NY, 1979, pp. 205–211. http://doi.org/10.1017/CBO9781107325449.008 Google Scholar
Abels, H., Finite presentability of S-arithmetic groups. Compact presentability of solvable groups. Lecture Notes in Mathematics, 1261, Springer-Verlag, Berlin, Germany, 1987. http://doi.org/10.1007/BFb0079708 CrossRefGoogle Scholar
Abels, H. and Brown, K. S., Finiteness properties of solvable $\, S$ -arithmetic groups: An example . J. Pure Appl. Algebra 44(1987), nos. 1–3, 77–83. http://doi.org/10.1016/0022-4049(87)90016-8 CrossRefGoogle Scholar
Abels, H. and Holz, S., Higher generation by subgroups. J. Algebra 160(1993), no. 2, 310–341. http://doi.org/10.1006/jabr.1993.1190 CrossRefGoogle Scholar
Abramenko, P. and Brown, K. S., Buildings. Theory and applications. Graduate Texts in Mathematics, 248, Springer, New York, NY, 2008. http://doi.org/10.1007/978-0-387-78835-7 Google Scholar
Alonso, J. M., Finiteness conditions on groups and quasi-isometries. J. Pure Appl. Algebra 95(1994), no. 2, 121–129. http://doi.org/10.1016/0022-4049(94)90069-8 CrossRefGoogle Scholar
Baumgartner, U. and Willis, G. A., Contraction groups and scales of automorphisms of totally disconnected locally compact groups. Israel J. Math. 142(2004), 221–248. http://doi.org/10.1007/BF02771534 CrossRefGoogle Scholar
Becker, O., Lubotzky, A., and Thom, A., Stability and invariant random subgroups. Duke Math. J. 168(2019), no. 12, 2207–2234. http://doi.org/10.1215/00127094-2019-0024 CrossRefGoogle Scholar
Behr, H., Arithmetic groups over function fields. I. A complete characterization of finitely generated and finitely presented arithmetic subgroups of reductive algebraic groups. J. Reine Angew. Math. 495(1998), 79–118. http://doi.org/10.1515/crll.1998.023 CrossRefGoogle Scholar
Benli, M. G., Grigorchuk, R., and de la Harpe, P., Amenable groups without finitely presented amenable covers. Bull. Math. Sci. 3(2013), no. 1, 73–131. http://doi.org/10.1007/s13373-013-0031-5 Google Scholar
Bestvina, M., Eskin, A., and Wortman, K., Filling boundaries of coarse manifolds in semisimple and solvable arithmetic groups. J. Eur. Math. Soc. (JEMS) 15(2013), no. 6, 2165–2195. http://doi.org/10.4171/JEMS/419 CrossRefGoogle Scholar
Bieri, R., A connection between the integral homology and the centre of a rational linear group. Math. Z. 170(1980), no. 3, 263–266. http://doi.org/10.1007/BF01214865 CrossRefGoogle Scholar
Bieri, R., de Cornulier, Y., Guyot, L., and Strebel, R., Infinite presentability of groups and condensation. J. Inst. Math. Jussieu 13(2014), no. 4, 811–848. http://doi.org/10.1017/S1474748013000327 CrossRefGoogle Scholar
Bieri, R. and Strebel, R., Valuations and finitely presented metabelian groups. Proc. Lond. Math. Soc. (3) 41(1980), no. 3, 439–464. http://doi.org/10.1112/plms/s3-41.3.439 Google Scholar
Borel, A. and Serre, J.-P., Cohomologie d'immeubles et de groupes $\, S$ -arithmétiques . Topology 15(1976), no. 3, 211–232. http://doi.org/10.1016/0040-9383(76)90037-9 CrossRefGoogle Scholar
Bridson, M. R., Howie, J., Miller, C. F. III, and Short, H., On the finite presentation of subdirect products and the nature of residually free groups. Amer. J. Math. 135(2013), no. 4, 891–933. http://doi.org/10.1353/ajm.2013.0036 CrossRefGoogle Scholar
Brown, K. S., Presentations for groups acting on simply-connected complexes. J. Pure Appl. Algebra 32(1984), no. 1, 1–10. http://doi.org/10.1016/0022-4049(84)90009-4 CrossRefGoogle Scholar
Brown, K. S., Finiteness properties of groups. J. Pure Appl. Algebra 44(1987), nos. 1–3, 45–75. http://doi.org/10.1016/0022-4049(87)90015-6 CrossRefGoogle Scholar
Brück, B., Higher generating subgroups and Cohen–Macaulay complexes. Proc. Edinb. Math. Soc. 63(2020), no. 1, 275–285. http://doi.org/10.1017/S0013091519000415 CrossRefGoogle Scholar
Brück, B., Between buildings and free factor complexes: A Cohen–Macaulay complex for Out(RAAGs). Preprint, arXiv:1906.05606v1, 2019. https://arxiv.org/pdf/1906.05606v1.pdf Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. Inst. Hautes Études Sci. Publ. Math. 41(1972), 5–251. http://doi.org/10.1007/BF02715544 CrossRefGoogle Scholar
Bux, K.-U., Finiteness properties of soluble arithmetic groups over global function fields. Geom. Topol. 8(2004), 611–644. http://doi.org/10.2140/gt.2004.8.611 Google Scholar
Bux, K.-U., Higher finiteness properties of braided groups . In: Baake, M., Götze, F., and Hoffmann, W. (eds.), Spectral Structures and Topological Methods in Mathematics, EMS Publishing House, Zurich, Switzerland, p. 2019. http://doi.org/10.4171/197-1/13 Google Scholar
Bux, K.-U., Fluch, M. G., Marschler, M., Witzel, S., and Zaremsky, M. C. B., The braided Thompson's groups are of type $\, {F}_{\infty }$ . J. Reine Angew. Math. 718(2016), 59–101. http://doi.org/10.1515/crelle-2014-0030. With an appendix by Zaremsky.CrossRefGoogle Scholar
Bux, K.-U., Köhl, R., and Witzel, S., Higher finiteness properties of reductive arithmetic groups in positive characteristic: the rank theorem. Ann. Math. (2) 177(2013), no. 1, 311–366. http://doi.org/10.4007/annals.2013.177.1.6 CrossRefGoogle Scholar
Bux, K.-U., Mohammadi, A., and Wortman, K., ${SL}_n\left(\mathbb{Z}\left[t\right]\right)\,$ is not $\, {FP}_{n-1}$ . Comment. Math. Helv. 85(2010), no. 1, 151–164. http://doi.org/10.4171/CMH/191 CrossRefGoogle Scholar
Bux, K.-U. and Wortman, K., Finiteness properties of arithmetic groups over function fields. Invent. Math. 167(2007), no. 2, 355–378. http://doi.org/10.1007/s00222-006-0017-y CrossRefGoogle Scholar
Carrión, J. R., Dadarlat, M., and Eckhardt, C., On groups with quasidiagonal $\, {C}^{\ast }$ -algebras . J. Funct. Anal. 265(2013), no. 1, 135–152. http://doi.org/10.1016/j.jfa.2013.04.004 CrossRefGoogle Scholar
Carter, R. W., Simple groups of Lie type Pure and Applied Mathematics, 28, John Wiley & Sons, London-New York-Sydney, 1972.Google Scholar
Charney, R. and Davis, M. W., The $\, K\left(\pi, 1\right)$ -problem for hyperplane complements associated to infinite reflection groups . J. Amer. Math. Soc. 8(1995), no. 3, 597–627. http://doi.org/10.2307/2152924 Google Scholar
de Cornulier, Y., Guyot, L., and Pitsch, W., On the isolated points in the space of groups. J. Algebra 307(2007), no. 1, 254–277. http://doi.org/10.1016/j.jalgebra.2006.02.012 CrossRefGoogle Scholar
de Cornulier, Y. and Tessera, R., Dehn function and asymptotic cones of Abels' group. J. Topol. 6(2013), no. 4, 982–1008. http://doi.org/10.1112/jtopol/jtt019 CrossRefGoogle Scholar
Demazure, M. and Grothendieck, A., Schemas en Groupes. Tome III: Structure des Schemas en Groupes Reductifs (Séminaire de Géometrie Algébrique du Bois Marie 1962/1964 SGA3), Lecture Notes in Mathematics, 153, Springer-Verlag, Berlin-Heidelberg, 1970. http://doi.org/10.1007/BFb0059027 Google Scholar
Devillers, A. and Mühlherr, B., On the simple connectedness of certain subsets of buildings. Forum Math. 19(2007), no. 6, 955–970. http://doi.org/10.1515/FORUM.2007.037 CrossRefGoogle Scholar
Dieudonné, J., On simple groups of type ${B}_n$ . Amer. J. Math. 79(1957), 922–923. http://doi.org/10.2307/2372442 CrossRefGoogle Scholar
Gandini, G., Bounding the homological finiteness length. Bull. Lond. Math. Soc. 44(2012), no. 6, 1209–1214. http://doi.org/10.1112/blms/bds047 CrossRefGoogle Scholar
Geoghegan, R., Topological methods in group theory. Graduate Texts in Mathematics, 243, Springer, New York, NY, 2008. http://doi.org/10.1007/978-0-387-74614-2 CrossRefGoogle Scholar
Hahn, A. J. and O'Meara, O. T., The classical groups and K-theory. Grundlehren der Mathematischen Wissenschaften, 291, Springer-Verlag, Berlin, Germany, 1989. http://doi.org/10.1007/978-3-662-13152-7 CrossRefGoogle Scholar
Holz, S., Endliche Identifizierbarkeit von Gruppen. PhD thesis, Universität Bielefeld, Germany, 1985.Google Scholar
Kochloukova, D. H., The FPm conjecture for a class of metabelian groups. J. Algebra 184(1996), no. 3, 1175–1204. http://doi.org/10.1006/jabr.1996.0306 CrossRefGoogle Scholar
Kropholler, P. H., and Mullaney, J. P., Homological finiteness conditions for a class of metabelian groups. Bull. Lond. Math. Soc. 50(2018), no. 1, 17–25. http://doi.org/10.1112/blms.12093 CrossRefGoogle Scholar
Lyul'ko, A. N., A family of solvable linear groups that do not satisfy the maximal condition on normal subgroups. Mat. Zametki 39(1986), no. 4, 507–511, 621. http://doi.org/10.1007/BF01157997 Google Scholar
Margulis, G. A., Discrete subgroups of semisimple Lie groups. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 17, Springer-Verlag, Berlin, Germany, 1991. http://doi.org/10.1007/978-3-642-51445-6 CrossRefGoogle Scholar
Meier, J., Meinert, H., and VanWyk, L., Higher generation subgroup sets and the $\, \varSigma$ -invariants of graph groups . Comment. Math. Helv. 73(1998), no. 1, 22–44. http://doi.org/10.1007/s000140050044 Google Scholar
O'Meara, O. T., On the finite generation of linear groups over Hasse domains. J. Reine Angew. Math. 217(1965), 79–108. http://doi.org/10.1515/crll.1965.217.79 CrossRefGoogle Scholar
Ratcliffe, J. G., Finiteness conditions for groups. J. Pure Appl. Algebra 27(1983), no. 2, 173–185. http://doi.org/10.1016/0022-4049(83)90013-0 CrossRefGoogle Scholar
Ree, R., Construction of certain semi-simple groups. Canad. J. Math. 16(1964), 490–508. http://doi.org/10.4153/CJM-1964-051-6 CrossRefGoogle Scholar
Santos Rego, Y., Finiteness properties of split extensions of linear groups. PhD thesis, Universität Bielefeld, Germany, 2019. https://doi.org/10.4119/unibi/2937569 CrossRefGoogle Scholar
Samuel, P., Algebraic theory of numbers. Houghton Mifflin Co., Boston, MA, 1970.Google Scholar
Seligman, G. B., On automorphisms of Lie algebras of classical type. II. Trans. Amer. Math. Soc. 94(1960), 452–482. http://doi.org/10.2307/1993434 CrossRefGoogle Scholar
Serre, J.-P., Trees. Springer-Verlag, Berlin, New York, 1980. http://doi.org/10.1007/978-3-642-61856-7 CrossRefGoogle Scholar
Skipper, R., Witzel, S., and Zaremsky, M. C. B., Simple groups separated by finiteness properties. Invent. Math. 215(2019), no. 2, 713–740. http://doi.org/10.1007/s00222-018-0835-8 CrossRefGoogle Scholar
Steinberg, R., Lectures on Chevalley groups. University Lecture Series, 66, American Mathematical Society, Providence, RI, 2016. http://doi.org/10.1090/ulect/066 CrossRefGoogle Scholar
Strebel, R., Some finitely presented, soluble matrix groups. Manuscript, 14 pages, 1978.Google Scholar
Tiemeyer, A., A local-global principle for finiteness properties of $\ S$ -arithmetic groups over number fields . Transform. Groups 2(1997), no. 2, 215–223. http://doi.org/10.1007/BF01235942 CrossRefGoogle Scholar
Tits, J., Buildings of spherical type and finite BN-pairs. Lecture Notes in Mathematics, 386, Springer-Verlag, Berlin-New York, NY, 1974. http://doi.org/10.1007/978-3-540-38349-9 Google Scholar
Tits, J., Ensembles ordonnés, immeubles et sommes amalgamées. Bull. Soc. Math. Belg. Sér. A 38(1986), 367–387.Google Scholar
Vavilov, N. A. and Plotkin, E., Chevalley groups over commutative rings. I. Elementary calculations. Acta Appl. Math. 45(1996), no. 1, 73–113. http://doi.org/10.1007/BF00047884 CrossRefGoogle Scholar
Witzel, S., Abels's groups revisited. Algebr. Geom. Topol. 13(2013), no. 6, 3447–3467. http://doi.org/10.2140/agt.2013.13.3447 CrossRefGoogle Scholar