Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
David, John E.
1976.
On a retract of an integral domain.
Manuscripta Mathematica,
Vol. 19,
Issue. 3,
p.
245.
Lu, Fangyan
2006.
Lie derivations of certain CSL algebras.
Israel Journal of Mathematics,
Vol. 155,
Issue. 1,
p.
149.
Li, Pengtong
and
Li, Fengjie
2012.
Jordan Modules and Jordan Ideals of Reflexive Algebras.
Integral Equations and Operator Theory,
Vol. 74,
Issue. 1,
p.
123.
QI, XIAOFEI
2017.
Lie n-derivations on
J
$ {\mathcal {J}}$
-subspace lattice algebras.
Proceedings - Mathematical Sciences,
Vol. 127,
Issue. 3,
p.
537.


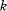 . Suppose there is a subring
. Suppose there is a subring 