Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T17:15:46.706Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Distribution of nθ Modulo 1

Published online by Cambridge University Press:  20 November 2018

R. L. Graham  and
J. H. Van Lint
R. L. Graham
Affiliation:
Bell Telephone Laboratories, Murray Hill, N.J.
J. H. Van Lint
Affiliation:
Technological University, Eindhoven, The Netherlands
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In recent work of E. Arthurs and L. A. Shepp on a problem of H. Dym concerning the existence of an ergodic stationary stochastic process with zero entropy (cf. 1), the function dθ(n) was introduced as follows:

For an irrational number θ, let

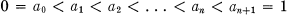
be the sequence of points {lθ}, 1 ≦ l ≦ n, (where {x} denotes x — [x], the fractional part of x) and define*

dθ(n) = max(ai — ai-1), 1 ≦ in + 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 1020 - 1024
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

It should be noted that the related function d′θ(n) = min1≤i≤n+1(ai — ai-1) has been extensively studied by Sόs, Halton, and others (cf. 2; 4; 5; 6; 7; 8; and 9).

References

1. Dym, H., On the structure and the Hausdorff dimension of the support of a class of distribution functions induced by ergodic sequences, Mitre Corp., T.M.-4155 (1965).10.21236/AD0623616CrossRefGoogle Scholar
2. Halton, J. H., The distribution of the sequence {n%\ (n = 0, 1, 2, …), Proc. Cambridge Philos. Soc. 61 (1965), 665–670.Google Scholar
3. Khinchin, A. Ya., Continued fractions (Univ. Chicago Press, Chicago, 1964).Google Scholar
4. Ostrowski, A., Bemerkungen zur Théorie der diophantischen Approximationen, Abh. Math. Sem. Univ. Hamburg 1 (1921), 77–98.Google Scholar
5. Sόs, Vera T., On the theory of diophantine approximations. I, Acta Math. VIII (1957), 461–472.10.1007/BF02020329CrossRefGoogle Scholar
6. Sόs, Vera T., On the distribution Mod 1 of the sequence na, Ann. Univ. Sci. Budapest. Eôtvôs Sect. Math. 1 (1958), 127–134.Google Scholar
7. Slater, N. B., The distribution of the integer N for which {ON}, Proc. Cambridge Philos. Soc. 46 (1950), 525–537.Google Scholar
8. Surányi, J., Uber die Anordnung der Vielfachen einer reellen Zahl mod 1, Ann. Univ. Sci. Budapest. Eôtvôs Sect. Math. 1 (1958), 107–111.Google Scholar
9. Swierczkowski, S., On successive settings of an arc on the circumference of a circle, Fund. Math. 46 (1958), 187–189.Google Scholar