Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T16:49:40.937Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Diameter of a p-Cyclic Strongly Connected Digraph

Published online by Cambridge University Press:  20 November 2018

M. Stuart Lynn
M. Stuart Lynn*
Affiliation:
I.B.M. Scientific Center, 6900 Fannin, Houston, Texas 77025, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we follow the notation of (2). In (5), Luce showed, in other terminology, that if d is the diameter of a strongly connected digraph, D, on n vertices with m edges, then

1.1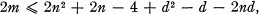

this inequality being sharp; from (1.1) one may immediately derive sharp upper bounds for d in terms of m and n, this being a generalization of the obvious and well-known inequality

1.2

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 749 - 755
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Berge, C., The theory of graphs (Methuen, London, 1962).Google Scholar
2. Harary, F., Norman, R., and Cartwright, D., Structural models and introduction to the theory of directed graphs (Wiley, New York, 1965).Google Scholar
3. Heap, B. R. and Lynn, M. S., The index of primitivity of a non-negative matrix, Numer. Math., 6 (1964), 120–141.Google Scholar
4. Heap, B. R. and Lynn, M. S., To structure of powers of a non-negative matrix. I. The index of convergence, J. Soc. Indust. Appl. Math., 12 (1966).Google Scholar
5. Luce, R. D., Connectivity and generalized cliques in sociometric group structure, Psychometrika, 15 (1950), 169–190.Google Scholar