Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goenner, Hubert F. M.
2014.
On the History of Unified Field Theories. Part II. (ca. 1930–ca. 1965).
Living Reviews in Relativity,
Vol. 17,
Issue. 1,


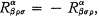
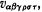 antisymmetric in α, β, γ, and in ρ,σ, into five irreducible parts. This decomposition can be applied to the R of Einstein if we define the tensor v by
antisymmetric in α, β, γ, and in ρ,σ, into five irreducible parts. This decomposition can be applied to the R of Einstein if we define the tensor v by