Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T07:08:19.830Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Class-Number of the Maximal Real Subfield of a Cyclotomic Field

Published online by Cambridge University Press:  20 November 2018

Hiroshi Takeuchi
Hiroshi Takeuchi*
Affiliation:
Tokyo Metropolitan Agricultural Senior High School, Tokyo, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be an integer and let H(p) be the class-number of the field

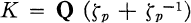
where ζp is a primitive p-th root of unity and Q is the field of rational numbers. It has been proved in [1] that if p = (2qn)2 + 1 is a prime, where q is a prime and n > 1 an integer, then H(p) > 1. Later, S. D. Lang [2] proved the same result for the prime number p = ((2n + 1)q)2 + 4, where q is an odd prime and n ≧ 1 an integer. Both results have been obtained in the case p ≡ 1 (mod 4).

In this paper we shall prove the similar results for a certain prime number p ≡ 3 (mod 4).

We designate by h(p) the class-number of the real quadratic field

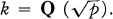
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 55 - 58
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Ankeny, N. C., Chowla, S. and Hasse, H., On the class-number of the maximal real subfield of a cyclotomic field, J. reine angew. Math. 217 (1965), 217–220.Google Scholar
2. Lang, S. D., Note on the class-number of the maximal real subfield of a cyclotomic field, J. reine angew. Math. 290 (1977), 70–72.Google Scholar
3. Yamaguchi, I., On the class-number of the maximal real subfield of a cyclotomic field, J. reine angew. Math. 272 (1975), 217–220.Google Scholar
4. Yamaguchi, I. and Oozeki, K., On the class-number of the real quadratic field, T R U (Tokyo Rika University) Mathematics 8 (1972), 13–14.Google Scholar