Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T06:12:18.377Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Bragg Diffraction Spectra of a Meyer Set

Published online by Cambridge University Press:  20 November 2018

Nicolae Strungaru
Nicolae Strungaru*
Affiliation:
Department of Mathematical Sciences, Grant MacEwan University, Edmonton, AB, T5J 4S2 Institute of Mathematics “Simon Stoilow”, Bucharest, Romania, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Meyer sets have a relatively dense set of Bragg peaks, and for this reason they may be considered as basic mathematical examples of (aperiodic) crystals. In this paper we investigate the pure point part of the diffraction of Meyer sets in more detail. The results are of two kinds. First, we show that, given a Meyer set and any positive intensity 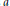$a$ less than the maximum intensity of its Bragg peaks, the set of Bragg peaks whose intensity exceeds 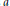$a$ is itself a Meyer set (in the Fourier space). Second, we show that if a Meyer set is modified by addition and removal of points in such a way that its density is not altered too much (the allowable amount being given explicitly as a proportion of the original density), then the newly obtained set still has a relatively dense set of Bragg peaks.

Keywords

52C23diffractionMeyer setBragg peaks
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 3 , 01 June 2013 , pp. 675 - 701
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Argabright, L. N. and Gil., J. Lamadrid, de, Fourier analysis of unbounded measures on locally compact abelian groups. Mem. Amer. Math. Soc. 145, 1974.Google Scholar
[2] N Argabright, L., On the mean of a weakly almost periodic function. Proc. Amer. Math. Soc. 36(1972), 315–316.Google Scholar
[3] Baake, M. andLenz, D., Dynamical systems on translation bounded measures: Pure point dynamical and diffraction spectra. Ergodic Theory Dynam. Systems 24(2004), 1867–1893. math.DS/0302061 http://dx.doi.org/10.1017/S0143385704000318 Google Scholar
[4] Baake, M., Lenz, D., and Moody, R. V., Characterisation of model sets by dynamical systems. Ergodic Theory Dynam. Systems 27(2007), 341–382. math.DS/0511648 http://dx.doi.org/10.1017/S0143385706000800 Google Scholar
[5] Baake, M. and Moody, R. V., Weighted Dirac combs with pure point diffraction. Crelle J., 2004. math.MG/0203030 http://dx.doi.org/10.1515/crll.2004.064 Google Scholar
[6] Berg, C. and Forst, G., Potential theory on locally compact abelian group. Springer-Verlag, Berlin–Heidelberg, 1975.Google Scholar
[7] A.Cordoba, , Dirac combs. Lett. Math. Phys. 17(1989), 191–196. http://dx.doi.org/10.1007/BF00401584 Google Scholar
[8] Favorov, S., Bohr and Besicovitch almost periodic discrete sets and quasicrystals. Proc. Amer. Math. Soc. 140(2012), 1761–1767. math.MG/1011.4036 http://dx.doi.org/10.1090/S0002-9939-2011-11046-3 Google Scholar
[9] Hof, A., On diffraction by aperiodic structures. Comm. Math. Phys. 169(1995), 25–43. http://dx.doi.org/10.1007/BF02101595 Google Scholar
[10] Hof, A., Diffraction by aperiodic structures. In: The mathematics of long-range aperiodic order, Kluwer, Dordrecht, 1997, 239–268.Google Scholar
[11] Kellendonk, J. and Lenz, D., Equicontinuous Delone Dynamical Systems. Canad. J. Math., to appear. math.DS/1105.3855 Google Scholar
[12] Gil., J. de Lamadrid, and Argabright, L. N., Almost periodic measures. Mem. Amer. Math. Soc. 85, 1990.Google Scholar
[13] Lagarias, J., Meyer's concept of quasicrystal and quasiregular sets. Comm. Math. Phys. 179(1996), 365–376. http://dx.doi.org/10.1007/BF02102593 Google Scholar
[14] Lagarias, J., Mathematical quasicrystals and the problem of diffraction. In: Directions in Mathematical Quasicrystals, CRM Monograph Series 13, Amer. Math. Soc., Providence, RI, 2000, 61–93.Google Scholar
[15] Lenz, D., Continuity of eigenfunctions of uniquely ergodic dynamical systems and intensity of Bragg peaks. Comm. Math. Phys. 287(2009), 225–258. math.PH/0608026 http://dx.doi.org/10.1007/s00220-008-0594-2 Google Scholar
[16] Lenz, D. and Richard, C., Pure Point Diffraction and Cut and Project Schemes for Measures: the Smooth Case. Math. Z. 256(2007), 347–378. math.DS/0603453 http://dx.doi.org/10.1007/s00209-006-0077-0Google Scholar
[17] Lenz, D. and Strungaru, N., Pure point spectrum for measurable dynamical systems on locally compact Abelian groups. J. Math. Pure Appl. 92(2009), 323–341. math-ph/0704.2498v2 Google Scholar
[18] Meyer, Y., Algebraic numbers and harmonic analysis. North-Holland, Amsterdam, 1972.Google Scholar
[19] Moody, R. V., Meyer sets and their duals. In: The mathematics of long-range aperiodic order (Waterloo, ON, 1995), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 489, Kluwer, Dordrecht, 1997, 403–441.Google Scholar
[20] Moody, R. V. and Strungaru, N., Point sets and dynamical systems in the autocorrelation topology. Canad. Math. Bull. 47(2004), 82–99. http://dx.doi.org/10.4153/Cmb-2004-010-8 Google Scholar
[21] Strungaru, N., Almost periodic measures and long-range order in Meyer sets. Discrete Comput. Geom. 33(2005), 483–505. http://dx.doi.org/10.1007/s00454-004-1156-9 Google Scholar
[22] Shechtman, D., Blech, I., Gratias, D. and Cahn, J.W., Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 53(1984), 1951–1953.Google Scholar