Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-23T18:55:20.138Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Asymptotic Behavior of Complete Kähler Metrics of Positive Ricci Curvature

Part of: Holomorphic functions of several complex variables Global differential geometry

Published online by Cambridge University Press:  20 November 2018

Boudjemâa Anchouche
Boudjemâa Anchouche*
Affiliation:
Sultan Qaboos University, Oman, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 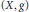$\left( X,\,g \right)$ be a complete noncompact Kähler manifold, of dimension 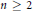$n\,\ge \,2$, with positive Ricci curvature and of standard type (see the definition below). N. Mok proved that $X$ can be compactified, i.e., $X$ is biholomorphic to a quasi-projective variety. The aim of this paper is to prove that the 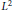${{L}^{2}}$ holomorphic sections of the line bundle 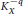$K_{X}^{-q}$ and the volume form of the metric $g$ have no essential singularities near the divisor at infinity. As a consequence we obtain a comparison between the volume forms of the Kähler metric $g$ and of the Fubini-Study metric induced on $X$. 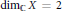In the case of ${{\dim}_{\mathbb{C}}}\,X\,=\,2$, we establish a relation between the number of components of the divisor 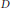$D$ and the dimension of the 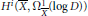${{H}^{i}}(\bar{X},\,\Omega \frac{1}{X}(\log \,D))$.

MSC classification

Secondary: 53C55: Hermitian and Kählerian manifolds 32A10: Holomorphic functions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 1 , 01 February 2010 , pp. 3 - 18
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] B., Anchouche, Sur la dimension logarithmique de Kodaira des variétés Kählériennes complètes de courbure de Ricci positive.Math Z. 227(1998), no. 3, 403-421. doi:10.1007/PL00004381Google Scholar
[2] P., Deligne, Théorie de Hodge. II. Inst. Hautes ´Etudes Sci. Publ. Math. (1971) No. 40, 5-57.Google Scholar
[3] N., Mok, An embedding theorem of complete Kähler manifolds of positive bisectional curvature onto affine algebraic varieties. Bull. Soc. Math. France 112(1984), no. 2, 197-258. ).Google Scholar
[4] N., Mok, An embedding theorem of complete Kähler manifolds of positive Ricci curvature onto quasi-projective varieties.Math. Ann. 286(1990), no. 1-3, 373-408. doi:10.1007/BF01453581Google Scholar
[5] N., Mok, Y. T., Siu, and S. T., Yau, Poincaré-Lelong equation on complete Kähler manifolds. Compositio Math. 44(1981), no. 1-3, 183-218.Google Scholar
[6] N., Mok and J. Q., Zhong, Compactifying complete Kähler manifolds of finite topological type and bounded curvature. Ann. of Math. 129(1989), no. 3, 427-470. doi:10.2307/1971513Google Scholar
[7] Y. T., Siu, Analyticity of sets associated to Lelong numbers and the extension of closed positive currents. Invent. Math. 27, 53-156. doi:10.1007/BF01389965Google Scholar
[8] H., Skoda, Prolongement des courants, positifs, fermés, de masse finie. Invent. Math 66(1982), no. 3, 361-376. doi:10.1007/BF01389217Google Scholar
[9] S.-K., Yeung, Complete Kähler manifolds of positive Ricci curvature. Math. Z. 204(1990), no. 2, 187-208. doi:10.1007/BF02570867Google Scholar