Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T05:26:40.329Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Algebra of Multipliers

Published online by Cambridge University Press:  20 November 2018

Roshdi Khalil
Roshdi Khalil*
Affiliation:
Kuwait University, Kuwait
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A commutative Banach algebra is called symmetric if, regarded as a function algebra on its maximal ideal space, it is closed under complex conjugation. Varopoulos, [5], proved the asymmetry of the tensor algebra 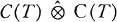, where T is the unit circle. It is the object of this paper to prove the asymmetry of the Schur multipliers of the space 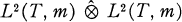, where m is the Lebesgue measure. In the second part of the paper we study the Hankel multipliers of the space 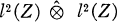and give an application to it.

1. The asymmetry of. Let C(T) denote the space of continuous functions on T and A(T) be the space of those functions in C(T) that have absolutely convergent Fourier series. Consider the mapping F: C(T) → C(T × T) defined by F(f)(x, y) = f (x + y).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 4 , 01 August 1981 , pp. 786 - 794
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Herz, C. S., Spectral synthesis for the cantor set, Proc. Natl. Acad. Sci. US 42 (1956), 42–43.Google Scholar
2. Katznelson, Y., An introduction to harmonic analysis, N.Y. (1968).Google Scholar
3. Khalil, R., Ph.D. Thesis (1978).Google Scholar
4. Rudin, W., Fourier-Stielljes transforms on independent sets, Bull. Amer. Math. Soc. 66 (1960), 199–202.Google Scholar
5. Varapoulos, N. Th., On a problem of A. Beading, J. Fun. Anal. 2 (1968), 24–30.Google Scholar
6. Varapoulos, N. Th., Tensor algebra over discrete spaces, J. Fun. Anal. 3 (1968), 321–335.Google Scholar
7. Williamson, J. H., A theorem on algebras of measures on topological groups, Proc. Edinburgh Math. Soc. 11 (1959), 195–206.Google Scholar